【信号与系统】Multisim 仿真连续时间系统的时域分析
Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: AXYZdong的博客
8小时Python零基础轻松入门
Multisim 14 仿真
文章目录
- 一. 实验目的
- 二. 实验原理
- 1. 状态轨迹简介
- 2. R,L,C的电压电流关系
- 3. 求解状态方程
- 4. 不同阻尼下的状态轨迹
- 5. 实验原理图
- 三. 仿真结果
- 四. 总结
一. 实验目的
- 观测连续时间系统的时域分析。
- 研究二阶串联电路的阶跃响应。
- 观测更改参数对于连续系统的阶跃响应的影响。
- 观测系统的状态轨迹的显示。
二. 实验原理
1. 状态轨迹简介
1、 任何变化的物理过程在第一时刻所处的 “状态”(状况、形态或姿态),都可以用若干被称为“状态变量”的物理量来描述。电路也不例外,若一个含储能元件的网络在不同时刻各支路电压、电流都在变化,那么电路在不同时刻所处的状态也不相同。
2、 对 n 阶网络可以用n个状态变量来描述。可以设想一个 n 维空间,每一维表示一个状态变量,构成一个“状态空间”。网络在每一时刻所处的状态可以用状态空间中一个点来表达,随着时间的变化,点的移动形成一个轨迹,称为“状态轨迹”。二阶网络的状态空间就是一个平面,状态轨迹是平面上的一条曲线。一个 n 阶系统,只能有 n 个状态变量,不能多也不可少,且 n 个状态变量间线性无关的。
3、 为便于用双踪示波器直接观察到网络的状态轨迹,本实验仅研究 RLC 串联电路构成的二阶网络,它的状态轨迹可在二维状态平面上表示。
2. R,L,C的电压电流关系
→ { i R = u R R u R = i R ⋅ R \to \begin{cases} i_R=\frac{u_R}{R}\\ \\ u_R=i_R\cdot R \end{cases} →⎩⎪⎨⎪⎧iR=RuRuR=iR⋅R
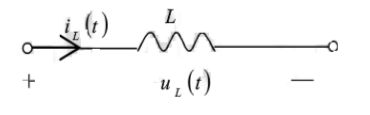
→ { u L ( t ) = L d i L ( t ) d t i L ( t ) = 1 L ∫ − ∞ t u L ( τ ) d τ \to \begin{cases} u_L(t)=L\frac{di_L(t)}{dt}\\ \\ i_L(t)=\frac{1}{L}\int_{-\infty}^{t}u_L(\tau)d\tau \end{cases} →⎩⎪⎨⎪⎧uL(t)=LdtdiL(t)iL(t)=L1∫−∞tuL(τ)dτ
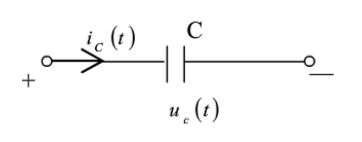
→ { i C ( t ) = C d u C ( t ) d t u C ( t ) = ∫ − ∞ t i C ( τ ) d τ \to \begin{cases} i_C(t)=C\frac{du_C(t)}{dt}\\ \\ u_C(t)= \int_{-\infty}^{t}i_C(\tau)d\tau \end{cases} →⎩⎪⎨⎪⎧iC(t)=CdtduC(t)uC(t)=∫−∞tiC(τ)dτ
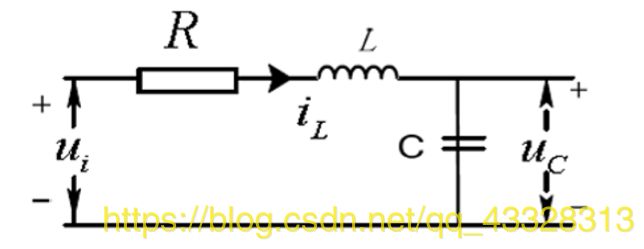
▲ RLC串联电路
插播一条反爬虫信息,读者可以忽略:
3. 求解状态方程
如图所示的RLC串联电路,选取 i L i_L iL 和 u C u_C uC 为中间状态, u C u_C uC 为输出, u i u_i ui 为输入。根据电压关系,
i L R + L d i L d t + u c = u i (1) i_LR+L\frac{di_L}{dt}+u_c=u_i \tag1 iLR+LdtdiL+uc=ui(1)
求得相应的微分方程(状态方程)为:
→ { u c ′ = 1 C i L i L ′ = − 1 L u c − R L i L + 1 L u i (2) \to \begin{cases} u'_c=\frac{1}{C}i_L\tag 2\\ \\ i'_L=-\frac{1}{L}u_c-\frac{R}{L}i_L+\frac{1}{L}u_i \end{cases} →⎩⎪⎨⎪⎧uc′=C1iLiL′=−L1uc−LRiL+L1ui(2)
由(2) 式不难看出,当已知电路的激励电压ui和初始条件 i L ( t 0 ) i_L(t_0) iL(t0)、 u c ( t 0 ) u_c(t_0) uc(t0),就可以唯一地确定 t ≥ t 0 t≥t_0 t≥t0 时,该电路的电流和电容两端的电压 u c u_c uc。
将 i C ( t ) = C d u C ( t ) d t i_C(t)=C\frac{du_C(t)}{dt} iC(t)=CdtduC(t) 带入(1)式,相应的输入输出之间的关系:
L C d 2 u c d t 2 + R C d u c d t + u c = u i (3) LC\frac{d^2u_c}{dt^2}+RC\frac{du_c}{dt}+u_c=u_i\tag 3 LCdt2d2uc+RCdtduc+uc=ui(3)
根据(3)式整理得:
d 2 u c d t 2 + R L d u c d t + 1 L C u c = 1 L C u i (4) \frac{d^2u_c}{dt^2}+\frac{R}{L}\frac{du_c}{dt}+\frac{1}{LC}u_c=\frac{1}{LC}u_i\tag 4 dt2d2uc+LRdtduc+LC1uc=LC1ui(4)
二阶网络标准化形成的微分方程为
d 2 u c d t 2 + 2 ξ ω n d u c d t + ω n 2 u c = ω n 2 u i (5) \frac{d^2u_c}{dt^2}+2\xi\omega_n\frac{du_c}{dt}+\omega^2_nu_c=\omega^2_nu_i\tag 5 dt2d2uc+2ξωndtduc+ωn2uc=ωn2ui(5)
其中 ξ ξ ξ 称为阻尼比, ω \omega ω 称为无阻尼自振角频率。
比较(4)式和(5)式,得
ω n = 1 L C ξ = R 2 C L (6) \omega_n=\frac{1}{\sqrt{LC}} \\ ξ=\frac{R}{2}\sqrt{\frac{C}{L}}\tag 6 ωn=LC1ξ=2RLC(6)
由(6)式可知,改变 R 、 L 和 C R、L和C R、L和C ,使电路分别处于 ξ = 0 、 0 < ξ < 1 和 ξ > 1 ξ=0、0<ξ<1 和 ξ>1 ξ=0、0<ξ<1和ξ>1 三种状态。根据(3)式,可直接解得 u C ( t ) u_C(t) uC(t) 和 i L ( t ) i_L(t) iL(t) 。如果以 t t t 为参变量,求出 i L = f ( u C ) i_L=f( u_C) iL=f(uC) 的关系,并把这个关系,画在 u C − i L ( t ) u_C-i_L(t) uC−iL(t) 平面上。显然,后者同样能描述电路的运动情况。
4. 不同阻尼下的状态轨迹
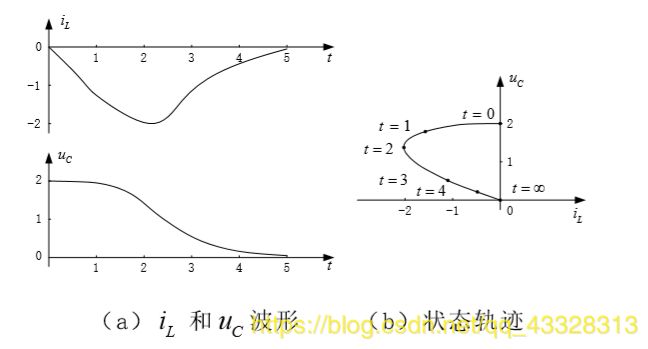
▲ RLC电路在过阻尼时的状态轨迹
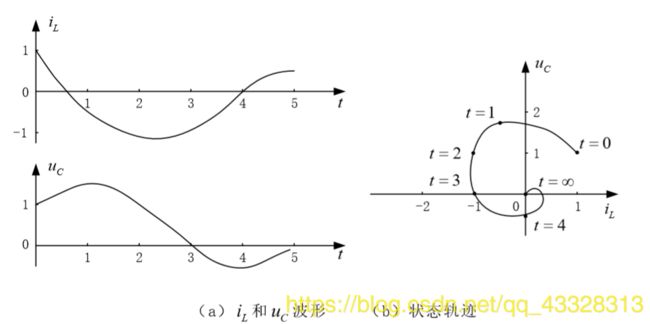
▲ RLC电路在欠阻尼时的状态轨迹
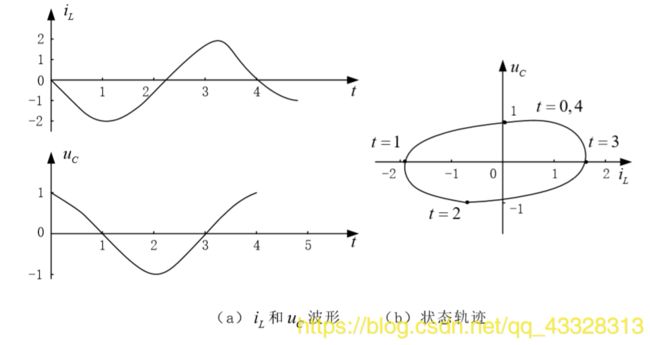
▲ RLC电路在R=0时的状态轨迹
- 李沙育图是电压电流瞬时相互关系的图形表示,即状态轨迹。如果电压电流同是正弦,图是椭圆,长轴和水平轴之间的夹角就是电压电流差角。
5. 实验原理图
-
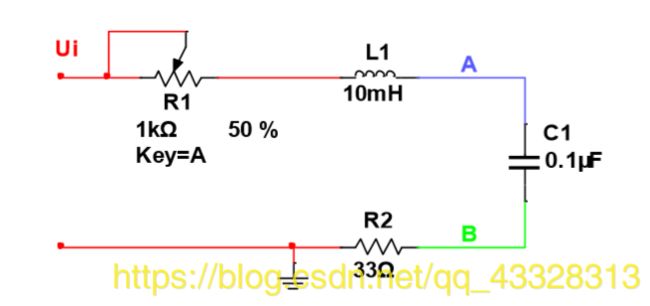
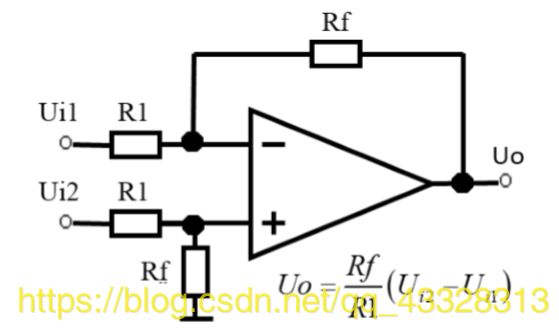
实验原理线路如图所示, R = R 1 + R 2 = R 1 + 33 Ω R=R1+R2=R1+33Ω R=R1+R2=R1+33Ω,改变 R 1 R1 R1 也就改变了 R R R 的值, ξ ξ ξ 值也会改变,从而使电路处于过阻尼、欠阻尼和临界阻尼的状态。为了便于测量, R 2 R2 R2 两端的电压和 i L i_L iL 成正比,只要将 U R 2 U_{R_2} UR2 和 U C U_C UC 加到示波器的两个输入端,其李萨如图形即为该电路的状态轨迹。但示波器的两个输入必须有一个共地端,而 U R 2 U_{R_2} UR2 和 U C U_C UC 没有共地端,因此必须将 (A点和B点)通过如图 的减法器(取 R 1 = R f R1=Rf R1=Rf ),将双端输入的 U C U_C UC 变为与 U R U_{R } UR 一个公共端的单端输出。这样,电容两端的电压 U R U_{R } UR 和 U C U_C UC 有一个公共接地端,从而能正确地观察该电路的状态轨迹。
-
在本实验中,观察状态轨迹采用简易方法,由于 R 2 R2 R2 阻值很小,在B点电压仍表现为容性,因此电容电压可看成A和GND之间的电压。实验箱一般都是采用这种近似方法。
▲ Multisim 图
▲ 减法器电路
三. 仿真结果
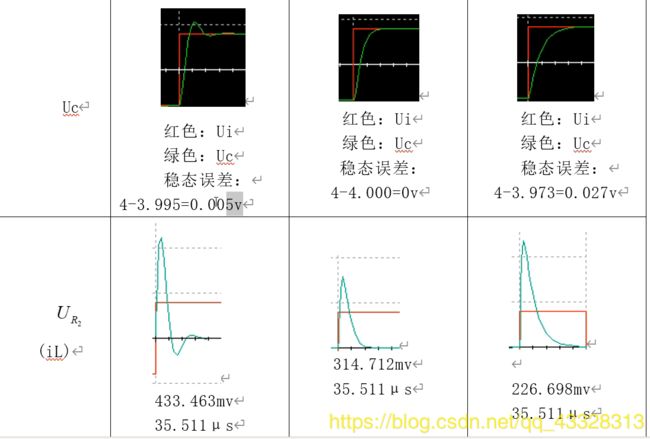
▲ Ui 和 iL波形
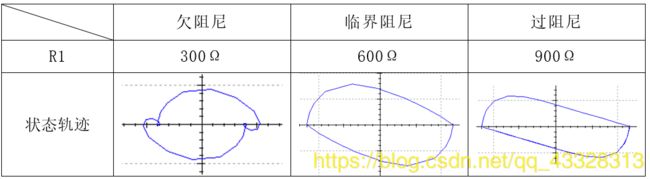
▲ 状态轨迹
四. 总结
- 临界阻尼的计算
- 输入信号的选择:幅度 4 V 4V 4V、频率 f = 1 K H z f=1KHz f=1KHz 、占空比50%的方波
- 显示李萨如图形:示波器工作模式选择
A/B
本次的分享就到这里
![]()
好书不厌百回读,熟读自知其中意。将学习成为习惯,用知识改变命运,用博客见证成长,用行动证明努力。
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “评论” “收藏” 一键三连哦!
听说 点赞 的人运气不会太差,每一天都会元气满满呦!^ _ ^ ❤️ ❤️ ❤️
码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了关注我哦!
更多精彩内容请前往 AXYZdong的博客
如果以上内容有任何错误或者不准确的地方,欢迎在下面留个言。或者你有更好的想法,欢迎一起交流学习~~~