卷积神经网络之快速卷积算法(img2col、Winograd、FFT)

前言

最近几天尝试着不用框架写一个卷积神经网络，后来代码写完之后发现运行的速度实在是太慢，分析了一下发现主要的时间都花在了卷积层上。于是查找各种资料，学习了两种现在主流的快速卷积算法，写此文主要记录一下其中的要点，在学习过程中遇到的问题。

FFT

如果学过或者了解过信号的，你肯定肯定，空间域中矩阵的卷积运算，实际上等价于频率域中两个矩阵对应元素相乘，关于怎么进行快速傅里叶变换,我之前的文章已经讲述过了，对这块不太了解的，可以点击这里。

不过问题主要是，通常情况下，我们的feature的尺寸要比卷积核的尺寸大得多，如果直接对两者进行快速傅里叶变换的话，那么得出来的两个矩阵大小不一样，不能进行对应位置相乘。

因为为了可以让他们对应位置进行相乘，我们就必须要对卷积核进行扩充，将其扩充到与feature尺寸大小相同。然而也正是这个扩充过程，限制了这种方法的使用。所以只有在卷积核和feature尺寸大小差不多的时候，我们才会使用这种方法。

下面来说明下，怎么进行扩充，以及需要注意的地方

通常情况有三种卷积方式full、same、valid,

下面三幅图就描述的很清楚（图片来源）

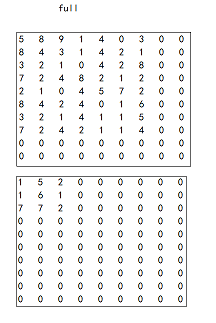
full卷积方式如下图，这种卷积方式会先对图像的四周进行补零，补零的行数(列)为卷积核宽度(长度)-1,最终卷积出来的结果一定会比原图像大的

---

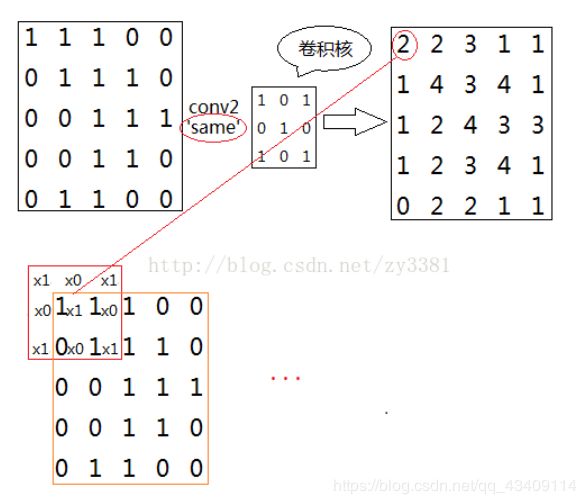
same卷积方式如下图所示，这种方式卷积结果大小一定会与原图像大小一样，通常补零的个数为
向下取整(卷积核大小/2)。

---

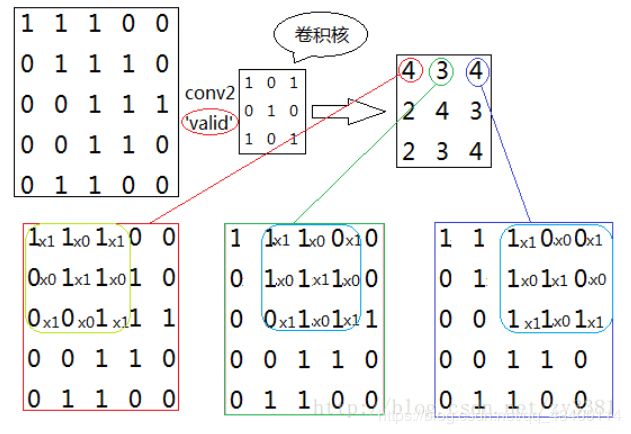
valid卷积方式如下图所示，如果用这种方式进行卷积我们不会对原图像进行补零操作，所以会导致原图像变小

现在我们来分析一下，如果使用FFT来进行快速卷积，该怎么补零

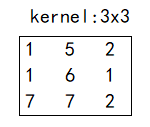
假设，我们的输入的图像和卷积核分别如下图所示。

1. 如果采用full方式进行卷积，则补零应该如下
   
   (上为输入，下为卷积核)
   这是因为，在用full方式进行卷积的时候，原图8x7大小，会变成10x9的大小，所以我们要把原图填充成上述样子。同理，我们需要把卷积核进行填充至10x9的大小

2. 如果采用same方式或则采用valid方式进行卷积，上面的补零方式就不管用，我这边也没有发现为啥不管用，后续我会在研究研究。

你以为补完零就结束了吗？不，还没有！
在图像处理领域和深度学习领域中定义的卷积运算和信号和数学领域中定义的卷积运算是不同的，是由一些差异的，具体的数学可以看《深度学习》中P283页。这里我只讲述一下这两则的差异。

在数学领域中，对于二维的卷积,如下图[图片来源]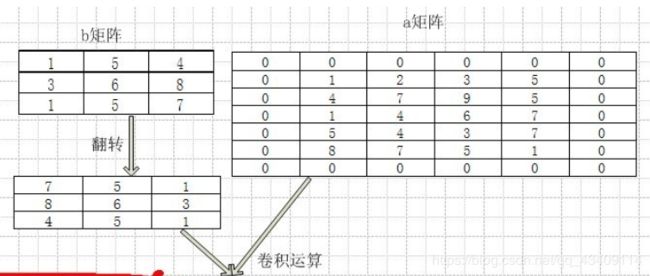
也就是说，我们需要先对其进行一次水平翻转和垂直翻转，然后在进行计算机领域所谓的卷积运算。

所以对feature和核填充零之后，还需对核进行一次水平翻转核垂直翻转

代码实现

def fftConvt(img,ker):
    # 第一步，对img进行填充
    img_padding=np.zeros(shape=[len(img)+len(ker)-1,len(img)+len(ker)-1])
    img_padding[len(ker)-1:len(ker)-1+len(img),len(ker[0])-1:len(ker[0])-1+len(img[0])]=img
    ker=np.flip(ker,axis=0)
    ker = np.flip(ker, axis=1)
    # 第二步，对卷积核进行填充
    ker_padding=np.zeros(shape=img_padding.shape)
    ker_padding[:len(ker),:len(ker[0])]=ker
    img_padding_fft2=np.fft.fft2(img_padding)
    ker_padding_fft2=np.fft.fft2(ker_padding)
    img_fft2=img_padding_fft2*ker_padding_fft2
    return np.real(np.fft.ifft2(img_fft2))

img2col

这个算法原理挺简单的，就是将卷积运算，转换为矩阵乘法运算。因为现在线性代数领域已经有非常成熟的计算矩阵乘法，几乎可以做到极限优化。

整个算法流程大概如下
参考：High Performance Convolutional Neural Networks for Document Processing

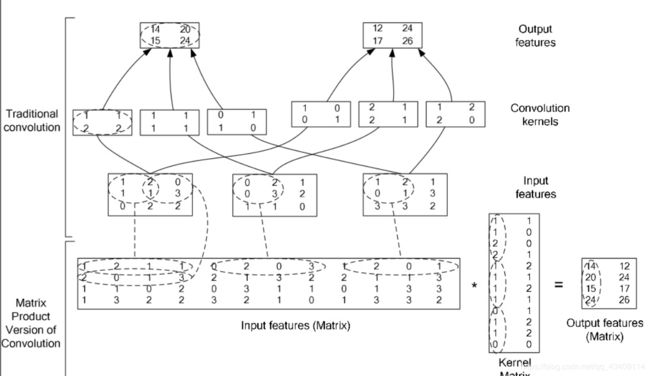
我第一次看上面这个图，看的我一脸懵逼，现在来逐一分析一下。上述流程图中，输入的数据是一个三通道的features，如下

我们有2个卷积核，每个卷积核有三个子核，如下

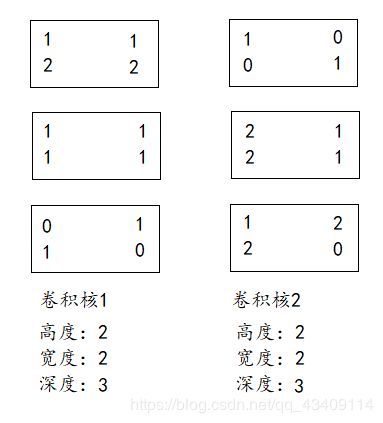
那么怎么样把卷积运算给转换成矩阵乘法呢？

想象一下，在进行传统卷积的时，我们会移动滑块，然后对滑块进行加权求和。现在我们要做的是,将每个滑块形成的子矩阵给拉直，假设我们拿出features中的第一个通道的数据，如下

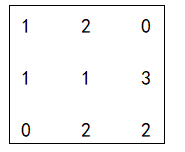
在拿出第一个卷积核中的第一个子矩阵

现在我们移动滑动窗口，逐一的把滑动窗口选中的部分给拉直，如下图所示

然后就形成了四个向量，现在我们要做的就是把这四个向量给堆叠起来，形成一个新的矩阵，如下

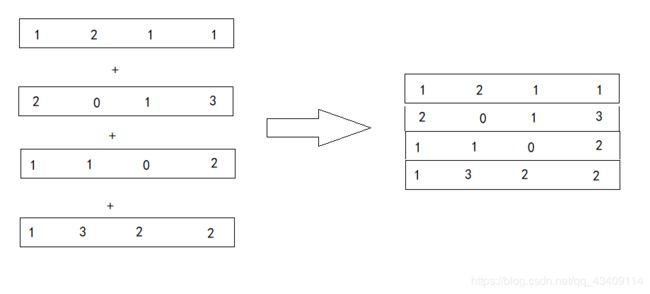
完成上述步骤之后，在把卷积核给拉直，如下

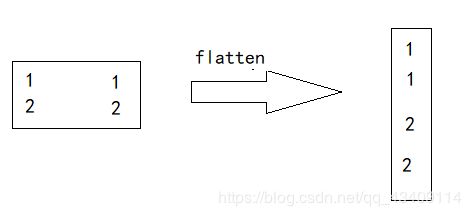
现在，我们就可以用之前形成的矩阵和这个列向量进行矩阵乘法运算

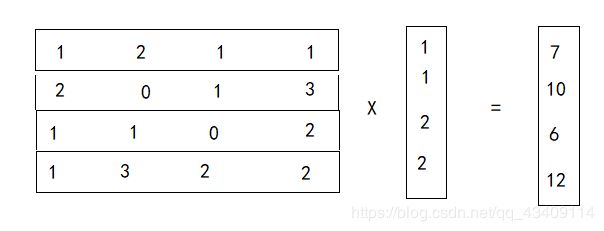
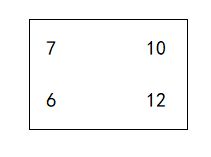
做乘法之后，会得到一个列向量，这个列向量中的每个元素就是每个窗中加权平均值，即卷积值，因为4x4矩阵 做 2x2的卷积，输出是2x2，所以我们在将这个列向量reshape一下，即可得到最终结果

上述过程只是单通道情况下，所以对于多通道，我们就可以把三个通道生成的矩阵给堆叠在一起，如下图

每个卷积核的子矩阵给拉直，然后再堆叠到一起,如下图

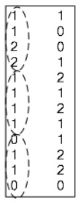
最后计算两者的乘积，即可得到最终的卷积结果。

代码实现

def img2col(img,ker):
    ker_width=len(ker[0])
    ker_height=len(ker)
    transform=np.empty(shape=((len(img[0]) - ker_width)*(len(img) - ker_height), ker_width*ker_height))
    cur=0
    for y in range(0,len(img)-ker_height):
        for x in range(0, len(img[0]) - ker_width):
            data=img[y:y+ker_height,x:x+ker_width].reshape(1,9)
            transform[cur,:]=data
            cur=cur+1
    return np.dot(transform,ker.reshape(-1,1)).reshape(len(img)-ker_height,-1)

Winograd

Winograd算法出自CVPR 2016的一篇 paper：Fast Algorithms for Convolutional Neural Networks。，这个算法可以用来加速卷积运算，目前有很多框架如NCNN、NNPACK等，对于卷积层都采用了Winograd快速卷积算法。

对于这个算法的讲解，网上还是不少资料可以查到的，在这里我推荐几篇

1.Fast Algorithms for Convolutional Neural Networks 直接啃原论文

2 卷积神经网络中的Winograd快速卷积算法

在这里，我只想记录一下，学习这个算法的过程中遇到的问题

1. 对于一维情况， F(2, 3)是用来解决kernel长度为3，输出为2的卷积问题，说白了就是只能解决输入长度为4，输出长度为2，kernel为3的问题，那么如果我想要解决输入为n，输出为m，kernel为3的问题，那我是不是得构建一个F(m,3)?

答：完全不需要，虽然说，F(2,3)只能用来计算输入长度为4，卷积核为3的情况，但是如果我们如果有n个数据，我们完全可以将这n个数据划分成若干组，每组长度为4,然后分别对每组进行卷积运算，最后将所有组得出的结果，堆叠在一起即可，这里的组，也就是tile

2. 对于二维情况，公式如下，其中g是什么？d又是什么?
   $$Y=A^T[[Gg{G}^T]\odot [B^{T}dB]]A$$

答：这里的g就是kernel,不需要做任何改变不需要做任何调整。这里的d就是tile。

代码实现如下：

def Winograd(img,ker):
    U = G.dot(ker).dot(G.T)
    res=np.empty(shape=[98,98])
    for y in range(0,len(img)-8,6):
        for x in range(0, len(img[0])-8,6):
            tile=img[y:y+8,x:x+8]
            V=BT.dot(tile.T).dot(BT.T)
            res[y:y+6,x:x+6]=AT.dot(U*V).dot(AT.T).T
    return res

不过，好像运行的并不是很快。。。。。。。希望有大佬能够指点

关于转换矩阵的推导，需要用到数论，整个过程十分复杂，如果想了解的，可以看此文章，文章篇目十分长，我看了一整天才勉勉强强弄明白

1. Winograd变换矩阵生成原理

\