字符串匹配算法
朴素思想(暴力)
任何一种问题,我们都习惯先写出暴力做法,然后再去想如何优化。对于字符串匹配也是如此,话不多说,直接上代码,暴力遍历比较。
for (int i = 0; i < n; i ++ )
{
bool flag = true;
for (int j = 0; j < n-m+1; j ++ )
{
if (text[i + j ] != pattern[j])
{
flag=false;
break;
}
}
if(flag)
return i;
}
虽然说暴力做法一直是效率低下的代言词,但对于平常使用来说,这种做法就已经够用了。因为在实际开发中,大部分情况下的主串和模式串的长度都不会太长。并且它思路清晰简单,出问题也好修复。实际上一般 string 的查找函数就是这种做法。
但是也不能就会这一招就阿尼陀佛,万事大吉了。总有需要优化的时候,计算机之所以在现代社会有着举足轻重的地位,就在于人在不断思考,并优化它的执行方式。缺少了人的思考,它只是一坨笨的不能再笨的铁而已。
KMP
朴素做法虽然简单,但主串与模式串的指针都要来回移动。我们去书上找东西一般都是一眼扫过去,有没有什么办法可以让主串的指针不往回走,降低比较的趟数?
在上面这个例子中,很明显更快的做法是在第一次匹配失败之后,跳过第二次匹配,进行第三次匹配。也就是说,应该向后移动两格而不是一格。KMP的思想就在于利用已知信息,不把"搜索位置"移回已经比较过的位置,继续向后移。
我们可以利用模式串自身的特点,利用已经匹配过的结果来减少枚举过程,跳过不可能成功的比较,加速匹配过程。画个抽象点的图:
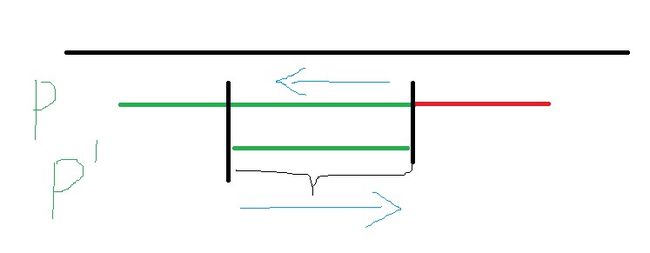
在主串指针不往后退的前提下, 我们的模式串指针最多回退到哪里就可以继续进行匹配呢?
如上图,回退之后的字符串肯定是要能与主串匹配成功的。也就是说它与之前的模式串有着交集。从图中可以看到,P串的后缀与P'的前缀相同。那个这个问题:在已有N个匹配成功的结果下,第N+1个字符匹配失败时,模式串应该退回到第?个匹配成功的结果下?也就转换成了:模式串的各个字串中,能使前后缀相等的最大长度是多少?
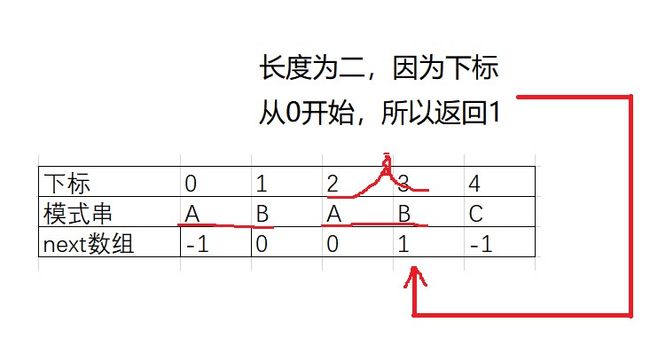
我们用next数组来存储回退到的下标
虽然说1那里应该等于0,但其实这时候已经退无可退了。所以应该退出循环,让主串指针向前走一位,开始新一轮比较。
利用这个next数组,比如我们比较到下标3的时候发现不匹配,没关系,我们退一步。退一步之后就到了下标1(回退看的next应该是已经匹配成功的那个,也就是看下标2存的是几),如果这时候还不匹配,那我们就会退回到-1,也就是说,这轮匹配失败了,主串可以往前走了。
看看代码就清楚了
int strStr(string haystack, string needle)
{
if (!needle.size()) return 0;
if (!haystack.size()) return -1;
vector next(needle.size());
next[0] = -1;
//求next数组
for (int i = 1, j = -1; i < needle.size(); i++)
{
while (j >= 0 && needle[i]!=needle[j+1])
{
//不匹配就退一步看看
j = next[j];
}
if (needle[i] == needle[j + 1])
{
//匹配成功就继续往后走
//看看还能不能匹配成功
j++;
}
next[i] = j;
}
//开始匹配
for (int i = 0, j = -1; i < haystack.size(); i++)
{
while (j != -1 && haystack[i] != needle[j+1])
{
//不匹配咱就回退
j = next[j];
}
if (haystack[i] == needle[j+1])
{
j++;
}
if (j == needle.size() - 1)
{
return i-j;
}
}
return -1;
}
BM
虽然KMP比较出名,但其实只是因为它比较难懂而已。在效率上有很多的算法都比它要好。现在介绍的BM算法,其效率就要比KMP好上3到4倍。
BM算法包含两部分:坏字符规则和好后缀规则
坏字符规则
BM算法与我们平常接触的字符串比较方法不同,它是按模式串从大到小的顺序,倒着比的。这样做也是有好处的,起码直观上是这样感觉的。就像做算数选择题,出卷老师为了让你花的时间久一点,故意把正确答案放到C跟D上。所以聪明点的做法应该是先算C跟D。这跟这个比较方法有点类似。
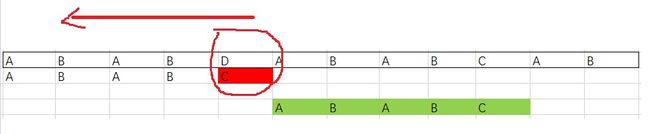
考虑下面这张图:
别忘了我们是从模式串最大的开始往后匹配,所以这里先比较了C和D。这个时候,有意思的来了,这个 D 在模式串中就没有出现过,是一个坏字符,有它在的字串可能不匹配。
惹不起还躲不起吗?溜之大吉,模式串直接移动五位,重新匹配。一下移动这么多,是不是特别的爽?
但你千万不要以为只有没在模式串中出现过的才叫坏字符,实际上这个只是从后往前第一个不匹配的字符。一旦发生不匹配,坏字符规则的做法是模式串指针继续往回走,找到第一个与其匹配的字符停止,然后再继续新一轮的匹配。
也就是说,移动的距离等于:当前模式串的下标(Si) - 往回走找到的第一个与当前不匹配字符匹配的下标(Xi)。如果没有找到,则减数为-1。
这么一想,好像用坏字符规则就万事大吉了。但因为实际代码中,我们不会每次不匹配都会往前找,那样太耗费时间,取而代之的是使用散列表纪录不同字符在模式串中“最后出现的位置”,并不是 Si 的位置往前查找的第一个位置,所以可能会出现 Xi 大于 Si 的情况。比如上图的例子,主串"ABABDABABCAB",模式串"ABABC"当从左开始数的一个B不匹配时,找到的A的下标是最后一次在模式串中出现的下标(也就是最后一个a的位置,比A大)。这时候,模式串非但不往前滑动,还回退了。为了解决这个问题,我们需要好后缀来帮忙。(实际上,两个规则都可以独立使用,如果坏字符你是往回遍历而不是保存在散列表里面的话)
好后缀规则
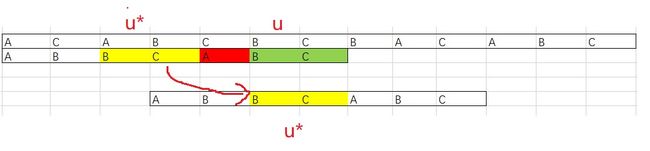
当遇到上图的情况时,我们依然可以用坏字符规则来移动,但这次让我们来看看好后缀是如何工作的?
我们把在主串中已经匹配成功的字符串用 u标记,现在要做的是找到模式串中与其匹配的u*如果找到了,那模式串就滑动到使得u*与u对齐的位置。如果不匹配,那么溜之大吉,直接移动一个模式串长度的位置。虽然一次移动那么多是很爽,但这样做有可能错过可以匹配的情况。
实际上这里应该跟KMP一样,如果模式串中前缀与好后缀的后缀相同,那么就移动相应位置使其匹配。
双剑合璧
两个规则你都知道了,并且他们都可以独立使用,那么到底该选哪一个呢?
可以参考的建议
- 如果处理的是字符集很大的字符串匹配问题,那么坏字符规则对内存的消耗会比较多。因为两个规则是独立的,所以可以考虑仅使用好后缀
- 如果同时使用两个规则,滑动的大小应该是两个规则中最大的那一个,这样可以避免负数的产生
代码实现
如前面所说,坏字符如果每次都在模式串中遍历的话,会对性能造成影响。那么有没有什么高效的办法代替遍历呢?
我们可以将模式串中的每个字符及其下标都存到散列表中,这样就能快速的找到坏字符在模式串的对应下标了。
先打好坏字符规则
private:
static const int SIZE = 256;
//求bc
vector getBC(string pattern)
{
vector bc(SIZE,-1);
for (int i = 0; i < pattern.size(); i++)
{
int ascii = (int)pattern[i];
bc[ascii] = i;
}
return bc;
}
int strStr(string haystack, string needle)
{
if (needle.size() == 0) return 0;
vector bc(SIZE);
bc = getBC(needle);
int i = 0;
while (i <= haystack.size() - needle.size())
{
int j;
//别忘了,BM是从后往前匹配哦
for (j = needle.size() - 1; j >= 0; j--)
{
//不等于咱就要去找滑动位置了
if (haystack[i + j] != needle[j])
break;
}
if (j < 0)
{
//这是匹配成功!我们是从后往前的!!!
return i;
}
//找到模式串中最近的坏字符
i = i + j - bc[(int)haystack[i + j]];
}
return -1;
}
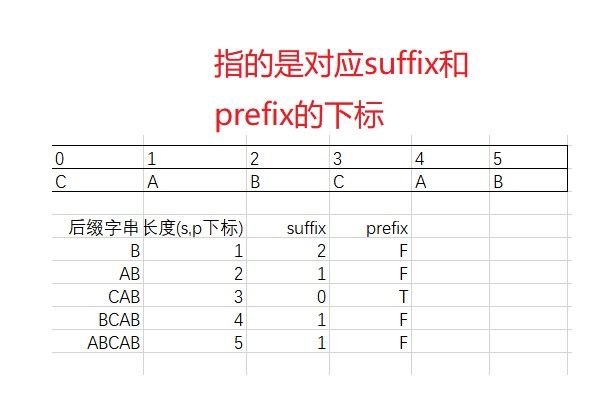
好后缀稍微麻烦一点,与KMP类似,我们用一个int数组suffix来保存。其下标表示后缀子串的长度。让我们来明确一下要干的事:在好后缀的后缀子串中,查找最长的、能跟模式串前缀子串匹配的后缀子串。所以存储的应该是在模式串中跟好后缀u相匹配的子串u*的起始下标值。
等等!我们好像漏了什么?在模式串中查找跟好后缀匹配的另一个子串,并且在好后缀的后缀子串中,查找最长能跟模式串前缀子串匹配的后缀子串。
suffix数组只能完成前半段话,那前缀子串的问题该如何解决呢?我们只能是再开一个bool数组prefix 来做这件事了。
求这两个数组的方法也十分讨巧,纪录公共后缀子串u*的起始下标为j,如果j==0,说明是前缀字串(因为已经走到尽头了),prefix为true。代码实现是下面这样:
//好后缀
void genGS(string pattern)
{
int len = pattern.size();
for (int i = 0; i < len; i++)
{
suffix.push_back(-1);
prefix.push_back(false);
}
for (int i = 0; i < len - 1; i++)
{
int j = i;
//公共后缀u*的长度
int k = 0;
while (j >= 0 && pattern[j] == pattern[len - 1 - k])
{
j--;
k++;
//保存的是在pattern中的起始下标
suffix[k] = j + 1;
}
if (j == -1)
prefix[k] = true;
}
}
现在让我们来把两个规则一起用在字符串匹配上
private:
static const int SIZE = 256;
vector bc;
vector suffix;
vector prefix;
//坏字符
void getBC(string pattern)
{
for (int i = 0; i < SIZE; i++)
{
bc.push_back(-1);
}
for (int i = 0; i < pattern.size(); i++)
{
int ascii = (int)pattern[i];
bc[ascii] = i;
}
}
//好后缀
void genGS(string pattern)
{
int len = pattern.size();
for (int i = 0; i < len; i++)
{
suffix.push_back(-1);
prefix.push_back(false);
}
for (int i = 0; i < len - 1; i++)
{
int j = i;
//公共后缀u*的长度
int k = 0;
while (j >= 0 && pattern[j] == pattern[len - 1 - k])
{
j--;
k++;
//保存的是在pattern中的起始下标
suffix[k] = j + 1;
}
if (j == -1)
prefix[k] = true;
}
}
int moveByGS(int j, int len)
{
//好后缀长度
int k = len - 1 - j;
if (suffix[k] != -1)
return j - suffix[k] + 1;
for (int i = j + 2; i < len; i++)
{
if (prefix[len = i])
return i;
}
return len;
}
int strStr(string haystack, string needle)
{
if (needle.size() == 0) return 0;
getBC(needle);
genGS(needle);
int i = 0;
while (i <= haystack.size() - needle.size())
{
int j;
//别忘了,BM是从后往前匹配哦
for (j = needle.size() - 1; j >= 0; j--)
{
//不等于咱就要去找滑动位置了
if (haystack[i + j] != needle[j])
break;
}
if (j < 0)
{
//这是匹配成功!我们是从后往前的!!!
return i;
}
//找到模式串中最近的坏字符
int x = j - bc[(int)haystack[i + j]];
int y = 0;
//如果有好后缀
if (j < needle.size() - 1)
{
y = moveByGS(j,needle.size());
}
i = i + max(x, y);
}
return -1;
}