[基于Matlab的误码率仿真]-公式中Eb_N0等的Matlab表示求法

参考文献：Bit-Error-Rate Simulation Using Matlab
作者：James E. Gilley             August 19, 2003

在学习OFDM系统相关MATLAB仿真时，需要了解这方面内容，看到了这篇论文，但是在搜索出来的其他博客内容中用将Eb解释为符号能量，以至于我很迷惑。所以下载原文后，进行了内容翻译并在此记录，希望能对其他人有帮助。

理论知识比较好的，可以直接看代码

1.功率
假设我们有一个信号x（n），其中n是样本数的索引。我们将信号的瞬时功率定义为：

一个更有用的量是平均功率，也就是信号中每个样本瞬时功率的平均值。对于信号x（n），N个采样样本，我们有：

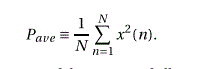
注意，这只是所有样本的平方和除以样本数。使用Matlab计算信号“x”的平均功率“pav”的一种方法是：

  Pav=sum(x.^2)/length(x);     

如果我们的信号平均值为零，或者换言之，没有直流分量，我们可以通过取其方差来求出信号的平均功率。这是因为：

σ(x)=E[x^2]− (E[x])^2,

信号的方差是其平方的平均值减去其平均值的平方。如果平均值为零，方差就是平方的平均值，与平均功率完全相同。因此，如果一个信号没有直流值，我们可以通过求其方差来计算其平均功率。我们需要小心使用方差来找到信号的平均功率。只有当信号的平均值为零时，这种技术才有效。

2.能量
从定义上讲，功率是能量的时间导数；或者说，能量是功率的时间积分。对于采样信号，积分变为求和。由于能量是功率和时间的乘积，信号的总能量必须等于其平均功率乘以其持续时间。此外，信号的持续时间是其采样长度除以采样频率，单位为每秒采样数。因此：

用于查找具有采样率“fs”的信号“x”的总能量“et”的Matlab命令为：

et=sum(x.^2)/fs.

3.建立信噪比
信噪比（SNR）Eb/N0通常用分贝表示，但在进一步利用信噪比之前，必须将分贝转换成一个普通的比值。如果我们把信噪比设为m分贝，那么Eb/N0=10^(m/10)
使用Matlab，我们从信噪比（单位为分贝）中找到比率“ebn0”，即：

ebn0=10^（Eb/N0_db/10）

注意Eb/n0是一个无量纲量。

4.确定Eb

每比特能量是信号的总能量，除以信号中包含的比特数。我们还可以将每比特的能量表示为平均信号功率乘以一比特的持续时间。Eb的表达式是：

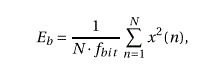
其中N是信号中的样本总数，fbit是比特每秒的比特率。
使用Matlab，我们可以找到传输信号“x”（具有比特率“fb”）的每比特能量“eb”，如下所示：

eb=sum(x.^2)/(length(x)∗fb).

5.计算N0
在信噪比和每比特能量已知的情况下，我们可以计算噪声的单侧功率谱密度N0。只要我们把信噪比从分贝转换成一个比率，我们所要做的就是用eb除以信噪比。
使用Matlab，我们得到噪声的功率谱密度“n0”，给定bit能量“eb”，和信噪比“ebn0”，分别为：

n0=eb/ebn0

6.计算σn
噪声的单侧功率谱密度N0告诉我们在信号的1.0hz带宽中存在多少噪声功率。为了找出噪声的方差或平均功率，我们必须知道噪声带宽。对于以fsHz采样的真实信号x（n），噪声带宽将是采样率的一半。因此，我们通过将噪声的功率谱密度乘以噪声带宽来计算噪声的平均功率：

σn=(N0·fs)/2

式中，σn为噪声方差，N0为噪声的单边功率谱密度。
使用Matlab，功率谱密度为“n0”、采样频率为“fs”的噪声的平均噪声功率“pn”计算如下：

pn=n0∗fs/2.

7.产生噪声
虽然Matlab的通讯工具箱有产生加性高斯白噪声的功能，但我们将使用一个标准的内置函数来产生AWGN。由于噪声的均值为零，其功率和方差是相同的。我们需要生成一个与信号向量x（n）长度相同的噪声向量，该噪声向量必须具有方差σn。
Matlab函数“randn”生成均值为零方差为1的正态分布随机数。我们必须缩放输出，使结果具有所需的方差σn。为此，我们只需将“randn”函数的输出乘以sqrt(σn)。我们可以生成噪声向量“n”，如下所示：

n=sqrt(pn)∗randn(1,length(x));.

8.确定偏移量
在接收比特和发送比特之间将存在偏移。在比较这两个位序列以检查错误之前，我们必须首先确定这个偏移量。种方法是将两个序列关联起来，然后搜索相关峰。
使用Matlab，我们可以从bit向量“tx”和“rx”创建一个部分互相关“cor”，循环如下：

for lag=1:length（rx）–length（tx）–1，
cor（lag）=tx*rx（lag:length（tx）–1+lag）'；
end

我们需要找到“cor”最大值的位置，因为这将告诉我们位向量之间的偏移量。由于Matlab将数组元素的数目定为1:N，而不是0:N-1，因此我们需要从相关峰的索引中减去1。使用Matlab，我们可以找到正确的位偏移量“off”，如下所示：

off=find(cor==max(cor))−1.

9.创建误差向量

使用Matlab，我们从发送的位向量“tx”和接收的位向量“rx”计算误差向量“err”，偏移量为“off”，即：

err=tx-rx（off+1：length（tx）+off）

10.计算错误比特
使用Matlab，我们从误差向量“err”中计算出位错误总数“te”，即：

te=sum（abs（err））

11.计算误比特率

利用Matlab，我们计算了误比特率“ber”，即：

ber=te/length（tx）