first edit: 20170609
last edit: 20170904
(总结自《大话数据结构》,《算法 第四版》。代码胡写的,只保证实现功能。供自己回忆,部分细节需要看书)
(有错误,或代码可以改进的地方,求告知~~)
排序的相关概念
- 排序的稳定性
- 内排序
- 外排序
排序方法
- 冒泡、选择、插入、希尔、归并、堆、快速
排序方法的选择
- 总结陈述(待改):当待排序元素的关键字随机分布,同时不要求稳定排序的情况下,用快速排序。要求稳定,则用归并排序;当待排序序列基本有序时,使用简单插入排序;
- 时间复杂度上:快速、归并、堆 ,快速排序会出现最坏情况,而其余两种不会,当序列随机分布时,选择快排> 希尔排序 > 插入、选择、冒泡
- 空间复杂度上:堆排序最优,快排看情况最差的是顺序或者逆序O(n),归并最差(要构造辅助数组需要线性空间复杂度)
- 快排、堆排序不稳定,归并希尔插入选择冒泡排序稳定
- 常用快排而很少用堆排序是因为快排的局部访问性 locality of reference更好,而堆排序则需要大量的访问位置上不相邻的元素,导致缓存未命中次数增加。
复杂度总结
注意:
- 冒泡排序最好O(n),是在 大话数据结构p382 的改进代码的情况下。该改进只是能在输入序列尾部若干个元素有序的情况下降低比较次数。如不采取此改进,则冒泡排序复杂度为O(n平方)。
- 希尔排序复杂度与增量序列有关,此处使用的增量序列为h=3*h+1。但是按照《算法第四版》的说法,希尔排序即使在最坏情况下运行时间也达不到平方级别。最坏情况下复杂度为O(n^1.5),平均为O(nlogn)。
一、冒泡排序
- 思路
-
将较小的数字(如同气泡般)浮到顶端。
- 实现
void BubbleSort(int* data, int length) {
// data:指向整形数组的指针
// length:数组大小
int temp;
for (int i = 0; i < length; i++)
for (int j = length - 1; j > i; j--) {
if (data[j] < data[j - 1]) {
temp = data[j];
data[j] = data[j - 1];
data[j - 1] = temp;
}
}
}
- 复杂度分析
- 时间复杂度:需要比较 (n-1)+...+2+1 = n(n-1)/2次, 复杂度O(n^2)
- 空间复杂度:仅交换元素时需要一个额外的空间。O(1)
二、选择排序
- 思路
- 每次选择未排序数列中关键字最小的记录
- 实现
void SelectSort(vector &data) {
// data:待排序的vector
int length = data.size();
for (int i = 0; i < length; i++) {
int min = i;
for (int j = i + 1; j < length; j++) {
if (data[j] < data[min])
min = j;
}
swap(data,i,min);
}
}
- 复杂度
- 时间复杂度:需要比较 (n-1)+...+2+1 = n(n-1)/2次, 复杂度O(n平方)→?咋打上标,待改。
- 空间复杂度:仅交换元素时需要一个额外的空间。O(1)
三、插入排序
- 思路
- 类似理扑克,将一个记录插入到已经排序的序列中,得到长度+1的序列。插入方式为从后往前比较,直至找到合适位置
- 实现
void InsertSort(int *data, int length){
// 每次都将一个记录插入到已经排序的序列中
for (int i = 1; i < length; i++){
for (int j = i; j > 0 && (data[j] < data[j - 1]); j--){
int temp = data[j];
data[j] = data[j - 1];
data[j - 1] = temp;
}
}
}
- 复杂度
- 时间复杂度:最坏情况(输入逆序)下,需要1+2+...+(n-1)次,复杂度O(n平方)
- 空间复杂度:仅交换元素时需要一个额外的空间。O(1)
- 扩展
- 虽然插入排序和冒泡/选择排序最坏情况均为平方复杂度,但除非是逆序输入。插入排序所需比较次数均小于另外两者。
- 倒置:指数组中两个顺序颠倒的元素→部分有序数组,数组中倒置数目小于数组大小的某个倍数
- 对于部分有序的输入序列插入排序的性能较好
- 实际上,插入排序需要的交换操作和数组中倒置的数量相同(因为一次交换能减少一堆倒置),而比较次数则大于等于倒置次数(顺序输入),小于等于倒置数量加数组大小减一(逆序输入)
四、希尔排序
- 思路
- 将相距某个“增量”的元素组成一个子序列,在子序列中进行插入排序。然后按照某种规则逐渐减小增量至1(所谓增量序列)。这样就实现了整个数组的排序。
- 希尔排序的好处在于,一开始的子序列较小,倒置数量少,适用于插入排序。后面序列变长,但是由于前面的比较交换,此时序列倒置数量已经大大减小,同样能使用插入排序在较低的时间复杂度下完成排序。
- 增量序列影响算法的复杂度。这里使用h = 3*h + 1
- 实现
void ShellSort(int *data, int length){
// 先将序列分成小段,每小段插入排序
int h = 1;
while (h < length)
h = h * 3 + 1;
while (h >= 1){
for (int i = h; i < length; i++){
for (int j = i; j >= h && (data[j] < data[j - h]); j -= h){
int temp = data[j];
data[j] = data[j - h];
data[j - h] = temp;
}
}
h /= 3;
}
}
- 复杂度
- 时间复杂度:与增量序列有关,在h=3*h+1增量序列下,最坏情况下复杂度为O(n^1.5),平均为O(nlogn)。
- 空间复杂度:仅交换元素时需要额外的空间。O(1)
- 扩展
- 希尔排序是一种能够在空间复杂度较低的情况下,时间复杂度相对也较低的算法。如果待排序数组很大,或者系统内存有限时,可以考虑。
- 堆排序同样也是空间复杂度较低的前提下,时间复杂度相对较低。但是存在问题(见堆排序分析)
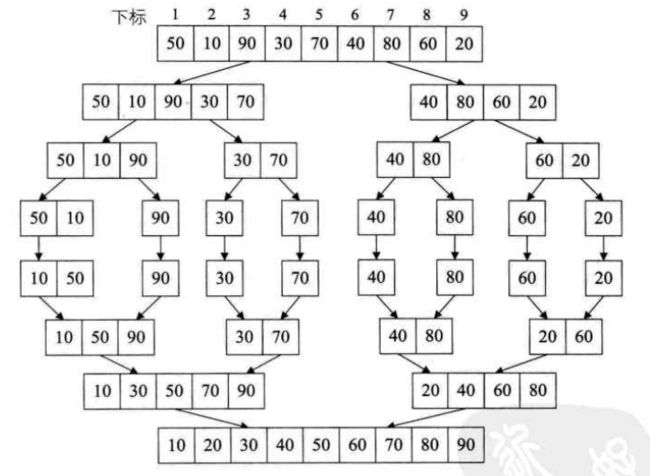
五、归并排序
- 思路
- 将数组划分为较小的数组,分别排序,然后归并两个有序数组。
-
分治的思想,使用了递归。
- 实现
void MSort(int *, int *, int, int);
void Merge(int *, int *, int, int, int);
void MergeSort(int*data, int length){
int *aux = new int[length];
MSort(data, aux, 0, length - 1);
delete[] aux;
}
void MSort(int *data, int *aux, int low, int high){
if (high <= low)
return;
int mid = (low + high) / 2;
MSort(data, aux, low, mid);
MSort(data, aux, mid + 1, high);
Merge(data, aux, low, mid, high);
}
void Merge(int *data, int *aux, int low, int mid,int high){
int index1 = low, index2 = mid + 1;
for (int k = low; k <= high; k++){
aux[k] = data[k];
}
for (int k = low; k <= high; k++){
if (index1 > mid)
data[k] = aux[index2++];
else if (index2 > high)
data[k] = aux[index1++];
else if (aux[index2] < aux[index1])
data[k] = aux[index2++];
else
data[k] = aux[index1++];
}
}
- 复杂度
- 时间复杂度:每次归并所需时间为O(n),需要O(logn)次归并,所以复杂度为O(nlogn);
- 空间复杂度:辅助数组,O(n);栈空间,O(logn)。
- 扩展
- 辅助数组不要在递归函数中建立,因为这样需要多次重新分配空间建立数组。
六、堆排序
- 思路
-
建立大顶堆,然后再依次取出最大元素放在数组尾部。
- 实现
void heapAdjust(int *data, int father, int end){
while (2*father<=end){
int son = 2 * father;
if (son < end && (data[son-1] < data[son]))
son++;
cout << data[son - 1] << endl;
cout << data[father -1] << endl;
if (data[son - 1] <= data[father - 1])
break;
swap(data, father-1, son-1);
father = son;
}
}
void HeapSort(int *data, int length) {
for (int i = length / 2; i >= 1; i--)
heapAdjust(data, i,length);
for (int i = length; i >0; i--){
swap(data, 0, i - 1);
heapAdjust(data, 1, i - 1);
}
}
- 复杂度
- 时间复杂度:在构建大顶堆时,每个非终端节点(书中说法,就是指还有子节点的节点),最多进行两次比较和互换。正式排序时,取堆顶记录需要用O(log n)的时间(这是因为堆的深度是对数级的),需要取n-1次记录。综合起来复杂度为O(nlogn)。
- 空间复杂度:仅交换元素时需要一个额外的空间。O(1)
- 扩展
- 优先队列是二叉堆的重要应用,《算法第四版 2.4节》;
- 堆是目前已知唯一能在时间复杂度为线性对数的情况下,保证空间复杂度较低的算法。但是在实际中应用较少,这是因为数组元素很少和相邻的其它元素进行比较,使得它无法利用缓存,缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法。
七、快速排序
- 思路
- 通过一趟Partition,将待排序数组分割成独立的两部分,其中一部分元素均比另一部分元素小。
-
例如下图,通过一次Partition,将50放在数组中合理的位置,其左侧元素均小于50,右侧均大于50。
- 实现
int Partition(vector&, int, int);
void QSort(vector&, int, int);
void QuickSort(vector &data) {
// data:待排序的vector
// length:数组大小
QSort(data, 0, data.size() - 1);
}
void QSort(vector &data, int low, int high) {
if (high <= low)
return;
int mid = Partition(data, low, high);
QSort(data, low, mid - 1);
QSort(data, mid + 1, high);
}
int Partition(vector &data, int low, int high) {
int index1 = low, index2 = high + 1; //从两端开始扫描
int flag = data[low]; //切分元素
while (true) {
while (data[++index1] < flag) //左侧扫描探针向中间移动
if (index1 == high)
break;
while (data[--index2] > flag) //右侧扫描探针向中间移动,--index2,所以初始值为High+1
if (index2 == low)
break;
if (index1 >= index2) //相遇时退出
break;
swap(data, index1, index2); //交换左边比flag大的元素和右边比flag小的元素
}
swap(data, low, index2);
return index2; //注意理解为啥返回的是Index2
}
- 复杂度
- 时间复杂度:若每次切分元素都选取为部分数组的首位。最好情况下,每次选取的恰为居中的元素,复杂度为O(nlogn)。最坏情况下,若输入为顺序或者逆序,需要平方级的复杂度。
- 空间复杂度,主要是递归造成栈空间的使用,空间复杂度为O(logn)。
- 扩展
- 切分元素的选择对,时间复杂度影响较大。
- 可以使用三数取中,或者先打乱输入数组顺序的方法来选择切分元素。