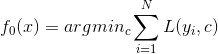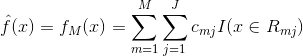传统机器学习-提升方法
在分类问题中,通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,以提高分类器的性能。
提升方法需要回答两个问题:
- 每一轮如何改变训练数据的权值或概率分布
- AdaBoost:提高那些被前一轮弱分类器错误分类样本的权值,降低被正确分类样本的权值
- 如何将弱分类器组合成一个强分类器。
- AdaBoost:加权多数表决,加大分类误差率小的弱分类器的权值,使其在表决中起较大作用,减小分类误差率大的弱分类器的权值
AdaBoost算法算法流程
训练数据集:![]() ,
,![]()
输出:最终分类器G(x)
(1)初始化训练数据的权值分布,初始具有均匀的权值分布,即每个训练样本在基本分类器的学习作用相同。
(2)对
(a)使用具有权值分布
的训练数据集学习,得到基本分类器
(b)计算
在训练数据集上的分类误差率,分类误差率是被
误分类样本的权值之和。
(c)计算
的系数,我们可以看出当
,
,并且
随着
的减小而增大。
(d)跟新训练数据集的权值分布
(3)
其中
是规范化因子,他使
成为一个概率分布
弱分类器只那些比随机猜测略好的分类器,即
,则有
,被基分类器
错误分类的样本的权值得以扩大,被正确分类样本的权值得以缩小。
(3)构建基本分类器的线性组合,
随着
的减小而增大,即分类误差率越小的基本分类器在最终分类器中的作用越大。
得到最终分类器,f(x)的符号决定实力x的类,f(x)的绝对值表示分类的确信度。
AdaBoost算法的解释
AdaBoost是模型为加法模型,损失函数为指数函数、学习算法为前向分步算法时的二分类算法。
前向分步算法
加法模型
给定训练数据及损失函数L(y,f(x))的条件下,学习加法模型f(x)成为经验风险极小化即损失函数极小化问题:
对该问题进行简化,前向分步算法的思路:从前向后,每次只学习一个基函数及其系数,逐渐逼近优化目标函数式(9),即每步只需优化:
输出:加法模型f(x)
(1)初始化
(2)对
(a)极小化损失函数,得到参数
(b)更新
(12)
(3)得到加法模型
前向分步算法与AdaBoost
AdaBoost算法是前向分步加法算法的特例。这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。
要证 前向分步算法学习的是加法模型,当基函数为基本分类器时,该加法模型等价于AdaBoost的最终分类器
已知:模型是加法模型,损失函数是指数函数,损失函数公式如下
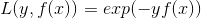
证明:假设经过m-1轮迭代前向分步算法已经得到
:
在第m轮迭代得到
,
和
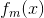
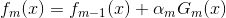
我们的目标是使前向算法得到的
,
使
在训练集T上的指数损失最小,即
式(15)可以表示为
其中
,因为
即不依赖于
也不依赖于
,所以与最小化无关,但是
依赖于
,随着每一轮迭代而发生变化。
首先求
,依据上下文,G输出的是类型,即非-1即+1,对
,
与最小化无关,固定
,则指数取值只能为
(当
时,即判断正确),或者
(当
时,即判断错误),这时取最小,只能是误判最小化
次分类器
即为AdaBoost算法的基本分类器G_m(x),因为它使第m轮迭代加权训练数据分类误差率最小的基本分类器。
再求
,式(16)中,
(17)
将已求得的
带入式(17),对
求导并使得导数为0,即得到使式(17)最小的
其中
是分类误差率
这里的
与AdaBoost算法2(c)步的
完全一致。
最后来看每一轮样本权值的更新,由
以及
,可得
这与AdaBoost算法第2(d)步的样本权值的更新,只相差规范化因子,因而等价。
提升树
提升树模型
可以表示为决策树的加法模型,其中![]() 表示决策树;
表示决策树;![]() 是决策树的参数;M是树的个数:
是决策树的参数;M是树的个数:
对分类问题决策树是二叉分类树;对回归问题决策树是二叉回归树。
提升树算法
初始提升树![]() ,第m步的模型是
,第m步的模型是
![]() (19)
(19)
其中,![]() 为当前模型,通过经验风险最小化确定下一棵决策树的参数
为当前模型,通过经验风险最小化确定下一棵决策树的参数![]()
针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。包括用平方误差损失函数的回归问题,用指数损失函数的分类问题,以及用一般损失函数的一半决策问题。
回归提升树
训练数据集
,
,若将输入空间
划分为
个互不相交的区域
,并且在每个区域上确定输出的常量
,则树可表示为:
其中,参数
表示树的区域划分和各区域上的常量,J是回归树的复杂度即叶节点的个数。
回归提升树使用一下前向分步算法:
在前向分步算法的第m步,给定当前模型
,需求解
得到
,即第m棵树的参数。
采用平方损失函数时,
其损失变为
这里,
(22)
是当前模型拟合数据的残差,所以对提升回归树算法来说,只需要简单的拟合当前模型的残差。
输出:提升树
(1)初始化
(2)对
(a)按式(22)计算残差
(b)拟合残差
学习一个回归树,得到
(c)更新
(3)得到回归提升树
梯度提升
梯度提升是针对一般损失函数的优化,利用最速下降法的近似方法,关键是利用损失函数的负梯度在当前模型的值
![]()
作为回归问题提升树算法中的残差近似值,拟合一个回归树。
输出:提升树
(1)初始化
(2)对
(a)按式(22)计算残差
(b)拟合残差
学习一个回归树,得到第m颗的叶节点区域
(c)对
,计算
(3)得到回归提升树
算法第1步初始化,估计使损失函数极小化的常数值,它是只有一个根结点的树,即 x>c 和 x
梯度提升树(GBDT)的基本结构是决策树构成的树林,学习的方式是梯度提升。形象理解如下:
具体来说,GBDT作为集成模型,预测的方式是把所有子树的结果加起来。
![]()
GBDT通过注意生成决策子树的方式生成整个树林,生成新子树的过程是利用样本标签值域当前树林预测值之间的残差,构建新子树。
假设当前已经产生了3颗子树,则当前的预测值为
![]()
GBDT期望的是构建第4颗子树,使当前树林的预测结果D(x)与第4颗子树的预测值![]() 之和,进一步逼近理论上的拟合函数f(x),即
之和,进一步逼近理论上的拟合函数f(x),即
![]()
则,第4颗子树生成的过程是一目标拟合函数和已有树林预测结果的残差R(x)为目标的:
![]()
参考 :统计学习方法,李航
深度学习推荐系统,王喆
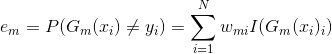

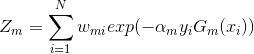
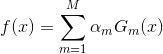

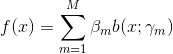
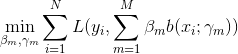
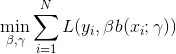
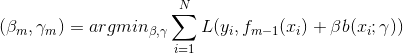
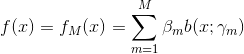
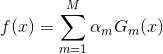
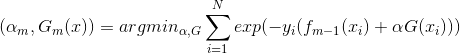
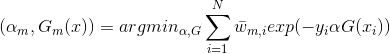



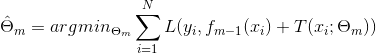


![\begin{aligned} &L(y_i,f_{m-1}(x_i)+T(x_i;\Theta_m)) \\ &=[y-f_{m-1}(x)-T(x;\Theta_m)]^2 \\ &=[r -T(x;\Theta_m)]^2 \end{aligned}](http://img.e-com-net.com/image/info8/896488c09d90429ab93d96911e2d83cf.gif)