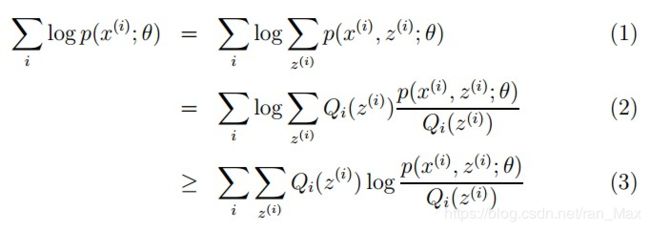对于EM算法的理解,看这一篇就够了
EM算法实际上就是含有隐变量的概率模型参数的极大似然估计法,或极大后验概率估计法。
其中对EM有两种理解,第一种是通俗的简单理解,另外一种对应的是李航的《统计学习方法》中的解释,其实两种理解都是一样的,只是角度不同,今天主要将一下通俗理解,改天有空再详细讲解一下《统计学习方法》的讲解(其实看懂了这一种那其实也差不多了)
文章目录
- 通俗理解
- 极大似然估计
- EM算法的思想
- EM算法的推导
- Jensen不等式
- EM算法的步骤
通俗理解
极大似然估计
假设现在有一个盒子,其中白球有99个,黑球有1个。那么我们很清楚的就可以得出我们从盒子里面摸一个球出来,摸到白球的概率是99/100,摸到黑球的概率是1/100。这就叫做先验概率。
现在假设盒子中有一种颜色的球有99个,另外一种颜色的球有1个,但是我们不知道是黑的是99个还是白的是99个。这时候我们从里面摸一个球出来,摸出来的是白色,那么这时候我们很自然的认为其中是白色的球有99个。有人会问:有没有可能其实是黑色的球是99个,白色的球是1个,恰好被我们摸出来了呢?显然是有可能的,但是这种可能性相较于前面一种就要小得多,我们更愿意“相信”其中是白色的球是99个。或者说白色球是99个的概率比黑色球是99个的概率要大。
现在假设盒子里面有黑色球和白色球共10000个,我们不知道其中的比例,我们采用放回摸取的方法摸了100次,其中白色被摸出了60次,黑色被摸出了40次,这种时候我们会很自然的认为其中白色球有6000个,黑色球有4000个。我们这种自然的认为就是似然估计。
似然估计实际上就是根据已经知道的结果去推测概率,这种的概率有很多种,其中包括黑色球1个,白色球99个;黑色球2个,白色球98个等等各种可能性,这样的每种假设都对应着一个概率,显然,我前面说的两种假设的概率都很低。所有可能的假设中,概率最大的一种假设,我们就把它近似的看成是实际情况,叫做极大似然估计。
我们给出公式如下,θ是参数,L(θ)表示参数取θ的概率,xi表示第i个球的颜色。p(xi;θ)表示在参数为θ时第i个球颜色为xi的概率。也就是我们给出一组样本,然后估计参数θ的值,我们每给出一个θ,L(θ)就对应有一个值,这个值代表的就是取这个θ的可能性。这个函数就叫做是似然函数,极大似然估计就是这个函数的最大值,当极大似然函数取最大的时候,这时的θ就是我们所求的结果,也就是最可能的结果。
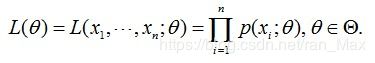
从公式我们可以看出,似然函数的值的求解实际上就是给定一个θ,我们就可以得到取出白球和黑球的概率,在这样的概率下,我们得到样本情况的概率的大小。
现在假设盒子里面不光有黑白两种颜色的球,而是有很多种颜色的球,这些球的颜色服从正太分布(也就是说每种颜色的球的概率可以用函数来表示,自变量是颜色,函数值是球为该种颜色的概率。但是该函数的参数我们不知道),我们依然是从中摸出10000个球,统计每种球的数量与比例。同样的,那么我们也可以根据样本的情况给出似然函数,用以来估计正太分布的参数。
具体的,我们一般解这个函数都是通过求导来完成的,为了方便计算,我们通常会对似然函数做对数处理,被叫做对数似然函数。
EM算法的思想
现在我们将情况复杂化,假设我们有2个盒子,盒子1号装有一定量(非常多)的各种颜色的球(各种颜色假设为无数种颜色),其中每种颜色的球的数量按照每种规律分布(假设服从正太分布,但是该分布的参数我们不知道);盒子2号与盒子1号一样,有各种颜色的球,也按照每种规律分布(也服从正太分布,但是正太分布的参数与盒子1号的参数不一定相同)。
对于盒子1号,我们从中抽出1000个球,按照前面的说法,我们可以通过这1000个球的颜色分布求出盒子1号的颜色分布的似然函数。对于盒子2号也是一样。
但是,假设我们现在2000个球,其中1000来自盒子1号,另外1000来自盒子2号,但是我们不知道每个球究竟是来自盒子1号还是盒子2号。用数学的语言说,抽取到的每个样本并不知道是从哪个分布得来的。那么,对于每一个球,我们要考虑两件事,第一件事就是这个球是来自盒子1号,还是盒子2号,第二就是两个盒子分布的参数是多少。只有当我们知道了这些球是来自1号还是2号的时候我们才能对于分布参数做出靠谱的推断。同样的,我们只有对两种概率做出了靠谱的推断后才能准确的判断出这个球更有可能来自1号还是2号盒子。这样就陷入了一种循环当中。为了打破僵局,我决定先随便给两个分布的参数赋一个值,根据这个参数我们可以得到盒子1号和来自盒子2号的分布,根据两个盒子的分布情况我们可以推断球更有可能来自哪个盒子,这样我们就可以把球分成来自盒子1号和来自盒子2号。我们知道了球来自哪个盒子之后,不就是前面说的问题了吗,我们就可以相对准确的求出分布的参数。得到一个更加准确的参数之后,又可以进一步计算盒子1号和来自盒子2号的分布。如此循环下去,越来越准确,直到收敛为止。
总的来说,EM的思想非常简单,我们要求AB两个参数,这两个参数都需要彼此才能求出,那么我们先人为给定A一个值,通过这个值可以算出B,然后我们通过算出的B再来求出A,这个时候的A比我们之前的A要更加准确,如此循环下去,我们就能得到较为准确的A和B。
为了各种读者更好的理解,我再通过上面的球的颜色问题举出一个例子,比如说我们对两个盒子的分布随机给定参数,这个时候我们就知道了每种颜色的球在每个盒子里面的概率。比如在盒子1号中,白球出现的概率是20%,在盒子2号中白球出现的概率是15%,现在有一个白色的球,我们就认为这个白球来自盒子1号。对于每一个球,我们都可以求出他到底是来自盒子1号还是盒子2号,也就是我们将每个球都分到了两个盒子中去,这就是步骤E。然后就回到了我们最开始所解释的,由于球属于哪个盒子已经确定了,我们对于每一个盒子都可以求出分布的参数,这就是步骤M。这个新的分布肯定比我们之前随机给定的要好,可以更进一步求出每种颜色的球到底属于1号盒子还是2号盒子。一直循环下去,直到基本不发生变化为止。
可能有人要问了,那我们能不能不管他们来自哪个盒子,把两个盒子看成是一个盒子,按照上面所说的求出来一个总体的似然函数不就行了吗,显然,这样是不够准确的,为什么不准确各位可以自己设计几个值亲自计算一下。
我们抽取出的样本,球的颜色是我们可以观测到的值,但是球来自哪一个盒子是我们不知道,那么球来自哪一个盒子可以视作为一个随机变量,这个随机是不可观测的。这个不可观测的隐含变量就是我们无法按照最开始简单的方法求解似然函数的原因。好,那么现在把这个复杂的问题逆回来,假设已经知道这个隐含变量了,求解那个分布的参数是不是很容易了(也就是上面说的步骤E),直接按上面说的最大似然估计就好了。这个隐含变量是未知的,你怎么就来一个假设说已知呢?你这种假设是没有根据的!那我们接着看:我们可以先给这个给分布弄一个初始值,然后求这个隐含变量的期望,当成是这个隐含变量的已知值,那么现在就可以用最大似然求解那个分布的参数了吧,那假设这个参数比之前的那个随机的参数要好,它更能表达真实的分布,那么我们再通过这个参数确定的分布去求这个隐含变量的期望,然后再最大化,得到另一个更优的参数,……迭代,就能得到一个皆大欢喜的结果了。
这种时候就又有人要问了,这种迭代你如何保证每一次的迭代都比上一次的好呢,又或者说你如何保证这个迭代是收敛的,不会无限进行下去呢??好吧,这些问题其实都是可以通过数学的推导解释的,我们只需要看懂这些推导能得出我们想要的结果就可以了,至于为什么要这样推导,那是数学家考虑的事情,如果你有兴趣的话,可以自己钻研一下
EM算法的推导
假设我们现在有一定的样本X={x(1),…,x(m)}。对于每一个样本有yi={xi,zi},xi代表球的颜色,zi待变球来自哪一个盒子(做出更一般化的假设,盒子也有很多个)。概率模型为p(xi,zi),p表示颜色为xi的概率。由于有zi这个隐含变量,我们很难用似然函数求出函数f的参数θ,如果知道zi这个变量,那么就好求解了。
下式左边表示的就是似然函数,我们要求出它的最大值。一个很自然的想法,我们对于θ和zi同时求导,另他们都等于0,那不就可以求出左边式子的最大值了吗。想法上是没错的,但是下面式子(1)我们可以看到有和的对数的形式,而且我们的样本往往是非常大的,这样的求导计算是不可行的,专业一点叫做没有解析解。所以我们按照下面的形式进行变形,从(2)到(3)的变换用到了Jensen不等式
Jensen不等式
对于Jensen不等式,不算特别难的概念,简单的说就是对于凸函数,自变量的期望的函数值<自变量函数值的期望,也就是E[f(X)]>=f(E[X])。对于凹函数,不等号反过来。各位可以先不管为什么,只需要知道这是个数学公式就好啦。
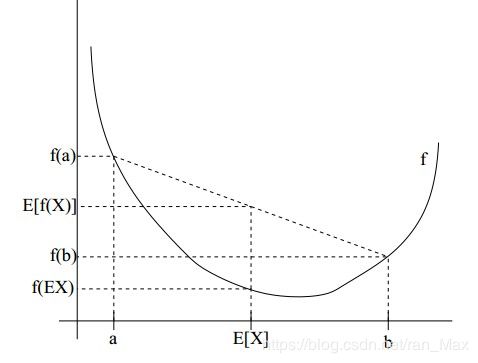
当我们求到(3)时,我们可以看到,已经没有和的对数了,转化成了对数的和,这样的求导计算就方便很多。
很多人就要问,这样的是一个不等式,我们求出的(3)式的最大值并不是左边式子的最大值啊。
接下来的步骤我认为就是理解EM的重点了。
左边式子的自变量为θ,我们将左边写作f(θ)。(3)式的自变量有两个,θ和Qi(zi),我们将右边写作h(θ,Q)。我们先任意给出一个θ0,此时θ固定,左边函数值就固定了,为f(θ0)。(3)式在固定θ的情况下,不断调整Q,有Q=Q1使(3)式与左边式子取等号(Jensen有具体的取等号条件),此时有,f(θ1)=h(θ1,Q1)。然后对于(3)式,再给定Q的情况下,我们再不断的调整θ,使(3)式达到当前最大值,此时为θ2。这时候,h(θ2,Q1)>h(θ1,Q1)=f(θ1),又因为f(θ2)>=h(θ2,Q1),所以f(θ2)>f(θ1),发现没有,我们这样改变θ的值会使得f的值增大了。我们可以认为,任何可以使h增大的θ值都会使f增大。

图画的不好,各位随便看一下,第一步:我们先在给定θ0情况下,调整Q让f和h(蓝色线)相等,然后我们取到h(蓝色线)的最大值,位于θ1点。第二步:然后我们固定θ1点,改变Q,使h(粉色线)和f在θ1点处相等(图形中自变量为θ,所以每次改变Q会使得图中h发生变化),然后我们取得粉色线的最大值,此时为θ2,我们可以明显看到f(θ2)>f(θ1)>f(θ0),也就是说我们每一次改变θ的取值都能够使得f的取值增大。如此下去,直到得到f(θ)的最大值。(实际情况,并不一定能得到f(θ)的最大值,只能得到局部最大值)
再大体情况搞清楚之后,我们来思考一个问题,什么时候h(θ,Q)和f(θ)取等号。Jensen不等式告诉我们,在X取得场常数的时候,具体到问题,就是下式成立的时候。

然后我们可以推导出,对于每一个i都有上式成立,又因为![]() 将分子分母对Z累加可得,
将分子分母对Z累加可得,![]() 的和就是c
的和就是c
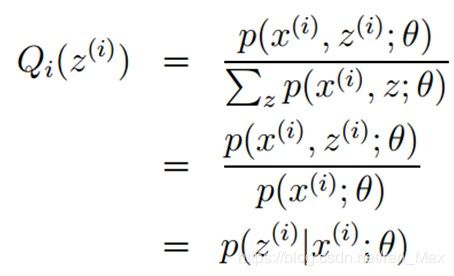
也就是Qi(Zi)=p(zi | xi ;θ)的时候取得等号。
EM算法的步骤
再回过头看,对于θi,我们求出Q(θi)的值
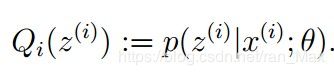
此时h和f相等。然后我们求解下式
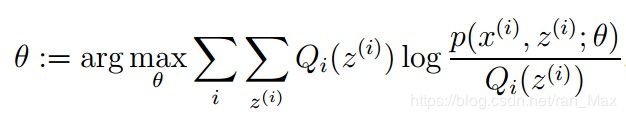
大多是通过求解,求出新的θi+1的值,新的θ能够使得f增大,然后再对新的θi+1,再求出新的Q(θi+1),再求出新的θi+2,依次类推,f每次都在增大,直到收敛
关于如何收敛,为什么一定会收敛,不做讲解
参考博文
从最大似然到EM算法浅解
浅谈EM算法的两个理解角度