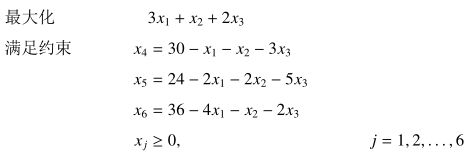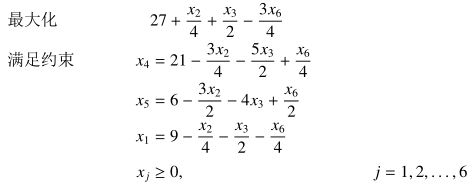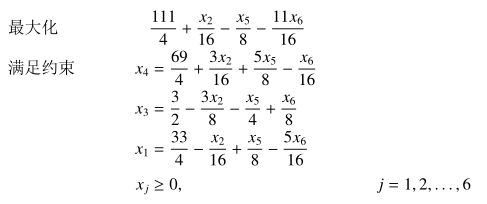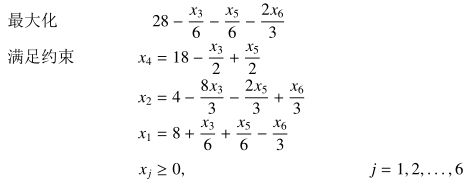单纯形法与线性规划

Preface

好久之前就想学学单纯形法了，因为据说用途非常广泛，而且最近恰好要做有关的题目

感觉还是挺高级的一个姿势吧，以下参考自一,二以及2016年的集训队论文,最后看的是bzt的板子，默认大家都知道线性规划是什么且具有一定线性代数的基础（好把没有也没有关系）

---

线性规划的标准型与松弛型

线性规划的标准型一般是这样的：

而松弛型是这样的：

桥豆麻袋，上面的标准型我能理解，这个松弛型是个什么鬼东西，怎么让变量更多了呢？

不要慌我们来观察一下，标准型简洁是简洁，但是它的约束符号是不等号（小于等于），而松弛型的约束符号是等号，众所周知等号比不等号要好处理的多

而它的转化也很简单，就是用一个松弛变量来表示不等式的差值，从而即保证了\(x_j\ge 0\)也化不等号为等号

同理这个操作对于大于等于号也适用，再网络流解线性规划也有用处，是非常常用的套路

然后我们像这样的等式$$x_{i+n}=b_i-\sum_{j=1}^n a_{i,j}x_j$$的左边的变量称为基变量，在松弛型里就是\(x_{n+1},x_{n+2},\cdots,x_{n+m}\)，把右边的那些变量称为非基变量，在松弛型里就是\(x_1,x_2,\cdots,x_n\)

---

单纯形法的核心思想

接下来我们以一个例子入手单纯形法的核心思想

然后我们来考虑一种情况，当所有\(b_i\)非负时，我们显然可以令所有非基变量都为\(0\)从而得到一组初始解即\(x1=x2=x3=0\)

但是这样的解显然不一定是最优的（显然不是最优的），因为最上面的式子的非基变量前的系数是正的，根据高中必修课本上都有的线性规划知识，我们知道这样一定不是最优解，因为我们可以通过变量的替代使得一些系数为正非基变量取到更大的值

桥豆麻袋，你刚才说了变量的替代？这是什么意思？

很简单，我们得到的松弛型规划式子的本质其实是方程组，而方程组之间不同的变量是可以互相代换的，换句话说我们最后答案的表达式中不一定一定要用原来的\(x_1,x_2,\cdots,x_n\)，等价地把\(x_{n+1},x_{n+2},\cdots,x_{n+m}\)换过去也是可以的

这就启发了我们如何判断一个解是否为最优解：最大化的式子右边所有非基变量之前的系数均非正时线性规划取得最优解

那么我们发现这个变量的替代操作很关键，它的核心就是把一个基变量\(x_{n+l}\)和\(x_e\)互换，即让原来的基变量成为非基变量，原来的非基变量称为基变量

先来考虑这个互化的问题，我们把这个操作叫做pivot（转轴），对于pivot(l,e)，从式子的角度考虑：

\[x_{n+l}=b_l-\sum_{j=1}^n a_{l,j}x_j=b_l-\sum_{j=1}^n [j\not = e] a_{l,j}x_j-a_{l,e}x_e \]

则有：

\[x_e=\frac{b_l-x_{n+l}-\sum_{j=1}^n [j\not =e] a_{l,j}x_j}{a_{l,e}} \]

然后再考虑其他的\(x_{n+i}(i\not=l)\)，把\(x_e\)用得到的式子全部代换掉就好了

知道了转轴操作之后我们还要知道和基变量里的那个变量转轴才会让答案变优

还是来看上面的例子，我们把系数是正的\(x_1\)进行代换，分别考虑三个限制：

\[x_4=30-x_1-x_2-3x_3\Leftrightarrow x_1\le 30 \]

\[x_5=24-2x_1-2x_2-5x_3\Leftrightarrow x_1\le \frac{24}{2}=12 \]

\[x_6=36-4x_1-x_2-2x_3\Leftrightarrow x_1\le \frac{36}{4}=9 \]

由于\(x_1\le 9\)的限制最紧，因此我们要用\(x_1\)去代换\(x_6\)，然后就可以得到下面新的线性规划：

woc现在目标函数的最大值已经被我们增大到\(27\)了，但是由于后面的非基变量的系数还是有正的，因此我们再给\(x_3\)做代换得到：

接下来还有\(x_2\)可以代换，得到：

此时由于所有非基变量的值都是负的，因此这就是线性规划的最优解

---

单纯形法的大致步骤

从上面的例子中我们大致对单纯形法的原理有了一定的了解，下面是它的伪代码（论文大法好）：

来我们可以大体描述一下这个simplex的过程（我看是complex还差不多）：

1. 在最终的最大化式子中找到一个满足\(c_e>0\)的非基变量\(x_e\)
2. 找到那个满足\(a_{l,e}>0\)且\(\frac{b_l}{a_{l,e}}\)最小的基变量\(x_{n+l}\)（结合前面所讲的，我们要找限制的最紧代换）
3. 执行pivot(l,e)，然后回到第一步

桥豆麻袋，万一死循环在这里了怎么办，那么意为着什么呢，必然有一个非基变量的系数在代换之后变成了\(0\)且其它的非基变量的系数都是负的

我们考虑它的几何意义，容易发现此时目标函数的梯度与某一个边界（即可行域的边界）正交了，因此说明目标函数的最优解有无限种（或者是无穷大）

那么我们就完成了单纯形法的主体部分了！

---

关于之前的一个假设

但是到这一步不知道大家是否记得，我们之前考虑的所有情况都在一个大前提下：\(b_i\)非负

而一旦\(b_i<0\)时，把所有的基变量代为\(0\)得到的非基变量不一定是一组合法解，那上面讲的东西就GG了

那么我们现在就需要一个初始化的操作，这个操作大致有两种实现，一种是论文里给出的构造辅助线性规划的方法，但是由于又要学习理论我比较懒，因此讲一种好写又好记的方法：

考虑我们的目标就是让所有\(b_i\)非负，那么我们找出\(b_i<0\)的基变量\(x_{n+i}\)，然后在它的右边找一个系数为正的非基变量，然后我们在对它们进行转轴操作

结合前面的式子我们发现若此时\(b_i\)仍为负那么显然是无解了，否则实现了化\(b_i\)为正的过程

---

关于单纯形法的复杂度

emmm……这个其实我也分析不来的说，只知道```pivot``的复杂度显然是\(O(nm)\)

由于一些奇奇怪怪的原因pivot的调用次数很少，因此一般在OI中能跑过几百的数据（怎么和它的好哥们网络流的复杂度有异曲同工之妙呢）

反正一般你能把一道题目化成单纯形法的时候直接干它就完了

---

模板

又到了喜闻乐见的放板子时间了，例题是UOJ上的版题UOJ #179. 线性规划，由于有毒瘤出题人卡精度卡时间等情况因此只要拿到97分就没什么问题了

#include
#include
#include
#include
#define RI register int
#define CI const int&
using namespace std;
const int N=25; 
const double EPS=1e-8;
int n,m,tp; double a[N][N];
namespace SM //Simplex Method
{
	int id[N<<1]; double ans[N];
	inline void pivot(CI l,CI e)
	{
		RI i,j; swap(id[n+l],id[e]); double t=a[l][e];
		for (a[l][e]=1,i=0;i<=n;++i) a[l][i]/=t;
		for (i=0;i<=m;++i) if (i!=l&&fabs(a[i][e])>EPS)
		for (t=a[i][e],a[i][e]=j=0;j<=n;++j) a[i][j]-=t*a[l][j];
	}
	inline bool init(void)
	{
		for (;;)
		{
			RI i; int l=0,e=0;
			for (i=1;i<=m;++i) if (a[i][0]<-EPS&&(!l||rand()&1)) l=i; if (!l) break;
			for (i=1;i<=n;++i) if (a[l][i]<-EPS&&(!e||rand()&1)) e=i;
			if (!e) return puts("Infeasible"),0; pivot(l,e);
		}
		return 1; 
	}
	inline bool simplex(void)
	{
		for (;;)
		{
			RI i; int l=0,e=0; double mi=1e9;
			for (i=1;i<=n;++i) if (a[0][i]>EPS) { e=i; break; } if (!e) break;
			for (i=1;i<=m;++i) if (a[i][e]>EPS&&a[i][0]/a[i][e]

---

例题

又到了喜闻乐见的放例题时间了：

• BZOJ 1061: [Noi2008]志愿者招募&&BZOJ 3265: 志愿者招募加强版

• BZOJ 3112: [Zjoi2013]防守战线

---

Postscript

线性规划真是可怕呢……