BP神经网络识别手写字体
摘自于《神经网络与深度学习》
mnist_loader.py
#coding:utf-8
import cPickle
import gzip
import numpy as np
def load_data():
f = gzip.open("F:/neuralnetwork/mnist.pkl.gz", "rb")
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
vadiation_inputs = [np.reshape(x, (784,1)) for x in va_d[0]]
validation_data = zip(vadiation_inputs, va_d[1])
test_inputs = [np.reshape(x,(784,1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
e = np.zeros((10, 1))
e[j] = 1.0
return e
neuralnetwork_sample1.py
#coding:utf-8
'''
神经网络识别手写字体
'''
import random
import numpy as np
def sigmoid(z):
return np.longfloat(1.0/(1.0+np.exp(-z)))
def sigmoid_prime(z):
return sigmoid(z)*(1-sigmoid(z))
class Network(object):
'''
神经网络
'''
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.bias = [np.random.randn(y,1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x,y in zip(sizes[:-1], sizes[1:])
]
def feedforward(self, a):
for b,w in zip(self.bias, self.weights):
a = sigmoid(np.dot(w,a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
if test_data:
n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)
]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0} : {1} / {2}".format(j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
nabla_b = [np.zeros(b.shape) for b in self.bias]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x,y in mini_batch:
delta_nabla_b,delta_nabla_w = self.backdrop(x, y)
nabla_b = [nb+dnb for nb,dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw,dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [
w - (eta/len(mini_batch))*nw
for w,nw in zip(self.weights, nabla_w)]
self.bias = [
b - (eta/len(mini_batch))*nb
for b,nb in zip(self.bias, nabla_b)
]
def backdrop(self, x, y):
nabla_b = [np.zeros(b.shape) for b in self.bias]
nabla_w = [np.zeros(w.shape) for w in self.weights]
activation = x
activations = [x]
zs = []
for b,w in zip(self.bias, self.weights):
z = np.dot(w, activation) + b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
delta = self.cost_derivative(activations[-1], y)*sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta)*sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
test_results = [(np.argmax(self.feedforward(x)),y) for (x,y) in test_data]
return sum(int(x==y) for (x,y) in test_results)
def cost_derivative(self, output_activations, y):
return (output_activations-y)
if __name__ == '__main__':
network = Network([2, 3, 1])
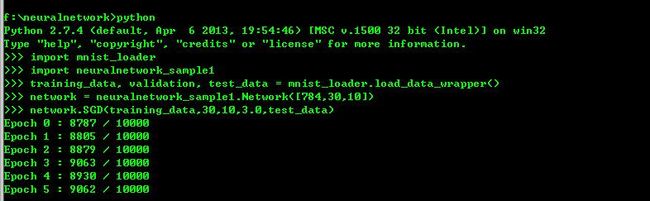
执行效果如下:
即10000个测试数据,识别准确的大概第五轮迭代时就超过90%的准确率了。
使用的数据集为MNIST手写字体数据集,下载地址为:mnist数据集