DFA的最小化
前面我们讲过NFA通过确定化能够得到DFA,现在我们看能不能让已经得到的DFA的状态数能不能再继续变小(minimise).其实也就是对优化再优化。
我们从NFA得到DFA的过程中有使用子集构造法。但是子集构造法的的状态数还是过多,达\(2^n\) 个。现在我们的目的就是进一步减少状态数。这样算法的复杂度才能减少。
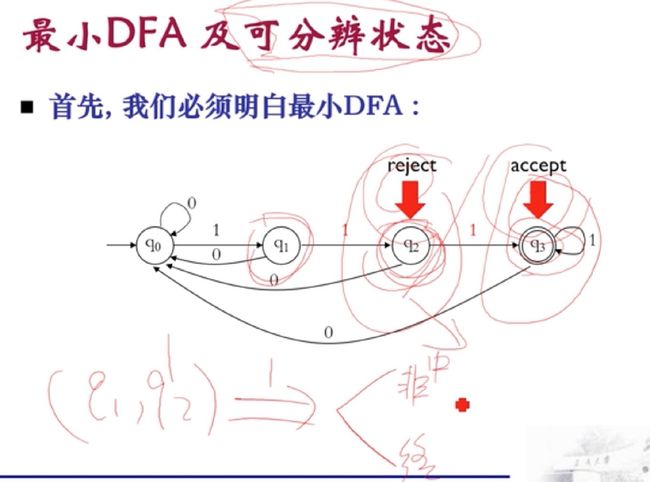
这个已经是最优化后的。现在我们问三个状态可不可以???
答案是不可以。最少4个。通过举例分析可以得到
DFA转化到最小DFA
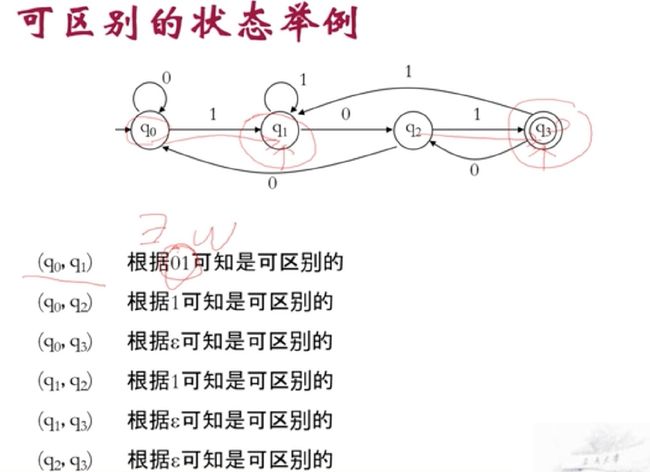
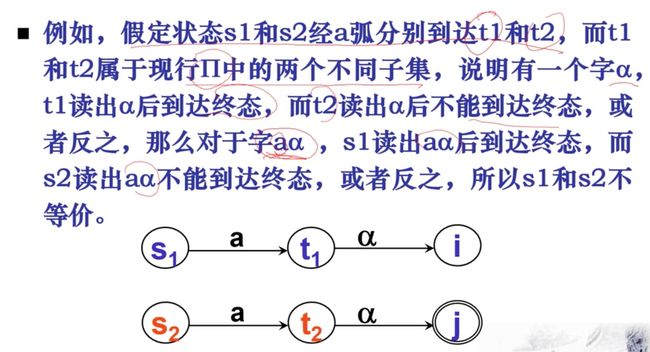
引入概念:可分辨状态——两个状态读入同一个串,到的两个不同的状态(比如一个拒绝状态,一个可分辨状态),这样就好可以区分开
最小的DFA = 每个状态都是可区分状态
\(C_4^2=6\) 6中比较完,就可以区别是可分辨的,既然全部可分辨,那么就是最小DFA
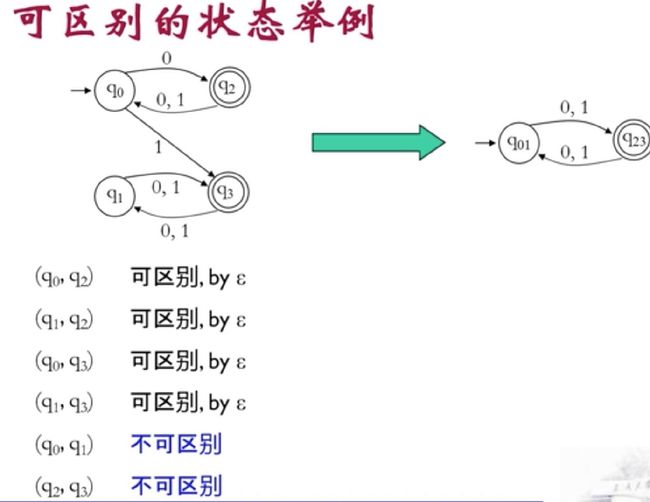
了解到 可区别状态和不可区别状态后,把不可区别状态对 合并之后就得到等价的最小DFA
这两个DFA仍然是等价的
不可区分状态的状态对是等价状态
核心是找不可区别状态,将不可区别的状态对合并即可
上面这个可以写成程序。规则1作为递归程序基础,规则2不断递归,规则3做最后扫底。
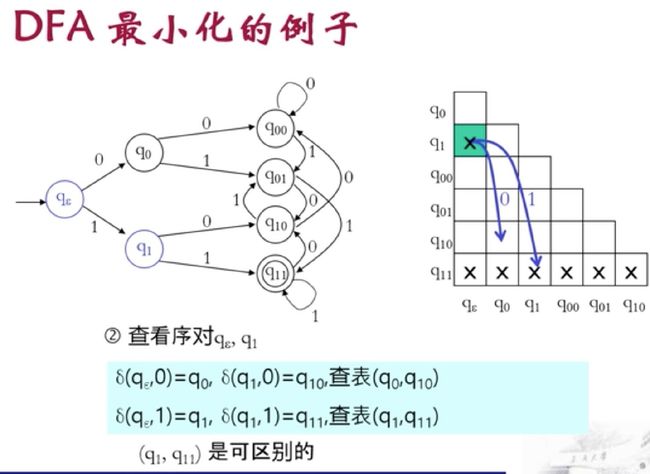
过程实例:方法叫做填表法
刚开始最底层第一行类似于我们规则1,是以后递归的基础
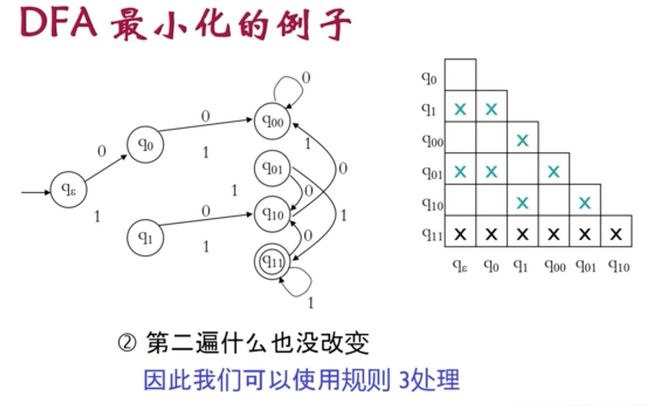
检查从左上角检查整张表一直到最底层
检查完第一遍再检查第二遍,如果发现检查完的结果和第一遍一样,那么就是用规则3扫底;如果发现第二遍发现有所收获、有所改变。那么再检查第三遍
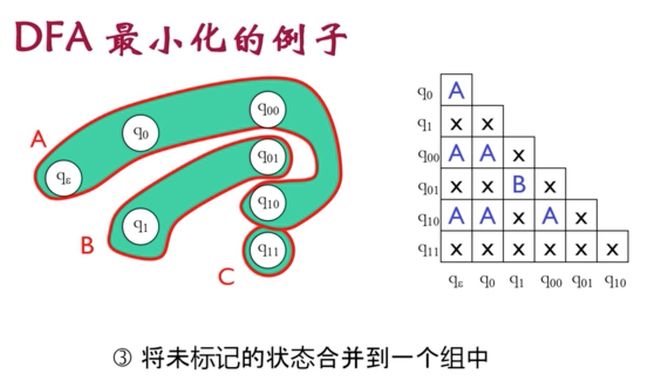
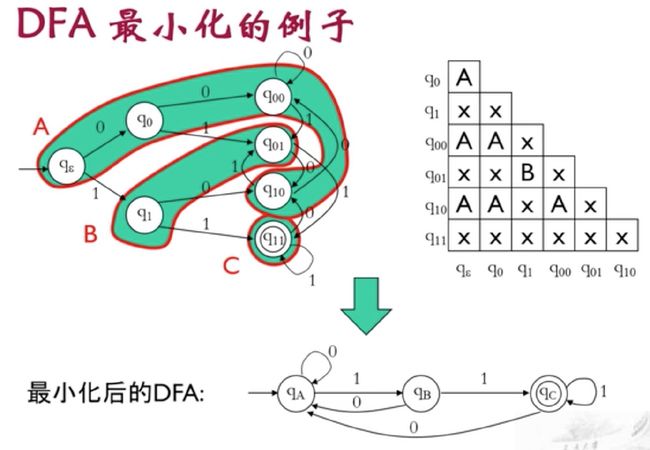
开始合并不可区分状态对的状态
画出最小化后的DFA
要是有题目给出疑似一个最小化,但我们仍然需要判定。就判断是否所有状态是可分辨的即可(反正状态已经最小化了,一般也不多\(C_n^2\)即可)
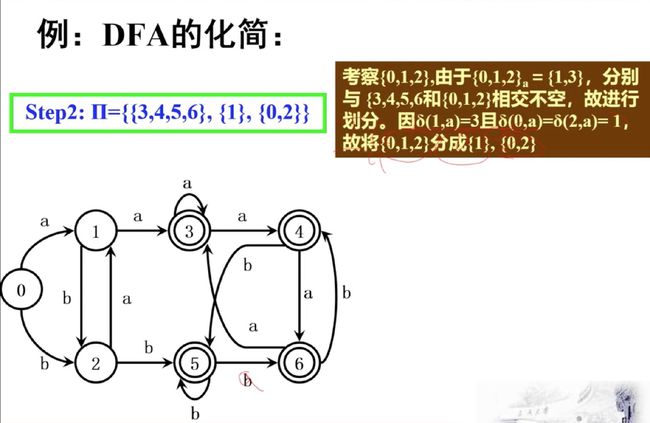
方法二 状态集划分法:由粗到精
具体步骤:
核心就是:对于初始化划分的状态集 加入字母表中的字符 ,看得到的状态集与原来状态集 的交集,如果交集不为空 把相交的部分单拎出来,成为一个独立的小团体。直至不再变化
遍历每个字母表的字母,用过的不再用
具体实例:
例题:
先划分初始状态 \(\{0,1\},\{2,3,4,5\}\) 这个比较好办,就是根据是否是接受状态划分即可。
然后对字母表中的a,b遍历进上面两个集合,直接对\(\{2,3,4,5\}\) 集合分析,{0,1}集合感觉属于贵宾席位算是第一梯队,我们的目的是在第二梯队的\(\{2,3,4,5\}\)再进行细分,得到第三梯队、第四梯队……。对于\(\{2,3,4,5\}\) a进入,得到\(\delta(2,a)=1,\delta(3,a)=3,\delta(4,a)=0,\delta(5,a)=5\) 首先知道的是,它们与原来的梯队有交集,可以肯定可以划分!!!然后再仔细看,发现虽然都"努力"了,但是这四个人的结果是不同的,\(\{2,4\}\)离第一梯队很近,\(\{3,5\}\)则距离较远。因此结果是\({\{0,1\},\{2,4\},\{3,5\}}\) .
然后继续用字母表里的字母分别对这3个集合做类似映射的操作。发现无论是a,b都不能有交集了,所以划分停止。
再对上面最后停止的操作,做扫尾工作。比较简单。可以得到最后的最小DFA。