BSGS_及其扩展算法

(Baby Step Giant Step)算法

BSGS存在的目的是求中x的解，

BSGS算法要求A与C互质，且C为质数

1. 令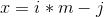，其中m=ceil(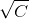),这样原式就变成了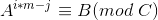，移项化简得到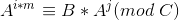
2. 先循环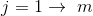（共有m项），将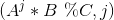存入Hash表中，这个就是Baby Steps
3. 再循环 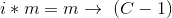 枚举左边多的部分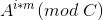，从hash表里面寻找是否有相同的，这就是（这就是Giant Step）
4. 找到相同的就是一组答案，

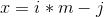
例题  poj2417  裸的BSGS算法

This is the code

#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define PI acos(-1.0)
#define EPS 1e-8
//#define MOD 1e9+7
#define LL long long
#define ULL unsigned long long     //1844674407370955161
#define INT_INF 0x7f7f7f7f      //2139062143
#define LL_INF 0x7f7f7f7f7f7f7f7f //9187201950435737471
const int dr[]={0, 0, -1, 1, -1, -1, 1, 1};
const int dc[]={-1, 1, 0, 0, -1, 1, -1, 1};
// ios.sync_with_stdio(false);
// 那么cin, 就不能跟C的scanf,sscanf,getchar,fgets之类的一起使用了。
#define mod 75643
struct Hash
{
    int ha;
    int id;
    int next;
}a[mod];
int head[mod];
int top;
void Insert(int x,int y)
{
    int k=x%mod;
    a[top].ha=x;
    a[top].id=y;
    a[top].next=head[k];
    head[k]=top++;
}
int Find(int x)
{
    int k=x%mod;
    for(int i=head[k];i!=-1;i=a[i].next)
        if(a[i].ha==x)
            return a[i].id;
    return -1;//表示没有找到
}
int BSGS(int a,int b,int c)
{
    if(b==1)
        return 0;
    memset(head,-1,sizeof(head));
    top=1;//一定要等于1
    int m=sqrt(c);
    LL p=1,x=1;
    for(int i=0;ic)
            break;
    }
    return -1;
}
int main()
{
    int a,b,c;
    while(scanf("%d%d%d",&c,&a,&b)!=EOF)
    {
        int ans=BSGS(a,b,c);
        if(ans==-1)
            printf("no solution\n");
        else
            printf("%d\n",ans);
    }
    return 0;
}

 扩展BSGS算法

扩展的BSGS不需要要求C为素数，大致的做法与原始的BSGS一致，只是有一条性质，

另

则有

等价于，之后再用BSGS算法计算就ok了

实际上问题变成了

注意：这种条件下，会导致（0-cnt）之间的解计算不出来，所以开始前要做一次之间的枚举（实际操作中验证（0-32）就行），直接验证是否成立

例题：poj3243 This is the link  裸的扩展BSGS算法

//BSGS的另一种计算方法

1. 令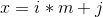，其中m=ceil(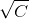),这样原式就变成了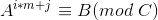，移项化简得到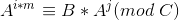
2. 先循环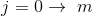（共有m项），将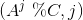存入Hash表中，这个就是Baby Steps
3. 再循环 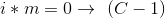 枚举左边多的部分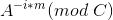，从hash表里面寻找是否有相同的，这就是（这就是Giant Step）
4. 找到相同的就是一组答案，
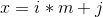
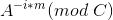5. 含有对除法的求模，需要用扩展欧几里得算法计算逆元得到结果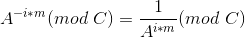,所以求其关于C的逆元

//这里使用了手写哈希表

This is the code

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include