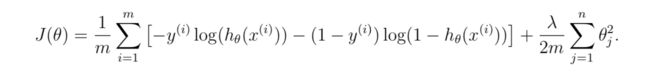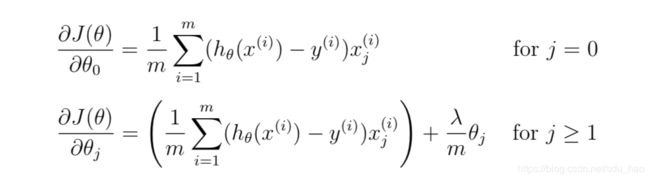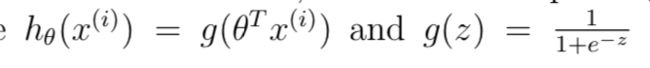机器学习 | 吴恩达机器学习第四周编程作业(Python版本)
实验指导书 下载密码:u8dl
本篇博客主要讲解,吴恩达机器学习第四周的编程作业,作业内容主要是对手写数字进行识别,是一个十分类问题,要求使用两种不同的方法实现:一是用之前讲过的逻辑回归实现手写数字识别,二是用本周讲的神经网络实现手写数字识别。实验的原始版本是用Matlab实现的,本篇博客主要用Python来实现。
目录
1.实验包含的文件
2.数据集
3.利用逻辑回归进行手写数字识别(多分类)
4.逻辑回归多分类器的完整项目代码
5.利用神经网络进行手写数字识别
6.神经网络分类器的完整项目代码
1.实验包含的文件
| 文件名称 | 含义 |
| ex3.py | 逻辑回归多分类器的主程序 |
| ex3_nn.py | 神经网络分类器的主程序 |
| ex3data1.mat | 手写数字数据集(.mat为Matlab矩阵格式) |
| ex3weights.mat | 神经网络的初始权重值(.mat为Matlab矩阵格式) |
| displayData.py | 可视化数据集 |
| sigmoid.py | Sigmoid函数 |
| lrCostFunction | 逻辑回归的代价函数(多分类) |
| oneVsAll.py | 训练逻辑回归多分类器 |
| predictOneVsAll.py | 用训练好的逻辑回归多分类器进行测试 |
| predict.py | 用神经网络模型进行预测 |
其中前六个文件已经写好了,实验任务是完成后四个文件的关键代码。
2.数据集
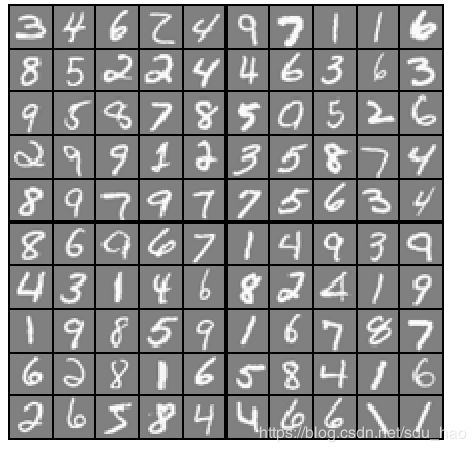
ex3data1.mat文件包含了5000个手写数字的训练样本,每个训练样本的输入是一张20*20的灰度图,输入特征是400维的,输出是一个标量,取值范围1-10,1-9依次代表数字1-9,10代表数字0.
3.利用逻辑回归进行手写数字识别(多分类)
- 打开逻辑回归多分类器的主程序ex3.py
- 加载需要的库
'''系统自带的库'''
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio #引入读取.mat文件的库
'''自己编写的库'''
import displayData as dd #引入可视化数据集的程序
import lrCostFunction as lCF #引入逻辑回归多分类代价函数
import oneVsAll as ova #引入逻辑回归训练程序
import predictOneVsAll as pova #引入逻辑回归预测程序- 首先加载数据集,并可视化前100个训练样本
input_layer_size = 400 # 输入特征的维度 每张数字图片20*20=400
num_labels = 10 # 10个标签 注意“0”对应第十个标签 1-9一次对应第1-9个标签
'''第一部分 加载手写数字训练数据集 并可视化部分训练样本'''
# 加载训练集
print('加载并可视化数据 ...')
data = scio.loadmat('ex3data1.mat') #读取训练集 包括两部分 输入特征和标签
X = data['X'] #提取输入特征 5000*400的矩阵 5000个训练样本 每个样本特征维度为400 一行代表一个训练样本
y = data['y'].flatten() #提取标签 data['y']是一个5000*1的2维数组 利用flatten()将其转换为有5000个元素的一维数组
m = y.size #训练样本的数量
# 随机抽取100个训练样本 进行可视化
rand_indices = np.random.permutation(range(m)) #获取0-4999 5000个无序随机索引
selected = X[rand_indices[0:100], :] #获取前100个随机索引对应的整条数据的输入特征
dd.display_data(selected) #调用可视化函数 进行可视化- 查看可视化程序displayData.py
def display_data(x):
(m, n) = x.shape #100*400
example_width = np.round(np.sqrt(n)).astype(int) #每个样本显示宽度 round()四舍五入到个位 并转换为int
example_height = (n / example_width).astype(int) #每个样本显示高度 并转换为int
#设置显示格式 100个样本 分10行 10列显示
display_rows = np.floor(np.sqrt(m)).astype(int)
display_cols = np.ceil(m / display_rows).astype(int)
# 待显示的每张图片之间的间隔
pad = 1
# 显示的布局矩阵 初始化值为-1
display_array = - np.ones((pad + display_rows * (example_height + pad),
pad + display_rows * (example_height + pad)))
# Copy each example into a patch on the display array
curr_ex = 0
for j in range(display_rows):
for i in range(display_cols):
if curr_ex > m:
break
# Copy the patch
# Get the max value of the patch
max_val = np.max(np.abs(x[curr_ex]))
display_array[pad + j * (example_height + pad) + np.arange(example_height),
pad + i * (example_width + pad) + np.arange(example_width)[:, np.newaxis]] = \
x[curr_ex].reshape((example_height, example_width)) / max_val
curr_ex += 1
if curr_ex > m:
break
# 显示图片
plt.figure()
plt.imshow(display_array, cmap='gray', extent=[-1, 1, -1, 1])
plt.axis('off')-
查看可视化效果
- 编写逻辑回归的代价函数(正则化)并做简单测试
注意使用矢量化编程。
'''第2-1部分 编写逻辑回归的代价函数(正则化),做简单的测试'''
# 逻辑回归(正则化)代价函数的测试用例
print('Testing lrCostFunction()')
theta_t = np.array([-2, -1, 1, 2]) #初始化假设函数的参数 假设有4个参数
X_t = np.c_[np.ones(5), np.arange(1, 16).reshape((3, 5)).T/10] #输入特征矩阵 5个训练样本 每个样本3个输入特征,前面添加一列特征=1
y_t = np.array([1, 0, 1, 0, 1]) #标签 做2分类
lmda_t = 3 #正则化惩罚性系数
cost, grad = lCF.lr_cost_function(theta_t, X_t, y_t, lmda_t) #传入代价函数
#返回当前的代价函数值和梯度值 与期望值比较 验证程序的正确性
np.set_printoptions(formatter={'float': '{: 0.6f}'.format})
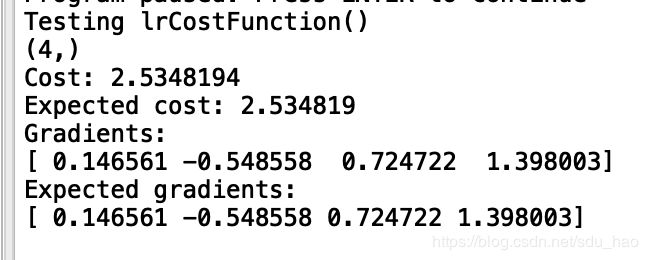
print('Cost: {:0.7f}'.format(cost))
print('Expected cost: 2.534819')
print('Gradients:\n{}'.format(grad))
print('Expected gradients:\n[ 0.146561 -0.548558 0.724722 1.398003]')带有正则化的逻辑回归代价函数表达式:
梯度计算:
其中:
在lrCostFunction.py中编写代码计算代价函数和梯度:
#sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))import numpy as np
from sigmoid import *
#逻辑回归的假设函数
def h(X,theta):
return sigmoid(np.dot(X,theta)) #X: m*(n+1) theta:(n+1,) 内积返回结果(m*1,)
#计算代价函数
def Compute_cost(theta, X, y, lmd):
m = y.size #样本数
cost = 0
myh=h(X,theta) #得到假设函数值
term1=-y.dot(np.log(myh)) #y:(m*1,) log(myh):(m*1,) 得到一个数值
term2=(1-y).dot(np.log(1-myh))#1-y:(m*1,) log(1-myh):(m*1,) 得到一个数值
term3=theta[1:].dot(theta[1:])*lmd #正则化项 注意不惩罚theta0 得到一个数值 thrta[1:] (n,)
cost=(1/m)*(term1-term2)+(1/(2*m))*term3
return cost
#计算梯度值
def Compute_grad(theta,X,y,lmd):
m = y.size #样本数
grad = np.zeros(theta.shape) #梯度是与参数同维的向量
myh=h(X,theta) #得到假设函数值
reg=(lmd/m)*theta[1:] #reg (n,)
beta=myh-y #beta: (m,)
grad=beta.dot(X)/m #beta:(m,) X:m*(n+1) grad:(n+1,)
grad[1:]+=reg
return grad
def lr_cost_function(theta, X, y, lmd):
cost=Compute_cost(theta, X, y, lmd)
grad=Compute_grad(theta, X, y, lmd)
return cost, grad
测试结果:
说明我们计算代价函数和梯度的代码正确。
- 训练逻辑回归多分类器
'''第2-2部分 训练多分类的逻辑回归 实现手写数字识别'''
print('Training One-vs-All Logistic Regression ...')
lmd = 0.1 #正则化惩罚项系数
all_theta = ova.one_vs_all(X, y, num_labels, lmd) #返回训练好的参数- 编写逻辑回归多分类器的训练程序one_vs_all.py
import scipy.optimize as opt #高级优化函数的包
import lrCostFunction as lCF
from sigmoid import *
#定义一个优化函数 实际上调用的是Python内置的高级优化函数
#可以把它想象成梯度下降法 但是不用手动设置学习率
''' fmin_cg优化函数 第一个参数是计算代价的函数 第二个参数是计算梯度的函数 参数x0传入初始化的theta值
args传入训练样本的输入特征矩阵X,对应的2分类新标签y,正则化惩罚项系数lmd
maxiter设置最大迭代优化次数
'''
def optimizeTheta(theta,X,y,lmd):
res=opt.fmin_cg(lCF.Compute_cost,fprime=lCF.Compute_grad,x0=theta,\
args=(X,y,lmd),maxiter=50,disp=False,full_output=True)
return res[0],res[1]
def one_vs_all(X, y, num_labels, lmd):
(m, n) = X.shape #m为训练样本数 n为原始输入特征数
'''
逻辑回归多分类器的训练过程:
用逻辑回归做多分类 相当于做多次2分类 每一次把其中一个类别当作正类 其余全是负类
手写数字识别是10分类 需要做十次2分类
比如:第一次把数字0当作正类 设置新的标签为1 数字1-9为负类 设置新的标签是0 进行2分类
第一次把数字1当作正类 设置新的标签为1 数字2-9和0为负类 设置新的标签是0 进行2分类
以此类推
'''
all_theta = np.zeros((num_labels, n + 1)) #存放十次2分类的 最优化参数
initial_theta=np.zeros(n+1) #每一次2分类的初始化参数值
X = np.c_[np.ones(m), X] #添加一列特征 值为1
for i in range(num_labels):
print('Optimizing for handwritten number {}...'.format(i))
iclass=i if i else 10 #数字0 属于第十个类别
logic_Y=np.array([1 if x==iclass else 0 for x in y]) #设置每次2分类的新标签
itheta,imincost=optimizeTheta(initial_theta,X,logic_Y,lmd)
all_theta[i,:]=itheta
print('Done')
return all_theta #返回十次2分类的 最优化参数
- 在训练集上测试分类器的准确率
'''第3部分 在训练集上测试 之前训练的逻辑回归多分类器的准确率'''
pred = pova.predict_one_vs_all(all_theta, X) #分类器的预测类别
print('Training set accuracy: {}'.format(np.mean(pred == y)*100)) #与真实类别进行比较 得到准确率- 编写测试程序predictOneVsAll.py
def predict_one_vs_all(all_theta, X):
m = X.shape[0] #shape[0]返回2维数组的行数 样本数
p = np.zeros(m) #存储分类器预测的类别标签
X = np.c_[np.ones(m), X] #增加一列1 X:5000*401
Y=lCF.h(X,all_theta.T) #all_theta:10*401 Y:5000*10 每一行是每一个样本属于10个类别的概率
p=np.argmax(Y,axis=1) #找出每一行最大概率所在的位置
p[p==0]=10 #如果是数字0的话 他属于的类别应该是10
return p- 分类器在训练集上的准确率
4.逻辑回归多分类器的完整项目代码
下载链接 下载密码:n3xy
5.利用神经网络进行手写数字识别
- 打开神经网络分类器的主程序ex3nn.py
- 引入必要的包
#系统自带包
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio #读取.mat文件
#手写的包
import displayData as dd #可视化数据
import predict as pd #神经网络分类器的预测程序- 加载数据集并可视化
input_layer_size = 400 # 输入层的单元数 原始输入特征数 20*20=400
hidden_layer_size = 25 # 隐藏层 25个神经元
num_labels = 10 # 10个标签 数字0对应类别10 数字1-9对应类别1-9
'''第1部分 加载数据集并可视化'''
print('Loading and Visualizing Data ...')
data = scio.loadmat('ex3data1.mat') #读取数据
X = data['X'] #获取输入特征矩阵 5000*400
y = data['y'].flatten() #获取5000个样本的标签 用flatten()函数 将5000*1的2维数组 转换成包含5000个元素的一维数组
m = y.size #样本数 5000
# 随机选100个样本 可视化
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[0:100], :]
dd.display_data(selected)- 查看可视化程序displayData.py
def display_data(x):
(m, n) = x.shape #100*400
example_width = np.round(np.sqrt(n)).astype(int) #每个样本显示宽度 round()四舍五入到个位 并转换为int
example_height = (n / example_width).astype(int) #每个样本显示高度 并转换为int
#设置显示格式 100个样本 分10行 10列显示
display_rows = np.floor(np.sqrt(m)).astype(int)
display_cols = np.ceil(m / display_rows).astype(int)
# 待显示的每张图片之间的间隔
pad = 1
# 显示的布局矩阵 初始化值为-1
display_array = - np.ones((pad + display_rows * (example_height + pad),
pad + display_rows * (example_height + pad)))
# Copy each example into a patch on the display array
curr_ex = 0
for j in range(display_rows):
for i in range(display_cols):
if curr_ex > m:
break
# Copy the patch
# Get the max value of the patch
max_val = np.max(np.abs(x[curr_ex]))
display_array[pad + j * (example_height + pad) + np.arange(example_height),
pad + i * (example_width + pad) + np.arange(example_width)[:, np.newaxis]] = \
x[curr_ex].reshape((example_height, example_width)) / max_val
curr_ex += 1
if curr_ex > m:
break
# 显示图片
plt.figure()
plt.imshow(display_array, cmap='gray', extent=[-1, 1, -1, 1])
plt.axis('off')
- 可视化效果
- 加载训练好的神经网络参数
因为本周的课程只讲了神经网络的前向传播,下周讲解神经网络的反向传播算法,来训练得到一组最优的参数。所以提供了训练好的参数,该实验只需要完成神经网络前向传播的预测过程,不涉及训练过程。
'''第2部分 加载训练好的神经网络参数'''
print('Loading Saved Neural Network Parameters ...')
data = scio.loadmat('ex3weights.mat') #读取参数数据
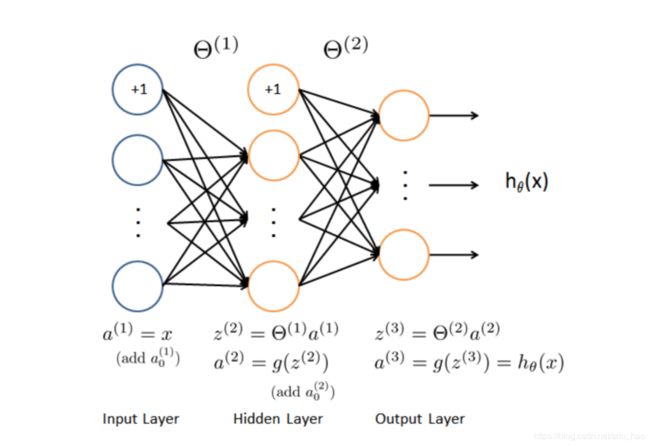
#本实验神经网络结构只有3层 输入层,隐藏层 输出层
theta1 = data['Theta1'] #输入层和隐藏层之间的参数矩阵
theta2 = data['Theta2'] #隐藏层和输出层之间的参数矩阵- 实现预测过程
'''第3部分 利用训练好的参数 完成神经网络的前向传播 实现预测过程'''
pred = pd.predict(theta1, theta2, X)
print('Training set accuracy: {}'.format(np.mean(pred == y)*100))- 编写神经网络的前向传播程序 predict.py
import numpy as np
from sigmoid import *
def predict(theta1, theta2, x):
#theta1:25*401 输入层多一个偏置项
#theta2:10*26 隐藏层多一个偏置项
m = x.shape[0] #样本数
num_labels = theta2.shape[0] #类别数
x=np.c_[np.ones(m),x] #增加一列1 x:5000*401
p = np.zeros(m)
z1=x.dot(theta1.T) #z1:5000*25
a1=sigmoid(z1) #a1:5000*25
a1=np.c_[np.ones(m),a1] #增加一列1 a1:5000*26
z2=a1.dot(theta2.T) #z2:5000*10
a2=sigmoid(z2) #a2:5000*10
p=np.argmax(a2,axis=1) #输出层的10个单元 第一个对应数字1...第十个对应数字0
p+=1 #最大位置+1 即为预测的标签
return p
- 在训练集上的预测准确率
6.神经网络分类器的完整项目代码
下载链接