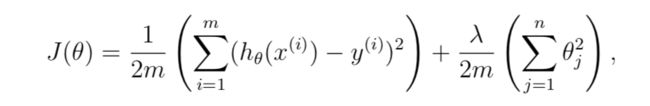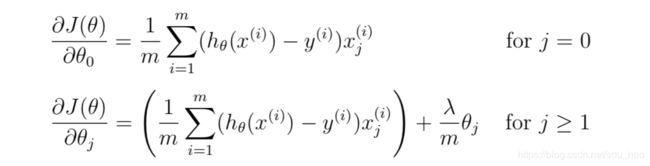机器学习 | 吴恩达机器学习第六周编程作业(Python版）

实验指导书    下载密码:ovyt

本篇博客主要讲解，吴恩达机器学习第六周的编程作业，作业内容主要是实现一个正则化的线性回归算法，涉及本周讲的模型选择问题，绘制学习曲线判断高偏差/高方差问题。原始实验使用Matlab实现，本篇博客提供Python版本。

目录

1.实验包含的文件

2.正则化线性回归算法

3.完整项目代码

---

1.实验包含的文件

文件名称	含义
ex5.py	实验主程序
ex5data1.mat	实验数据集
featureNormalize.py	特征缩放程序
learningCurve.py	绘制学习曲线程序
plotFit.py	绘制拟合曲线
linearRegCostFunction.py	线性回归(正则化）代价函数
trainLinearReg.py	训练程序
ployFeatures.py	为原始特征增加多项式特征
validationCurve.py	验证曲线

实验任务：完成红色部分程序的关键代码

 

2.正则化线性回归算法

• 打开主程序ex5.py

'''第1部分 加载并可视化数据集'''

print('Loading and Visualizing data ...')


data = scio.loadmat('ex5data1.mat')  #读取矩阵格式的数据集
#数据集已经被分成了训练集、验证集、测试集三部分
X = data['X']    #提取训练集原始输入特征   
y = data['y'].flatten()  #提取训练集输出变量 并转换成一维数组
Xval = data['Xval']   #提取验证集原始输入特征 
yval = data['yval'].flatten()#提取验证集输出变量 并转换成一维数组
Xtest = data['Xtest']#提取测试集原始输入特征   
ytest = data['ytest'].flatten()#提取测试集输出变量 并转换成一维数组

m = y.size #训练样本数

# 可视化训练集
plt.figure()
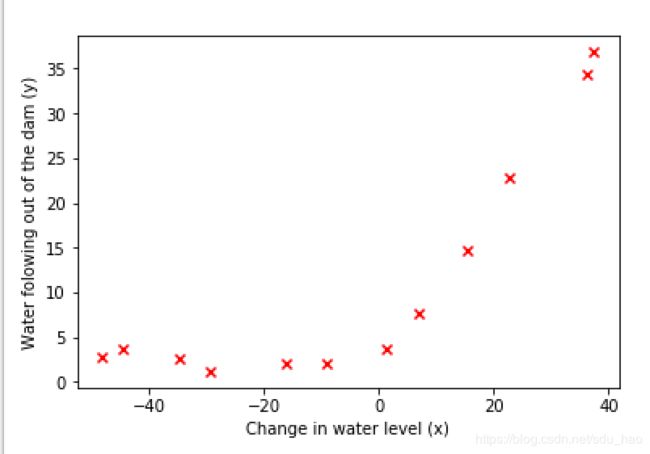
plt.scatter(X, y, c='r', marker="x")
plt.xlabel('Change in water level (x)')
plt.ylabel('Water folowing out of the dam (y)')

input('Program paused. Press ENTER to continue')

• 训练集可视化效果

• 计算正则化线性回归算法的代价函数

'''第2-1部分 编写正则化线性回归的代价函数'''

theta = np.ones(2)  #初始化参数为1  只有一个原始输入特征 所以两个参数
cost, _ = lrcf.linear_reg_cost_function(theta, np.c_[np.ones(m), X], y, 1) #为原始输入特征矩阵前面加一列1 正则化系数为1

#返回计算的代价并与期望进行比较 验证程序正确性
print('Cost at theta = [1  1]: {:0.6f}\n(this value should be about 303.993192'.format(cost))

input('Program paused. Press ENTER to continue')


'''第2-2部分 计算正则化线性回归的梯度'''


theta = np.ones(2)#初始化参数为1  只有一个原始输入特征 所以两个参数
cost, grad = lrcf.linear_reg_cost_function(theta, np.c_[np.ones(m), X], y, 1) #为原始输入特征矩阵前面加一列1 正则化系数为1

#返回计算的代价和梯度，并将梯度与期望进行比较  验证程序正确性
print('Gradient at theta = [1  1]: {}\n(this value should be about [-15.303016  598.250744]'.format(grad))

• 编写linearRegCostFunction.py

def h(theta,x):  #假设函数
    return x.dot(theta)

def linear_reg_cost_function(theta, x, y, lmd):
    
    m = y.size #训练样本数

   
    cost = 0
    grad = np.zeros(theta.shape)

    myh=h(theta,x) #假设函数值
    cost=(myh-y).dot(myh-h)/(2*m)+theta[1:].dot(theta[1:])*(lmd/(2*m)) #注意不惩罚第一个参数
    
    grad=（myh-h).dot(x)/m
    grad[1:]+=(lmd/m)*theta[1:]

    return cost, grad

与期望值一样，我们的程序是正确的：

• 训练线性回归

'''第3部分 训练线性回归'''
lmd = 0  #相当于不使用正则化

theta = tlr.train_linear_reg(np.c_[np.ones(m), X], y, lmd)  #返回训练后的最优参数

#画出拟合的曲线
plt.plot(X, np.dot(np.c_[np.ones(m), X], theta))

• 查看训练程序trainLinearReg.py

def train_linear_reg(x, y, lmd):
    initial_theta = np.ones(x.shape[1]) #初始化参数为1

    def cost_func(t): #计算代价
        return lrcf.linear_reg_cost_function(t, x, y, lmd)[0]

    def grad_func(t): #计算梯度
        return lrcf.linear_reg_cost_function(t, x, y, lmd)[1]

    #调用高级优化方法
    theta, *unused = opt.fmin_cg(cost_func, initial_theta, grad_func, maxiter=200, disp=False,
                                     full_output=True)
    #返回最优的参数
    return theta

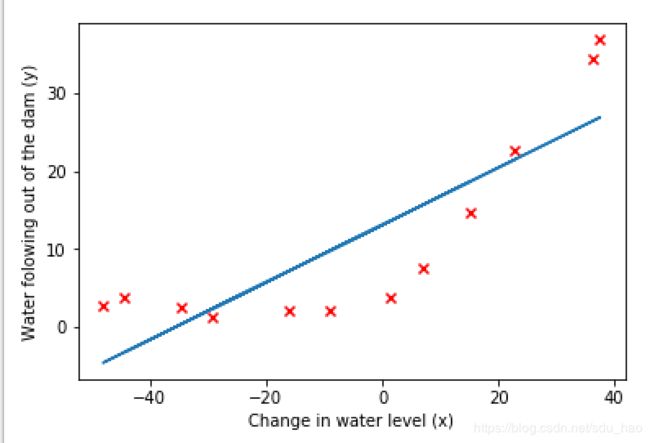
• 在训练集上的拟合效果

由于原始输入特征只有1个，所以模型的拟合效果不是很好，之后我们在原始输入特征的基础上增加多项式特征。

• 绘制此时的学习曲线

'''第4部分 绘制线性回归学习曲线'''
lmd = 0 #相当于不使用正则化
#返回不同训练样本下的训练误差和验证误差
error_train, error_val = lc.learning_curve(np.c_[np.ones(m), X], y, np.c_[np.ones(Xval.shape[0]), Xval], yval, lmd)

#绘制学习曲线
plt.figure()
plt.plot(np.arange(m), error_train, np.arange(m), error_val)
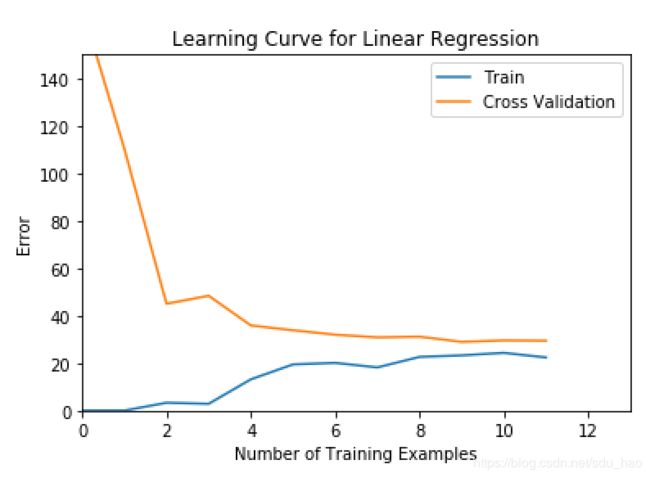
plt.title('Learning Curve for Linear Regression')
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('Number of Training Examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 150])

• 编写learningCurve.py

def learning_curve(X, y, Xval, yval, lmd):
    
    m = X.shape[0] #训练样本数

    error_train = np.zeros(m)  #不同训练样本对应的训练误差
    error_val = np.zeros(m)#不同训练样本对应的验证误差

    for i in range(m):
        x=X[:i+1,:]
        y1=y[:i+1]
        theta=tlr.train_linear_reg(x, y1, lmd)
        error_train[i]=lrcf.linear_reg_cost_function(theta, x, y1, lmd)[0]
        error_val[i]=lrcf.linear_reg_cost_function(theta, Xval, yval, lmd)[0]
    return error_train, error_val

• 可视化学习曲线

曲线特点：验证误差随样本增加不断减小，并趋于平缓；训练误差随样本增加不断增大，最后也趋于平缓；并且二者非常接近，交界处对应的误差比较大。

根据学习曲线的特点，此时模型出现了高偏差的情况，也就是欠拟合。此时增加更多的训练样本用处不大，应该增加更多的输入特征。

• 增加多项式特征

'''第5部分 增加多项式特征'''

p = 5 #多项式的最高次数 

#分别对训练集、验证集、测试集的原始输入特征矩阵增加新的多项式特征，返回新的输入特征矩阵 再加一列特征1 方便矩阵运算
#并对新的输入特征矩阵进行特征缩放 使各个特征的取值范围相近 加快优化速度
#验证集和测试集特征缩放使用的均值和方差 使用训练集计算的均值和方差

X_poly = pf.poly_features(X, p)
X_poly, mu, sigma = fn.feature_normalize(X_poly) 
X_poly = np.c_[np.ones(m), X_poly]


X_poly_test = pf.poly_features(Xtest, p)
X_poly_test -= mu
X_poly_test /= sigma
X_poly_test = np.c_[np.ones(X_poly_test.shape[0]), X_poly_test]


X_poly_val = pf.poly_features(Xval, p)
X_poly_val -= mu
X_poly_val /= sigma
X_poly_val = np.c_[np.ones(X_poly_val.shape[0]), X_poly_val]

print('Normalized Training Example 1 : \n{}'.format(X_poly[0]))

• 编写特征映射程序ployFeatures.py

def poly_features(X, p):
   
    X_poly=X[:]#第一列为原始输入特征
     #第2到p列 是原始输入特征的平方到p次方
    for i in range(2,p+1):
        X_poly=np.c_[X_poly,X**i]

    return X_poly

• 查看特征缩放程序featureNormalize.py

def feature_normalize(X):
    mu = np.mean(X, 0)  #求特征矩阵每一列的均值
    sigma = np.std(X, 0, ddof=1)#求特征矩阵每一列的标准差
    X_norm = (X - mu) / sigma  #对特征矩阵每一列进行缩放

    return X_norm, mu, sigma

• 增加特征后进行训练，可视化拟合效果和学习曲线

'''第6部分 增加多项式特征后进行训练  可视化拟合效果和学习曲线'''


lmd = 0 #不进行正则化
theta = tlr.train_linear_reg(X_poly, y, lmd) #训练得到最优参数

# 可视化训练集和拟合曲线
plt.figure()
plt.scatter(X, y, c='r', marker="x")
plotft.plot_fit(np.min(X), np.max(X), mu, sigma, theta, p)
plt.xlabel('Change in water level (x)')
plt.ylabel('Water folowing out of the dam (y)')
plt.ylim([0, 60])
plt.title('Polynomial Regression Fit (lambda = {})'.format(lmd))

#绘制学习曲线
error_train, error_val = lc.learning_curve(X_poly, y, X_poly_val, yval, lmd)
plt.figure()
plt.plot(np.arange(m), error_train, np.arange(m), error_val)
plt.title('Polynomial Regression Learning Curve (lambda = {})'.format(lmd))
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('Number of Training Examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 150])

print('Polynomial Regression (lambda = {})'.format(lmd))
print('# Training Examples\tTrain Error\t\tCross Validation Error')
for i in range(m):
    print('  \t{}\t\t{}\t{}'.format(i, error_train[i], error_val[i]))

• 拟合效果

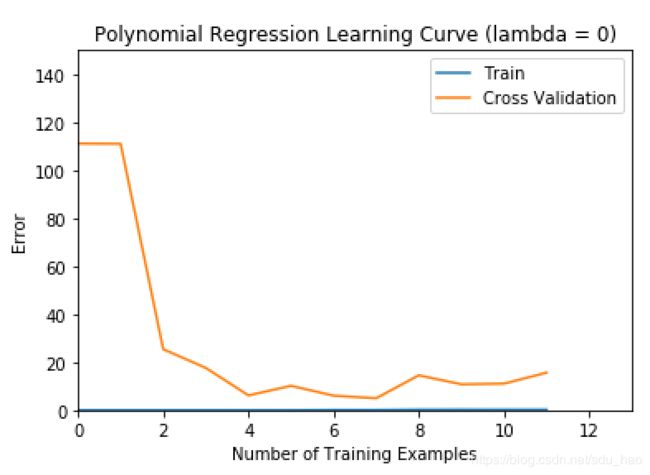
• 学习曲线

可以在增加多项式特征后，验证误差随训练样本的增加先不断减小，到达一个最优值后，又开始上升；而训练误差一直都非常小，几乎为0.可以判断此时出现了过拟合的情况，可以进行正则化，调整一下lambda的值。

• 模型选择，通过验证集选择一个最优的lambda值

'''第7部分 通过验证集选择一个最优的lambda值，模型选择'''

lambda_vec, error_train, error_val = vc.validation_curve(X_poly, y, X_poly_val, yval)

plt.figure()
plt.plot(lambda_vec, error_train, lambda_vec, error_val)
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('lambda')
plt.ylabel('Error')
print('验证误差')
print(error_val)
print('使验证误差最小的lambda取值:')
print(lambda_vec[np.argmin(error_val)])  #使验证误差最小的lambda取值

• 编写validationCurve.py

def validation_curve(X, y, Xval, yval):
    # 尝试不同的lambda值
    lambda_vec = np.array([0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10])

    # 每设置一个lambda值，进行训练，返回此时的训练误差和验证误差
    error_train = np.zeros(lambda_vec.size)
    error_val = np.zeros(lambda_vec.size)

    i=0
    for lmd in lambda_vec:
        print(lmd)
        theta=tlr.train_linear_reg(X, y, lmd)
        error_train[i]=lrcf.linear_reg_cost_function(theta, X, y,0)[0]#注意计算误差时lmd=0
        error_val[i]=lrcf.linear_reg_cost_function(theta, Xval, yval,0)[0]#注意计算误差时lmd=0
        i+=1
    print(error_train)
    return lambda_vec, error_train, error_val

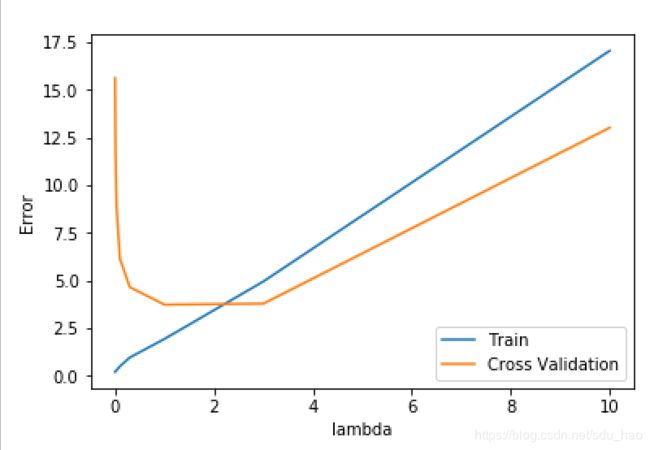
• 可视化不同lambda取值情况下，训练误差和验证误差曲线

所以正则化惩罚系数lambda的最佳选择时1.0。

3.完整项目代码

完整项目 提取码：hbbq