【opencv学习笔记】027之直方图反向投影 - calcBackProject函数详解

一、前言

        在学习直方图反向投影之前，如果你对直方图的概念，直方图均衡化，直方图计算等直方图相关的概念比较模糊，建议先了解一下

        1.直方图概念及直方图均衡化 https://blog.csdn.net/shuiyixin/article/details/80001756

        2.直方图计算 https://blog.csdn.net/shuiyixin/article/details/80032167

        3.直方图比较 https://blog.csdn.net/shuiyixin/article/details/80257822

如果你想了解更多有关于计算机视觉、OpenCV、机器学习、深度学习等相关技术的内容，想与更多大佬一起沟通，那就扫描下方二维码加入我们吧！

二、反向投影概念

        反向投影是一种记录给定图像中的像素点如何适应直方图模型像素分布的方式，简单来讲，反向投影就是首先计算某一特征的直方图模型，然后使用模型去寻找图像中存在的特征。反向投影在某一位置的值就是原图对应位置像素值在原图像中的总数目。

三、反向投影理解

        举个栗子，给大家介绍反向投影：

        想必大家都玩过一个游戏，（没玩过的可以体验一下），一个人蒙住眼睛，其余的人在指定区域内活动，蒙眼睛的人依靠声音等方式去寻找其余的人。设蒙眼睛的人为A，其余人中有个人是B。

        假如这个人只能通过声音去寻找，那这个人其实是通过“双耳效应”，简化一下，就是说当B发出声音的时候，A听到B的声音，根据自己感知到声音传到两个耳朵的不同，顺着声音的方向，做两条反向延长线，两条线交于一个点，这个点的位置，就是B所在的位置。

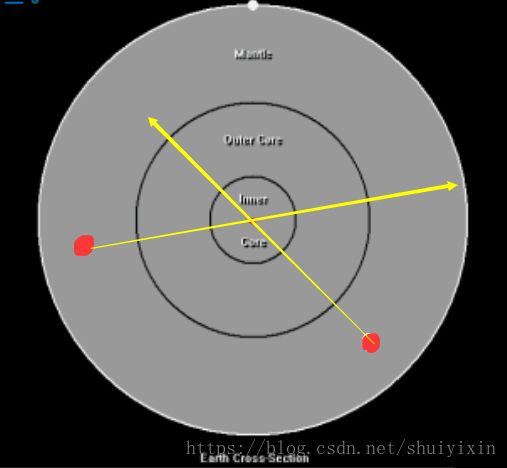
        同样原理的还有测量地震的设备，很多时候，测震源有两个设备，设备对地震源做反向投影，就会找到地震的中心。（如下图）

四、反向投影原理

 

        (1)例如灰度图像如下 ：
                Image=

                      0    1    2    3
                      4    5    6    7
                      8    9   10   11
                      8    9   14   15
        (2)该灰度图的直方图为（bin指定的区间为[0,3)，[4,7)，[8,11)，[12,16)）
                Histogram=        4    4    6    2

 

        (3)反向投影图
                Back_Projection=
                      4    4    4    4
                      4    4    4    4
                      6    6    6    6
                      6    6    2    2

 

        例如位置(0,0)上的像素值为0，对应的bin为[0,3)，所以反向直方图在该位置上的值这个bin的值4。

 

        我们看到，实际上是原图像的256个灰度值被置为很少的几个值了，具体有几个值，要看把0~255划分为多少个区间！反向投影矩阵中某点的值就是它对应的原图像中的点所在区间的灰度直方图值。所以我们可以看出，一个区间点越多，在反向投影矩阵中就越亮。

        那么怎么理解反向投影矩阵中的“反向”二字呢？从这个过程可以看出，我们是先求出原图像的直方图，再由直方图得到反向投影矩阵，由直方图到反向投影矩阵实际上就是一个反向的过程，所以叫反向。

五、反向投影作用——目标检测

        一幅图像的反向投影利用了其原始图像（或目标区域）的直方图，将该直方图作为一张查找表来找对应像素点的像素值，即将目标图像像素点的值设置为原始图像（或目标区域）直方图上对应的bin值。该bin值代表了（目标区域）上该像素值出现的概率。从而得到一幅图像的概率值。从而我们可以通过这幅概率图可以得知在这幅图像中，目标出现可能出现的位置。

六、API

1.calcBackProject函数

//1.函数原型
void cv::calcBackProject(
	const Mat *        images,
	int                nimages,
	const int *        channels,
	InputArray         hist,
	OutputArray        backProject,
	const float **     ranges,
	double             scale = 1,
	bool               uniform = true
	)

//2.参数解释
//const Mat* images:输入图像，图像深度必须位CV_8U, CV_16U或CV_32F中的一种，尺寸相同，每一幅图像都可以有任意的通道数
//int nimages : 输入图像的数量
//const int* channels : 用于计算反向投影的通道列表，通道数必须与直方图维度相匹配，第一个数组的通道是从0到image[0].channels() - 1, 第二个数组通道从图像image[0].channels()到image[0].channels() + image[1].channels() - 1计数
//InputArray hist : 输入的直方图，直方图的bin可以是密集(dense)或稀疏(sparse)
//OutputArray backProject : 目标反向投影输出图像，是一个单通道图像，与原图像有相同的尺寸和深度
//const float ranges** : 直方图中每个维度bin的取值范围
//double scale = 1 : 可选输出反向投影的比例因子
//bool uniform = true : 直方图是否均匀分布(uniform)的标识符，有默认值true

//另外两种定义

void cv::calcBackProject(
	const Mat *          images,
	int	             nimages,
	const int *	     channels,
	const SparseMat &    hist,
	OutputArray          backProject,
	const float **       ranges,
	double               scale = 1,
	bool                 uniform = true
	)

void cv::calcBackProject(
	InputArrayOfArrays             images,
	const std::vector< int > &     channels,
	InputArray                     hist,
	OutputArray                    dst,
	const std::vector< float > &   ranges,
	double                         scale
	)

2.mixChannels函数

//1.函数功能：从输入图像中拷贝某通道到输出图像中特定的通道。
//2.函数原型及参数解释：
void mixChannels(
	const Mat*src,      //一系列输入图像的数组， 被拷贝的通道的来源一系列输入图像的数组， 被拷贝的通道的来源
	size_t nsrcs,       //输入图像的个数
	Mat* dst,           //一系列目的图像的数组， 储存拷贝的通道，所有的数组必须事先分配空间（如用create），大小和深度须与输入数组等同。
	size_t ndsts,       //目的数组中图像的数目
	const int* fromTo,  //通道索引对的数组，指示如何将输入图像的某一通道拷贝到目的图像的某一通道。偶数下标的用来标识输入矩阵，奇数下标的用来标识输出矩阵。如果偶数下标为负数，那么相应的输出矩阵为零矩阵。
	size_t npairs       //fromTo中的序号对数（两个算1对）。
);

 

七、源码

#define INPUT_TITLE "Input Image"
#define OUTPUT_TITLE "Back Projection"
#define HIST_TITLE "Histogram"

#include
#include

using namespace std;
using namespace cv;



/*———————————本代码所需变量定义及初始化——————————— */
Mat src, hsv_src, hue, backProjectionImg;
int bins = 12;
int nchannels[] = { 0,0 };

/*—————————————本代码所需函数声明————————————— */
void Hist_And_BackProjection(int, void*);


int main() {
	/*—————————————全局变量的赋值————————————— */
	//1.图像载入
	src = imread("D:/hand.jpg");
	if (!src.data)
	{
		cout << "ERROR : could not load image.\n";
		return -1;
	}
	//2.将图像转化为HSV图像
	cvtColor(src, hsv_src, CV_BGR2HSV);

	//3.创建一个图像
	hue.create(hsv_src.size(), hsv_src.depth());

	//窗口命名
	namedWindow(INPUT_TITLE, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_TITLE, CV_WINDOW_AUTOSIZE);
	namedWindow(HIST_TITLE, CV_WINDOW_AUTOSIZE);

	//从输入图像中拷贝某通道到输出图像中特定的通道
	mixChannels(&hsv_src, 1, &hue, 1, nchannels, 1);

	//动态调整直方图的 bins ，并做反向投影
	createTrackbar("Histogram Bins", INPUT_TITLE, &bins, 180, Hist_And_BackProjection);
	Hist_And_BackProjection(0, 0);

	imshow(INPUT_TITLE, src);

	waitKey(0);
	return 0;
}


/*—————————————本代码所需函数实现————————————— */
void Hist_And_BackProjection(int, void*) {

	//局部变量
	float range[] = { 0,180 };
	const float *histRanges = { range };
	int hist_h = 400;
	int hist_w = 400;
	int bin_w = hist_w / bins;
	Mat h_hist;
	Mat histImage(hist_w, hist_h, CV_8UC3, Scalar(0, 0, 0));

	//直方图计算及归一化处理
	calcHist(&hue, 1, 0, Mat(), h_hist, 1, &bins, &histRanges, true, false);
	normalize(h_hist, h_hist, 0, 255, NORM_MINMAX, -1, Mat());

	//直方图反向投影
	calcBackProject(&hue, 1, 0, h_hist, backProjectionImg, &histRanges, 1, true);

	//画直方图分部图
	for (int i = 0; i < bins; i++)
	{
		/*rectangle(histImage,
			Point((i - 1)*bin_w, (hist_h - cvRound(h_hist.at(i - 1)*(400 / 255)))),
			Point(i*bin_w, (hist_h - cvRound(h_hist.at(i)*(400 / 255)))),
			Scalar(0, 0, 255),
			-1);*/

		rectangle(histImage,
			Point((i - 1)*bin_w, (hist_h - cvRound(h_hist.at(i - 1)*(400 / 255)))),
			Point(i*bin_w, hist_h),
			Scalar(0, 0, 255),
			-1);
	}

	imshow(OUTPUT_TITLE, backProjectionImg);
	imshow(HIST_TITLE, histImage);

}

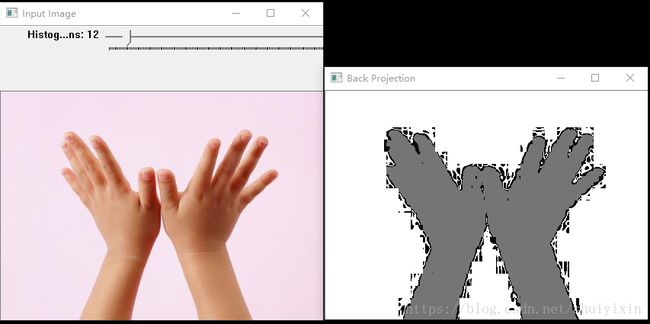
八、结果展示