卷积神经网络（CNN）相关知识以及数学推导

神经网络概述

神经元模型

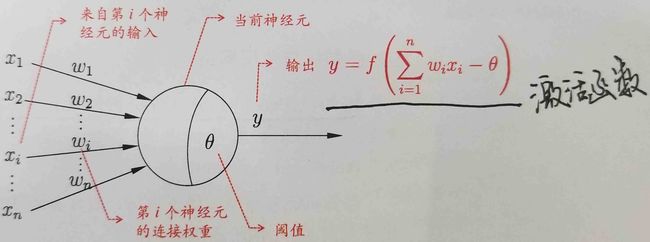
以上就是经典的“M-P神经元模型”。在这个模型中，神经元接收来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将于神经元的阈值进行比较，然后通过“激活函数”处理以产生神经元的输出。

感知机

感知机（Perceptron）是由两层神经元组成，输入层接收外界输出信号后传递给输出层，输出层是M-P神经元，也称为“阈值逻辑单元”。

感知机能够很容易的实现逻辑与、或、非运算，但是由于其只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，所以学习能力非常有限。此时就产生了多层感知机（MLP）来处理这些更加复杂的运算。

对于以上的感知机，我们可以建立模型：

f(x)=act(θT+b)

其中激活函数 act 可以使用{sign, sigmoid, tanh}之一，个人感觉这种建模方式就是将每个神经元的输入作为笛卡尔坐标系中的x轴的值，对应的输出值作为y轴上的值，通过这些已知的训练集合中的值来进行拟合，根据训练集在坐标系中的分布特征来选择不同的激活函数，也即是拟合方式的不同，就比如下面的线性回归，逻辑回归以及softmax回归。

• 激活函数使用符号函数 sign ，可求解损失函数最小化问题，通过梯度下降确定参数
• 激活函数若使用一次多项式进行拟合，就成为了线性回归，但是一般不用此种回归方法来拟合。
• 激活函数使用 sigmoid （或者 tanh ），即解决的问题为二分问题，则分类器事实上成为Logistic Regression，可通过梯度上升极大化似然函数，或者梯度下降极小化损失函数，来确定参数。
• 如果需要多分类，则事实上成为Softmax Regression。
• 如要需要分离超平面恰好位于正例和负例的正中央，则成为支持向量机（SVM）。

多层感知机

感知机存在的问题是，对线性可分数据工作良好，如果设定迭代次数上限，则也能一定程度上处理近似线性可分数据。但是对于非线性可分的数据，比如最简单的异或问题，感知器就无能为力了。这时候就需要引入多层感知器这个大杀器。

多层感知器的思路是，尽管原始数据是非线性可分的，但是可以通过某种方法将其映射到一个线性可分的高维空间中，从而使用线性分类器完成分类。下面卷积神经网络概述神经网络的大体结构图中，从X到O这几层，正展示了多层感知器的一个典型结构，即输入层-隐层-输出层。

输入层-隐层
是一个全连接的网络，即每个输入节点都连接到所有的隐层节点上。更详细地说，可以把输入层视为一个向量 x ，而隐层节点 j有一个权值向量 θj 以及偏置 bj ，激活函数使用 sigmoid 或 tanh ，那么这个隐层节点的输出应该是

fj(x)=act(θTjx+bj)

也就是每个隐层节点都相当于一个感知器。每个隐层节点产生一个输出，那么隐层所有节点的输出就成为一个向量，即

f(x)=act(Θx+b)

若输入层有 m 个节点，隐层有 n 个节点，那么 Θ=[θT] 为 n×m 的矩阵， x 为长为 m 的向量， b 为长为 n 的向量，激活函数作用在向量的每个分量上， f(x) 返回一个向量。

隐层-输出层
可以视为级联在隐层上的一个感知器。若为二分类，则常用Logistic Regression；若为多分类，则常用Softmax Regression。

解决非线性最优问题的常见算法

为讨论下面几种算法，采用最简单的线性回归作为例子。相关的参数如下（一般机器学习中都相关问题都是采用下列的参数）：
n ：训练集合的特征数量，例如房价预测中的房子的大小和卧室的数量
m ：训练样本的数量
x ：输入变量/特征
y ：输出变量/特征
(x,y) ：训练样例
ith ：训练样例的组数，表示为： (x(i),y(i))
h(x) ：拟合函数
J(x) ：损失函数

（此处注意上面推出的这个迭代式，下面要与逻辑回归中推出的迭代式进行比较）
（3）随机梯度下降法（stochastic gradient descent，SGD）
SGD是最速梯度下降法的变种。
使用最速梯度下降法，将进行N次迭代，直到目标函数收敛，或者到达某个既定的收敛界限。每次迭代都将对m个样本进行计算，计算量大。
为了简便计算，SGD每次迭代仅对一个样本计算梯度，直到收敛。伪代码如下（以下仅为一个loop，实际上可以有多个这样的loop，直到收敛）：

1、由于SGD每次迭代只使用一个训练样本，因此这种方法也可用作online learning。
2、每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。
（4）牛顿法

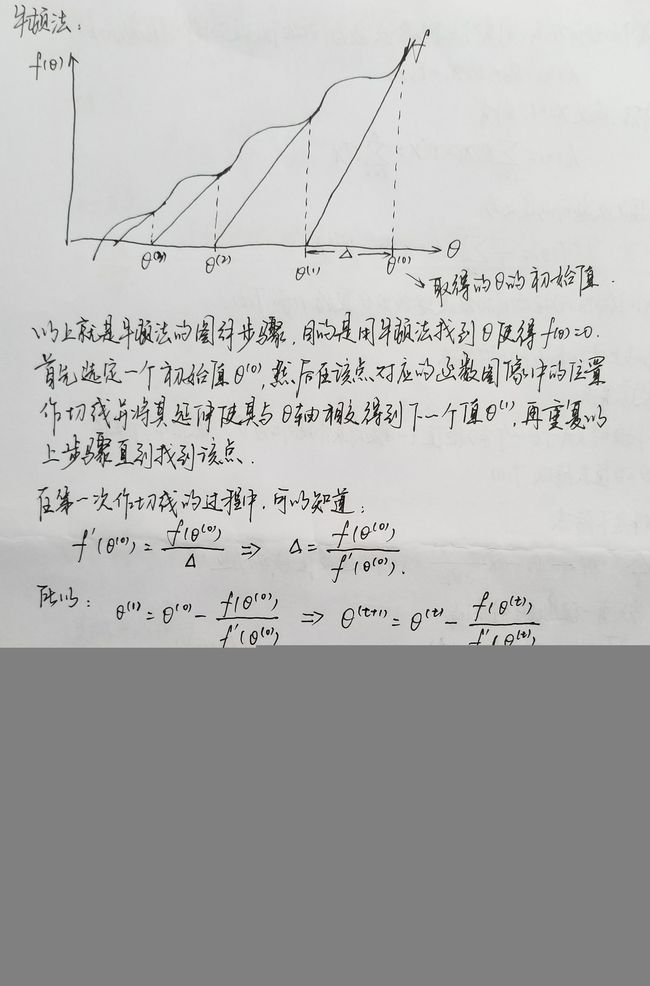
（5）高斯牛顿法
以上两种方法的详细数学推导 http://blog.csdn.net/jinshengtao/article/details/51615162

线性回归和逻辑回归

线性回归的一个具体实现可以从上面解决非线性最优问题的常见算法的例子里学习，下面首先给出一个对于线性回归的一个可能的解释。

Probabilistic Interpretation

局部加权回归（Locally weight regression，Loess/Lowess）

逻辑回归（Logistic Regression）

误差逆传播（BP）算法

通过以上的介绍我们弄清楚了神经网络的结构，常见的神经网络有多层前馈网络（每层神经元与下一层神经元全连接，神经元之间不存在同层连接，也不存在跨层连接），下面就是介绍训练类似的多层网络（即估计权重和阈值这些参数）的方法了。对于一般的问题，可以通过求解损失函数极小化问题来进行参数估计。但是对于多层感知器中的隐层，因为无法直接得到其输出值，当然不能够直接使用到其损失了。这时，就需要将损失从顶层反向传播（Back Propagate）到隐层，来完成参数估计的目标。

首先，我们给出下面的BP网络（用BP算法训练的多层前馈神经网络）：

给定训练集 D=(x1,y1),(x2,y2),……,(xm,ym),xi∈Rd,yi∈Rl ，即输入示例由 d 个属性描述，输出 l 维实值向量。为了便于讨论，上图给出了一个拥有 d 个神经元、 l 个输出神经元、 q 个隐层神经元的多层前馈网络结构，其中输出层第 j 个神经元的阈值用 θj 表示，隐层第 h 个神经元的阈值用 γh 表示。输出层第 i 个神经元与隐层第 h 个神经元之间的连接权为 νih ，隐层第 h 个神经元与输出层第 j 个神经元之间的连接权为 ωhj 。记隐层第 h 个神经元接收到的输入为 αh=∑i=1dνihxi ,输出层第 j 个神经元接收到的输入为 βj=∑qh=1ωhjbh ，其中 bh 为隐层第 h 个神经元的输出。假设隐层和输出层神经元都使用sigmoid函数。
具体推导过程如下两张图片所示：

最后补充几个常用的激活函数的导数结果：

f′(x)f′(x)f′(x)=sigmoid′(x)=f(x)(1−f(x))=tanh′(x)=1−f2(x)=softmax′(x)=f(x)−f2(x)

将以上的数学推导过程转化成伪代码为：

卷积神经网络概述

卷积神经网络沿用了普通的神经元网络即多层感知器的结构，是一个前馈网络（网络拓扑结构上不存在环或者回路）。以应用于图像领域的CNN为例，大体结构如下图所示：

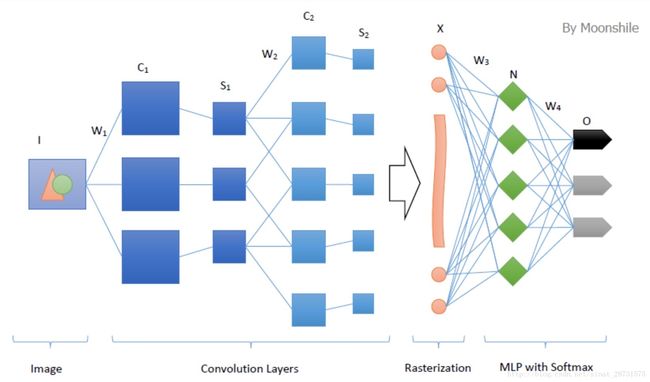
很明显，这个典型的结构分为四个大层次：

• 输入图像I。为了减小复杂度，一般使用灰度图像。当然，也可以使用RGB彩色图像，此时输入图像有三张，分别为RGB分量。输入图像一般需要归一化，如果使用sigmoid激活函数，则归一化到[0, 1]，如果使用tanh激活函数，则归一化到[-1, 1]。
• 多个卷积（C）-下采样（S）层。将上一层的输出与本层权重W做卷积得到各个C层，然后下采样（池化）得到各个S层。这些层的输出称为Feature Map。
• 光栅化（X）。是为了与传统的多层感知器全连接。即将上一层的所有Feature Map的每个像素依次展开，排成一列。
• 传统的多层感知器（N&O）。最后的分类器一般使用Softmax Regression(针对多分类问题)，如果是二分类，当然也可以使用Logistic Regression。

根据上面的基本结构，我们就逐层进行分析。

卷积层和下采样层

以上介绍的多层感知机存在一定的问题，它是一个全连接的网络，因此在输入比较大的时候，权值会特别多。比如一个有1000个节点的隐层，连接到一个1000×1000的图像上，那么就需要 10^9 个权值参数（外加1000个偏置参数）！这个问题，一方面限制了每层能够容纳的最大神经元数目，另一方面也限制了多层感知器的层数即深度。
多层感知器的另一个问题是梯度发散。一般情况下，我们需要把输入归一化，而每个神经元的输出在激活函数的作用下也是归一化的；另外，有效的参数其绝对值也一般是小于1的；这样，在BP过程中，多个小于1的数连乘，得到的会是更小的值。也就是说，在深度增加的情况下，从后传播到前边的残差会越来越小，甚至对更新权值起不到帮助，从而失去训练效果，使得前边层的参数趋于随机化（补充一下，其实随机参数也是能一定程度上捕捉到图像边缘的）。
有关神经网络训练过程中梯度的有关问题可以详细见：
https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap5/c5s0.html

既然多层感知器存在问题，那么卷积神经网络的出现，就是为了解决它的问题。卷积神经网络的核心出发点有三个。

• 局部感受野。形象地说，就是模仿你的眼睛，想想看，你在看东西的时候，目光是聚焦在一个相对很小的局部的吧？严格一些说，普通的多层感知器中，隐层节点会全连接到一个图像的每个像素点上，而在卷积神经网络中，每个隐层节点只连接到图像某个足够小局部的像素点上，从而大大减少需要训练的权值参数。举个栗子，依旧是1000×1000的图像，使用10×10的感受野，那么每个神经元只需要100个权值参数；不幸的是，由于需要将输入图像扫描一遍，共需要991×991个神经元！参数数目减少了一个数量级，不过还是太多。
• 权值共享。形象地说，就如同你的某个神经中枢中的神经细胞，它们的结构、功能是相同的，甚至是可以互相替代的。也就是，在卷积神经网中，同一个卷积核内，所有的神经元的权值是相同的，从而大大减少需要训练的参数。继续上一个栗子，虽然需要991×991个神经元，但是它们的权值是共享的呀，所以还是只需要100个权值参数，以及1个偏置参数。从MLP的 10^9 到这里的100，就是这么狠！作为补充，在CNN中的每个隐藏，一般会有多个卷积核。
• 池化。形象地说，你先随便看向远方，然后闭上眼睛，你仍然记得看到了些什么，但是你能完全回忆起你刚刚看到的每一个细节吗？同样，在卷积神经网络中，没有必要一定就要对原图像做处理，而是可以使用某种“压缩”方法，这就是池化，也就是每次将原图像卷积后，都通过一个下采样的过程，来减小图像的规模。以最大池化（Max Pooling）为例，1000×1000的图像经过10×10的卷积核卷积后，得到的是991×991的特征图，然后使用2×2的池化规模，即每4个点组成的小方块中，取最大的一个作为输出，最终得到的是496×496大小的特征图。

更加生动形象的对于这三个问题的解释可以参考以下的文章：
http://blog.csdn.net/stdcoutzyx/article/details/41596663/

现在来看，需要训练参数过多的问题已经完美解决。关于梯度发散，因为多个神经元共享权值，因此它们也会对同一个权值进行修正，积少成多，积少成多，积少成多，从而一定程度上解决梯度发散的问题！

接下来有关卷积的问题可以参考下面这两篇文章：
卷积神经网络全面解析（之前的很多内容也是参考这篇文章里面的）
以及一些有关图像语义分割的反卷积的知识：图像卷积与反卷积

Softmax Regression

指数分布族（The Exponential Family）

如果一个分布可以用如下公式表达，那么这个分布就属于指数分布族：

p(y;η)=b(y)exp(ηTT(y)−a(η))

公式中y是随机变量；
η称为分布的自然参数(natural parameter)，也称为标准参数(canonical parameter)；
T(y)称为充分统计量，通常情况下T(y)=y；
a(η)称为对数分割函数(log partition function)，本质上是一个归一化常数，确保概率和为1。

当T(y)被固定时，a(η)、b(y)就定义了一个以η为参数的一个指数分布。我们变化η就得到不同的概率分布。
在 T(y)=y 的通常情况下，η也仅仅是个实数，所以 ηTT(y) 也是实数。

下面是几个小例子：

广义线性模型（GLM）

在分类和回归问题中，我们通过构建一个关于x的模型来预测y。这种问题可以利用广义线性模型（Generalized linear models，GMLs）来解决。构建广义线性模型我们基于三个假设，也可以理解为我们基于三个设计决策，这三个决策帮助我们构建广义线性模型：

1. y|x;θ∽ExponentialFamily(η) ，假设 y|x;θ 满足一个以为参数的指数分布。例如，给定了输入x和参数θ，那么可以构建y关于η的表达式。
2. 给定x，我们的目标是要确定T(y)，即 h(x)=E[T(y)|x] 。大多数情况下 T(y)=y ，那么我们实际上要确定的是。即给定x，假设我们的目标函数是 h(x)=E[T(y)|x] 。
3. 假设自然参数η和x是线性相关，即假设： η=θTx 。

相关问题可以参考：
http://www.cnblogs.com/BYRans/p/4735409.html

多分类问题
多分类问题符合多项分布。有许多算法可用于解决多分类问题，像决策树、朴素贝叶斯等。这篇文章主要讲解多分类算法中的Softmax回归（Softmax Regression)

推导思路为：首先证明多项分布属于指数分布族，这样就可以使用广义线性模型来拟合这个多项分布，由广义线性模型推导出的目标函数 hθ(x) 即为Softmax回归的分类模型。

上面的推导过程是参考：http://www.cnblogs.com/BYRans/p/4905420.html这篇博文的，有关于Softmax回归的更多问题可以看：
Softmax回归

至此，整个卷积神经网络的相关知识就总结完了，其中参考了很多大牛们的博客，写这篇博客也是为了自己总结梳理相关的知识，本人的能力有限，如有错误的地方还请大家留言指正。