数据挖掘作业一:线性回归、逻辑回归和支持向量机
中山大学软件工程数据挖掘第一次作业
github地址:https://github.com/linjiafengyang/DataMining
官方参考答案:Answer to HW1
线性回归
某班主任为了了解本班同学的数学和其他科目考试成绩间关系,在某次阶段性测试中,他在全班学生中随机抽取1个容量为5的样本进行分析。该样本中5位同学的数学和其他科目成绩对应如下表:

利用以上数据,建立m与其他变量的多元线性回归方程。
梯度下降法代码如下:
import numpy as np
"""
梯度下降法
"""
# features scaling
def featuresNormalization(x):
x_mean = np.mean(x, axis=0) # 列均值
x_max = np.max(x, axis=0) # 列最大值
x_min = np.min(x, axis=0) # 列最小值
x_s = x_max - x_min
x = (x - x_mean) / x_s
return x, x_mean, x_s
# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
x_T = np.transpose(x)
for i in range(0, numIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# avg cost function J
cost = np.sum(loss ** 2) / (2 * m)
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(x_T, loss) / m
# update theta
theta = theta - alpha * gradient
print("Iteration %d | Theta: %s" % (i, theta))
return theta
# 数据
Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
[89, 76, 88, 93],
[89, 74, 82, 91],
[92, 71, 91, 89],
[93, 76, 89, 94]])
X, X_mean, X_s = featuresNormalization(X) # 特征值缩放
Y = np.array([89, 91, 93, 95, 97])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
n = np.alen(X[0])
alpha = 1
theta = np.zeros(n)
print(theta)
print(X)
# 6354可达到与sklearn相同的预测值
theta = gradientDescent(X, Y, theta, alpha, m, 6354)
print("Theta: ", theta)
x_predict = np.array([[88, 73, 87, 92]])
x_predict = (x_predict - X_mean) / X_s
m = np.alen(x_predict)
ones = np.ones(m)
x_predict = np.column_stack((ones, x_predict))
result = np.dot(x_predict, theta)
print("Predit result: %.4f" % result)
标准方程代码如下:
import numpy as np
Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
[89, 76, 88, 93],
[89, 74, 82, 91],
[92, 71, 91, 89],
[93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
X_T = np.transpose(X)
# theta = (X'X)^(-1)X'Y
# theta = np.dot(np.dot(np.linalg.inv(np.dot(X_T, X)), X_T), Y)
temp1 = np.dot(X_T, X)
temp2 = np.linalg.inv(temp1)
temp3 = np.dot(temp2, X_T)
theta = np.dot(temp3, Y)
print("Theta: ", theta)
x_predit = [1, 88, 73, 87, 92]
print("Predit result: ", np.dot(x_predit, theta))
正则化的标准方程代码如下:
import numpy as np
"""
正则化
"""
Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
[89, 76, 88, 93],
[89, 74, 82, 91],
[92, 71, 91, 89],
[93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
X_T = np.transpose(X)
lamda = 1
matrix = np.eye(np.alen(X))
matrix[0][0] = 0
# print(matrix)
# 无正则化
# theta = (X'X)^(-1)X'Y
# temp1 = np.dot(X_T, X)
# L2正则化
# theta = (X'X + lamda*matrix)^(-1)X'Y
temp1 = np.dot(X_T, X) + lamda * matrix
temp2 = np.linalg.inv(temp1)
temp3 = np.dot(temp2, X_T)
theta = np.dot(temp3, Y)
print("Theta: ", theta)
x_predit = [1, 88, 73, 87, 92]
print("Predit result: ", np.dot(x_predit, theta))
scikit-learn线性回归代码如下:
import numpy as np
from sklearn import linear_model
"""
scikit-learn
"""
Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
[89, 76, 88, 93],
[89, 74, 82, 91],
[92, 71, 91, 89],
[93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
model = linear_model.LinearRegression()
model.fit(X, Y)
x_predict = np.array([[1, 88, 73, 87, 92]])
result = model.predict(x_predict)
print(model.intercept_)
print(model.coef_)
print("Predit result: ", result)逻辑回归
研究人员对使用雌激素与子宫内膜癌发病间的关系进行了1:1配对的病例对照研究。病例与对照按年龄相近、婚姻状况相同、生活的社区相同进行了配对。收集了年龄、雌激素药使用、胆囊病史、高血压和非雌激素药使用的数据。变量定义及具体数据如下:
match:配比组
case:case=1病例;case=0对照(未发病)
est:est=1使用过雌激素;est=0未使用雌激素;
gall:gall=1有胆囊病史;gall=0无胆囊病史;
hyper:hyper=1有高血压;hyper=0无高血压;
nonest:nonest=1使用过非雌激素;nonest=0未使用过非雌激素;
表格略,表格的数据已在代码中体现。
简单逻辑回归代码如下:
import math
import numpy as np
from sklearn.cross_validation import train_test_split
def sigmoid(x):
result = 1 / (1 + np.exp(-x))
return result
# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
x_T = np.transpose(x)
y_T = np.transpose(y)
for i in range(0, numIterations):
hypothesis = sigmoid(np.dot(x, theta))
loss = hypothesis - y
# avg cost function J
cost = 0 - (np.sum(np.dot(y_T, np.log(hypothesis)) +
np.dot(1 - y_T, 1 - np.log(hypothesis)))) / m
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(x_T, loss) / m
# update theta
theta = theta - alpha * gradient
print("Iteration %d | Theta: %s" % (i, theta))
return theta
X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 1],
[1, 1, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 0], [1, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 1, 0, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 1, 1, 1], [0, 0, 1, 1],
[1, 0, 0, 1], [1, 0, 0, 1],
[0, 0, 0, 1], [0, 0, 0, 1],
[1, 0, 1, 1], [1, 0, 1, 1],
[0, 0, 0, 1], [0, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 1], [0, 0, 0, 0],
[0, 1, 0, 1], [0, 0, 1, 0],
[1, 1, 0, 1], [1, 1, 0, 0],
[1, 0, 0, 0], [1, 0, 1, 1]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
n = np.alen(X[0])
# 划分为训练集和测试集,测试集占1/5
X, X_test, Y, Y_test = train_test_split(X, Y, test_size=0.2)
theta = np.zeros(n)
alpha = 1
numIterations = 43000
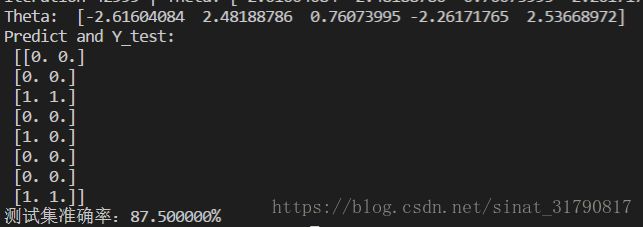
theta = gradientDescent(X, Y, theta, alpha, m, numIterations)
print("Theta: ", theta)
predict = sigmoid(np.dot(X_test, theta))
# 将小于0.5的数置为0,将大于等于0.5的数置为1
predict = np.where(predict >= 0.5, predict, 0)
predict = np.where(predict < 0.5, predict, 1)
# 统计预测准确的数目
right = np.sum(predict == Y_test)
# 将预测值和真实值放在一块,便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确率
print('测试集准确率:%f%%' % (right * 100.0 / predict.shape[0]))正则化代价函数的逻辑回归代码如下:
import math
import numpy as np
from sklearn.cross_validation import train_test_split
def sigmoid(x):
result = 1 / (1 + np.exp(-x))
return result
# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, lamda, m, numIterations):
x_T = np.transpose(x)
y_T = np.transpose(y)
for i in range(0, numIterations):
hypothesis = sigmoid(np.dot(x, theta))
loss = hypothesis - y
# avg cost function J
cost = 0 - (np.sum(np.dot(y_T, np.log(hypothesis)) + np.dot(1 - y_T, 1 - np.log(hypothesis)))) / m
+ lamda * np.sum(np.dot(theta.T, theta)) / (2 * m)
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(x_T, loss) / m
# update theta
theta = theta - alpha * (gradient + lamda * theta / m)
print("Iteration %d | Theta: %s" % (i, theta))
return theta
X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 1],
[1, 1, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 0], [1, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 1, 0, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 1, 1, 1], [0, 0, 1, 1],
[1, 0, 0, 1], [1, 0, 0, 1],
[0, 0, 0, 1], [0, 0, 0, 1],
[1, 0, 1, 1], [1, 0, 1, 1],
[0, 0, 0, 1], [0, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 1], [0, 0, 0, 0],
[0, 1, 0, 1], [0, 0, 1, 0],
[1, 1, 0, 1], [1, 1, 0, 0],
[1, 0, 0, 0], [1, 0, 1, 1]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
n = np.alen(X[0])
# 划分为训练集和测试集,测试集占1/5
X, X_test, Y, Y_test = train_test_split(X, Y, test_size=0.2)
theta = np.zeros(n)
alpha = 1
lamda = 1
numIterations = 5000
theta = gradientDescent(X, Y, theta, alpha, lamda, m, numIterations)
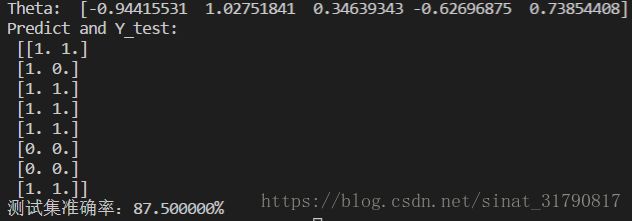
print("Theta: ", theta)
predict = sigmoid(np.dot(X_test, theta))
# 将小于0.5的数置为0,将大于等于0.5的数置为1
predict = np.where(predict >= 0.5, predict, 0)
predict = np.where(predict < 0.5, predict, 1)
# 统计预测准确的数目
right = np.sum(predict == Y_test)
# 将预测值和真实值放在一块,便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确率
print('测试集准确率:%f%%' % (right * 100.0 / predict.shape[0]))scikit-learn逻辑回归代码如下:
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import train_test_split
import numpy as np
X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 1],
[1, 1, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 0], [1, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 1, 0, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 1, 1, 1], [0, 0, 1, 1],
[1, 0, 0, 1], [1, 0, 0, 1],
[0, 0, 0, 1], [0, 0, 0, 1],
[1, 0, 1, 1], [1, 0, 1, 1],
[0, 0, 0, 1], [0, 0, 1, 1],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [0, 0, 0, 0],
[1, 0, 1, 1], [0, 0, 0, 0],
[1, 0, 0, 1], [1, 0, 1, 1],
[1, 0, 0, 1], [0, 0, 0, 0],
[0, 1, 0, 1], [0, 0, 1, 0],
[1, 1, 0, 1], [1, 1, 0, 0],
[1, 0, 0, 0], [1, 0, 1, 1]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
# 划分为训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
# 逻辑回归
model = LogisticRegression()
model.fit(X_train, Y_train)
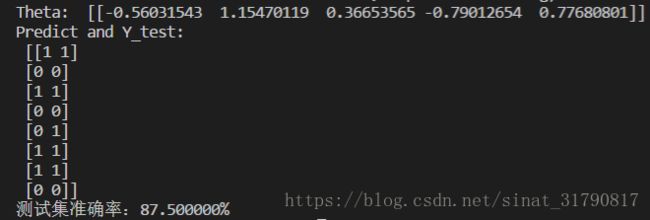
print("Theta: ", model.coef_)
# 预测
predict = model.predict(X_test)
right = sum(predict == Y_test)
# 将预测值和真实值放在一块,便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确度
print('测试集准确率:%f%%' % (right*100.0 / predict.shape[0]))
支持向量机
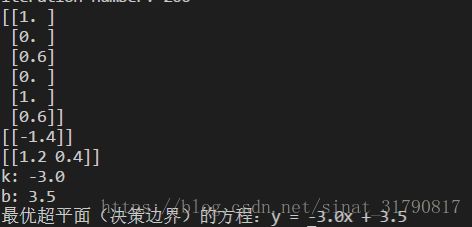
scikit-learn支持向量机代码如下:
import numpy as np
from matplotlib import pyplot as plt
from sklearn import svm
# 作图
def plot_data(X, y):
plt.figure(figsize=(10, 8))
pos = np.where(y == 1) # 找到y==1的位置
neg = np.where(y == 0) # 找到y==0的位置
# np.ravel使多维矩阵降为一维
p1, = plt.plot(np.ravel(X[pos, 0]), np.ravel(X[pos, 1]), 'rx', markersize=8)
p2, = plt.plot(np.ravel(X[neg, 0]), np.ravel(X[neg, 1]), 'bo', markersize=8)
plt.xlabel("X1")
plt.ylabel("X2")
plt.legend([p1, p2], ["y==+", "y==—"])
return plt
def SVM(X, y, kernels='linear'):
'''线性分类'''
model = svm.SVC(C=1.0, kernel='linear').fit(X, y) # 指定核函数为线性核函数
'''非线性分类'''
# model = svm.SVC(gamma=100).fit(X, y) # gamma为核函数的系数,值越大拟合的越好
plt = plot_data(X, y)
# 画线性分类的决策边界
if kernels == 'linear':
theta12 = model.coef_ # theta1 and theta2
theta0 = model.intercept_ # theta0
print("Theta 1 and theta 2: ", theta12)
print("Theta 0: ", theta0)
print("k: ", -(theta12[0, 0] * 100) / (100 * theta12[0, 1]))
print("b: ", float(-theta0 * 100 / (theta12[0, 1] * 100)))
print("最优超平面(决策边界)的方程:y = %dx + %.1f" % (-(theta12[0, 0] * 100) / (100 * theta12[0, 1]), -theta0 / theta12[0, 1]))
x1 = np.linspace(np.min(X[:, 0]), np.max(X[:, 0]), 100)
x2 = -(theta12[0, 0] * x1 + theta0) / theta12[0, 1] # theta0 + theta1*x1 + theta2*x2 == 0
plt.plot(x1, x2, 'green', linewidth=2.0)
plt.show()
# 画非线性分类的决策边界
else:
x_1 = np.transpose(np.linspace(np.min(X[:, 0]), np.max(X[:, 0]), 100).reshape(1, -1))
x_2 = np.transpose(np.linspace(np.min(X[:, 1]), np.max(X[:, 1]), 100).reshape(1, -1))
X1, X2 = np.meshgrid(x_1, x_2)
vals = np.zeros(X1.shape)
for i in range(X1.shape[1]):
this_X = np.hstack((X1[:, i].reshape(-1, 1), X2[:, i].reshape(-1, 1)))
vals[:, i] = model.predict(this_X)
plt.contour(X1, X2, vals, [0, 1], color='green')
plt.show()
X = np.array([[1, 1], [2, 2], [2, 0], [0, 0], [1, 0], [0, 1]])
y = np.array([1, 1, 1, 0, 0, 0])
plot_data(X, y)
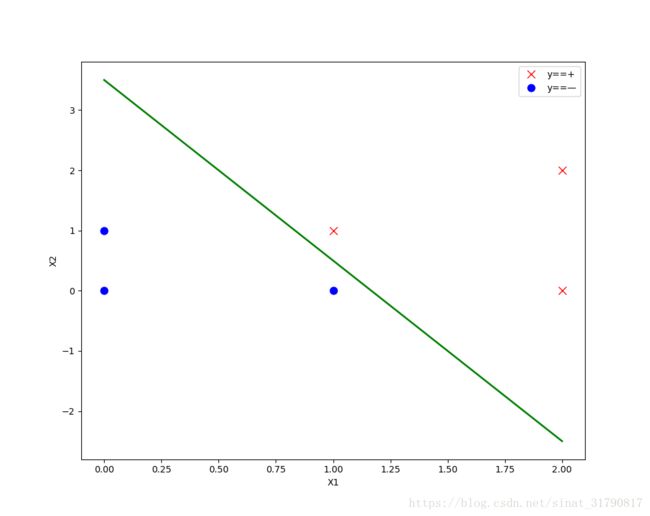
SVM(X, y) # 线性分类画决策边界
# SVM(X, y, model, class_='notLinear') # 非线性分类画决策边界拉格朗日待定乘数求解代码如下:
SMO算法来自这个博客https://blog.csdn.net/willbkimps/article/details/54697698
import numpy as np
from numpy import *
from time import sleep
from matplotlib import pyplot as plt
#加载文本文件中的数据,返回数据矩阵和类标签
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
#随机选择不等于i的值。i是第一个α的下表,m是α的数量
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
#调整大于H或小于L的α值
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
#dataMatIn, classLabels, C, toler, maxIter分别为数据集、类标签、常数C、容错率和最大迭代次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
alphas = mat(zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])
#if checks if an example violates KKT conditions
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
#将α的值调整到区间[0,C]
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print ("L==H"); continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print ("eta>=0"); continue
#对αi和αj进行修改,αi的修改量和αj相同,但方向相反
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
#the update is in the oppostie direction
#b的更新
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
alphaPairsChanged += 1
print ("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0): iter += 1
else: iter = 0
print ("iteration number: %d" % iter )
return b,alphas
dataMat,labelMat = loadDataSet('D:\linjiafengyang\Code\Python\SupportVectorMachine\smo.txt')
C = 1
toler = 0.001
maxIter = 200
b,alphas = smoSimple(dataMat, labelMat, C, toler, maxIter)
print(alphas)
print(b)
alphas = np.array(alphas)
labelMat = np.array(labelMat)
theta12 = (alphas.T*labelMat).dot(dataMat)
print(theta12)
theta0 = theta12[0,0]
theta1 = theta12[0,1]
k = -theta0 / theta1
b = -b / theta1
print("k: %.1f" % k)
print("b: %.1f" % b)
print("最优超平面(决策边界)的方程:y = %.1fx + %.1f" % (k, b))
matlab版本的SMO算法:参考这位真大佬https://blog.csdn.net/on2way/article/details/47730367,虽然代码有点小纰漏,我已经在我自己的代码改过来了:
%%
% * svm 简单算法设计
%
%% 加载数据
% * 最终data格式:m*n,m样本数,n维度
% * label:m*1 标签必须为-1与1这两类
clc
clear
close all
data = load('mydata.mat');
data = data.A;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
% 系数
b = 0;
% 松弛变量影响因子
C = 1;
iter = 0;
max_iter = 40;
%%
while iter < max_iter
alpha_change = 0;
for i = 1:num_data
%输出目标值
pre_Li = (alphas.*label)'*(data*data(i,:)') + b;
%样本i误差
Ei = pre_Li - label(i);
% 满足KKT条件
if (label(i)*Ei<-0.001 && alphas(i)i)*Ei>0.001 && alphas(i)>0)
% 选择一个和 i 不相同的待改变的alpha(2)--alpha(j)
j = randi(num_data,1);
if j == i
temp = 1;
while temp
j = randi(num_data,1);
if j ~= i
temp = 0;
end
end
end
% 样本j的输出值
pre_Lj = (alphas.*label)'*(data*data(j,:)') + b;
%样本j误差
Ej = pre_Lj - label(j);
%更新上下限
if label(i) ~= label(j) %类标签相同
L = max(0,alphas(j) - alphas(i));
H = min(C,C + alphas(j) - alphas(i));
else
L = max(0,alphas(j) + alphas(i) -C);
H = min(C,alphas(j) + alphas(i));
end
if L==H %上下限一样结束本次循环
continue;end
%计算eta
eta = 2*data(i,:)*data(j,:)'- data(i,:)*data(i,:)' - ...
data(j,:)*data(j,:)';
%保存旧值
alphasI_old = alphas(i);
alphasJ_old = alphas(j);
%更新alpha(2),也就是alpha(j)
alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
%限制范围
if alphas(j) > H
alphas(j) = H;
elseif alphas(j) < L
alphas(j) = L;
end
%如果alpha(j)没怎么改变,结束本次循环
if abs(alphas(j) - alphasJ_old)<1e-4
continue;end
%更新alpha(1),也就是alpha(i)
alphas(i) = alphas(i) + label(i)*label(j)*(alphasJ_old-alphas(j));
%更新系数b
b1 = b - Ei - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(i,:)'-...
label(j)*(alphas(j)-alphasJ_old)*data(i,:)*data(j,:)';
b2 = b - Ej - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(j,:)'-...
label(j)*(alphas(j)-alphasJ_old)*data(j,:)*data(j,:)';
%b的几种选择机制
if alphas(i)>0 && alphas(i)0 && alphas(j)iter ================== ',num2str(iter)]);
end
%% 计算权值W
W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'bo');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'r+');
hold on
%dataw = (data(index_sup,:))';
%plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面,以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
b = - b / W(2);
x = 0:0.1:2.5;
y = k*x + b;
plot(x,y,'green',x,y-1,'r--',x,y+1,'r--');
title(['松弛变量范围C = ',num2str(C)]); 运行结果如下:

决策边界(绿色线)以及支持向量(红色线)如下:

作业思考
- 线性回归与逻辑回归的区别:
线性回归主要用来解决连续值预测的问题,逻辑回归用来解决分类的问题,输出的属于某个类别的概率。 - 逻辑回归与支持向量机的区别:
两种方法都是常见的分类算法,两者的根本目的都是一样的。
目标函数:逻辑回归采用的是logistical loss,svm采用的是hinge loss。这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
训练样本点:SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
简单性:逻辑回归相对来说模型更简单,容易实现,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些。但是SVM的理论基础更加牢固,有一套结构化风险最小化的理论基础,虽然一般使用的人不太会去关注。还有很重要的一点,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算量。