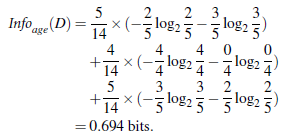机器学习之决策树（Decision Tree）及其Python代码实现

　　决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术，可以用于分析数据，同样也可以用来作预测。

　　从数据产生决策树的机器学习技术叫做决策树学习, 通俗说就是决策树。

---

　　例如，我们要对”是否要出去玩？“这样的问题进行决策的时候，通常会进行一系列的判断或者”子决策“：我们先看”OUTLOOK“，如果是天气是sunny，则我们再看空气湿度，如果是”humidity<70“（湿度小于70），那么就去玩，否则就不去玩；如果天气是overcast，那么就去玩，其他的节点可以不用判断；以此类推：

　　一般地，一颗决策树包含一个根节点，若干个 内部节点；叶节点对应与决策结果，其他每个节点对应于一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分到子节点中；根节点包含样本全集。从根节点到每个叶节点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单且直观的”分而治之“的策略，如下所示：

---

　　在建立决策树之前，我们必须先要学习一个非常重要的概念，那就是信息熵。

　　1948年，香农提出了 ”信息熵(entropy)“的概念。 一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少。

　　信息熵是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第K类样本所占的比例为[Math Processing Error]，则D的信息熵的定义为：

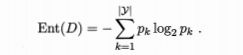
　　变量的不确定性越大，信息熵也就越大。

---

决策树归纳算法 （ID3）

　　信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)，其中 Info(D)代表没有加入A节点的所获取的信息量，Infor_A(D)代表加入A节点后所获取的信息量。
　　一般而言，信息获取量越大，则意味着使用属性A来进行划分所获得的”纯度提升“越大。因此，我们可以用信息获取量来进行决策树的划分属性的选择，著名的ID3决策树学习算法就是以信息获取量为准则来选择划分属性的。

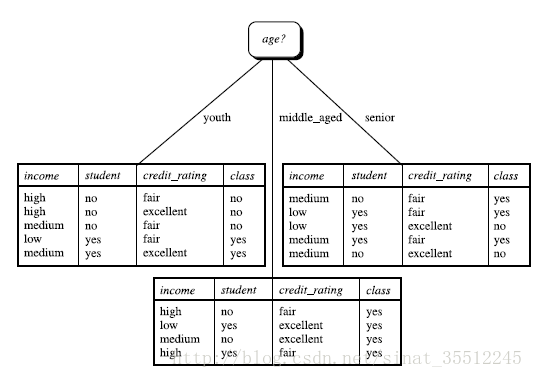
以上图中为例，

由上可得Gain(age) = Info(D) - Infor_A(D)=0.940-0.694=0.246。

类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048；

因为Gain(age)> Gain(student)>Gain(credit_rating)>Gain(income),所以，选择age作为第一个根节点。

重复以上步骤即可得出结论。

---

示例Python代码如下：

from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import tree
from sklearn import 

preprocessing
from sklearn.externals.six import StringIO

# Read in the csv file and put features into list of dict and 

list of class label
allElectronicsData = open

(r'/home/zhoumiao/MachineLearning/01decisiontree/AllElectronics.csv', 'rb')
reader = csv.reader

(allElectronicsData)
headers = reader.next()

print(headers)

featureList = []
labelList = []

for row in reader:


labelList.append(row[len(row)-1])
    rowDict = {}
    for i in range(1, len(row)-1):
        rowDict[headers[i]] = row[i]


 featureList.append(rowDict)

print(featureList)

# Vetorize features
vec = DictVectorizer()
dummyX = 

vec.fit_transform(featureList) .toarray()

print("dummyX: " + str(dummyX))
print(vec.get_feature_names())

print

("labelList: " + str(labelList))

# vectorize class labels
lb = preprocessing.LabelBinarizer()
dummyY = 

lb.fit_transform(labelList)
print("dummyY: " + str(dummyY))

# Using decision tree for classification
# clf = 

tree.DecisionTreeClassifier()
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(dummyX, 

dummyY)
print("clf: " + str(clf))


# Visualize model
with open("allElectronicInformationGainOri.dot", 'w') as f:
    f 

= tree.export_graphviz(clf, feature_names=vec.get_feature_names(), out_file=f)

oneRowX = dummyX[0, :]
print

("oneRowX: " + str(oneRowX))

newRowX = oneRowX
newRowX[0] = 1
newRowX[2] = 0
print("newRowX: " + 

str(newRowX))

predictedY = clf.predict(newRowX)
print("predictedY: " + str(predictedY))

---

其他算法：

1、C4.5: Quinlan
2、Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)

共同点：都是贪心算法，自上而下(Top-down approach)

区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

　　划分数据集的最大原则是：使无序的数据变的有序。如果一个训练数据中有20个特征，那么选取哪个做划分依据？这就必须采用量化的方法来判断，量化划分方法有多重，其中一项就是“信息论度量信息分类”。基于信息论的决策树算法有ID3、CART和C4.5等算法，其中C4.5和CART两种算法从ID3算法中衍生而来。

　　CART和C4.5支持数据特征为连续分布时的处理，主要通过使用二元切分来处理连续型变量，即求一个特定的值-分裂值：特征值大于分裂值就走左子树，或者就走右子树。这个分裂值的选取的原则是使得划分后的子树中的“混乱程度”降低，具体到C4.5和CART算法则有不同的定义方式。

　　ID3算法由Ross Quinlan发明，建立在“奥卡姆剃刀”的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。ID3算法中根据信息论的信息增益评估和选择特征，每次选择信息增益最大的特征做判断模块。ID3算法可用于划分标称型数据集，没有剪枝的过程，为了去除过度数据匹配的问题，可通过裁剪合并相邻的无法产生大量信息增益的叶子节点（例如设置信息增益阀值）。使用信息增益的话其实是有一个缺点，那就是它偏向于具有大量值的属性–就是说在训练集中，某个属性所取的不同值的个数越多，那么越有可能拿它来作为分裂属性，而这样做有时候是没有意义的，另外ID3不能处理连续分布的数据特征，于是就有了C4.5算法。CART算法也支持连续分布的数据特征。

　　C4.5是ID3的一个改进算法，继承了ID3算法的优点。C4.5算法用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足在树构造过程中进行剪枝；能够完成对连续属性的离散化处理；能够对不完整数据进行处理。C4.5算法产生的分类规则易于理解、准确率较高；但效率低，因树构造过程中，需要对数据集进行多次的顺序扫描和排序。也是因为必须多次数据集扫描，C4.5只适合于能够驻留于内存的数据集。

　　CART算法的全称是Classification And Regression Tree，采用的是Gini指数（选Gini指数最小的特征s）作为分裂标准,同时它也是包含后剪枝操作。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息，但其生成的决策树分支较大，规模较大。为了简化决策树的规模，提高生成决策树的效率，就出现了根据GINI系数来选择测试属性的决策树算法CART。

---

关于剪枝(避免过拟合（overfitting))

　　在实际构造决策树时，通常要进行剪枝，这时为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种：

先剪枝:在构造过程中，当某个节点满足剪枝条件，则直接停止此分支的构造。

后剪枝:先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

---

决策树的优缺点

优点：直观，便于理解，小规模数据集有效

缺点：1.处理连续变量不好；
　　　2.类别较多时，错误增加的比较快；
　　　3.可规模性一般。

---

参考: 机器学习经典算法详解及Python实现–决策树（Decision Tree）

参考: <<统计学习方法— 李航>>

---

机器学习系列之机器学习之Validation（验证，模型选择）

机器学习系列之机器学习之Logistic回归(逻辑蒂斯回归）