机器学习 线性回归和矩阵的运算
线性回归
线性回归:
线性回归:寻找一种能预测的趋势
线性关系:
二维:直线关系
三维:特征。目标值,平面中
线性关系定义:
y=kx+b
b为偏置。为了是对于单个特征的情况更加通用。
线性关系模型:
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10)
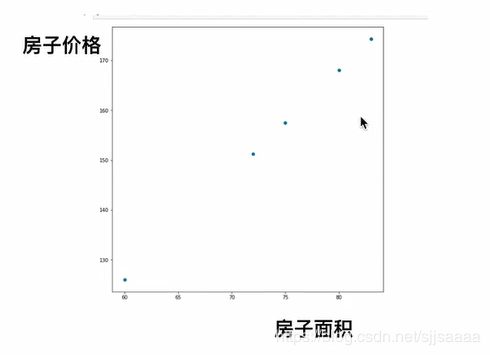
plt.scatter([60,72,75,80,83],[126,151.2,157.5,168,174.3])#绘制散点图
plt.show()
矩阵的运算
import numpy as np
a=[[1,2,3,4],[5,6,7,8],[2,3,7,9]]
b=[2,2,2,2]
np.multiply(a,b)
import numpy as np
a=[[1,2,3,4],[5,6,7,8],[2,3,7,9]]
b=[[2],[2],[2],[2]]
np.dot(a,b)
矩阵运算就是为了满足线性回归运算的需求。