斯坦福CS224N_自然语言处理NLP深度学习DL课程笔记（一）

Lecture 1: Introduction

pdf

本节课是对自然语言处理的定义介绍和应用介绍，还顺带说了NLP的难点；
本节课使用深度学习作为NLP的主要处理工具。

传统的机器学习技术，需要人为地去做特征工程，将这些的特征喂给机器学习算法；然后机器学习算法去训练，来找到最拟合训练数据+正则化损失最小的权重。教授说，我们的传统机器学习技术，其实主要是在做数值优化的问题。

人为设计的特征具有如下缺点：

• over-specified，过于具体的
• incomplete. 不够完整的
• take a long time to design and validate 需要长时间的设计和验证

深度学习是机器学习的一个子域。它使用算法，让机器能够自动地学习特征；我们只需要将最原生的特征喂给深度学习算法，它就可以自己学习特征，自己分类，表现得很好。

经常用到的英文术语：

linguistics 语言学
taxonomy 分类

推荐的阅读文献：

Deep Learning in Neural Networks: An Overview

Lecture 2: Word Vectors

2018-pdf
2017-pdf

2.1 Word meaning 词的含义

webster dictionary 韦氏字典
denotation 表示、含义
synonym sets 同义词集
hypernyms 统称、抽象（“is-a”关系）例：Color is a hypernym of red， red is a type of color.
nuance 细微差别
human labor 人类劳动
orthogonal 正交
dense vector 密集的矢量

在语言学中，词的含义就是通过这个词所传达的具体的指代，或人的想法和意志。可以用如下公式表示：
$$signifier(symbol)⟺signified(ideaorthing)$$
这样一个转换叫做指代$denotion$。

在计算机中有三种方式去表示词/词的有用信息：

• 类似WordNet的资源库
• 离散化的符号例如“one-hot encoding”
• 利用“distributional similarity”分布相似性

下面分别说下这三种方法。

2.1.1 Use resources like WordNet

WordNet是一个包含了词的同义词和上级词的很大的资源库。

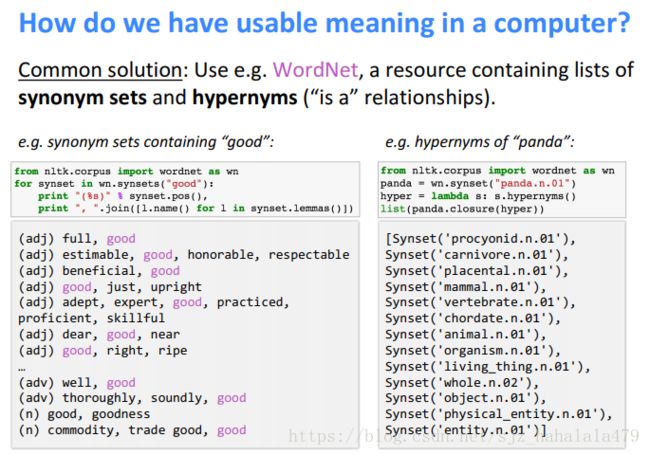
如果让计算机使用wordnet的方法获取词义会有一些问题：

1. 词在不同的情况下有不同的同义词，但计算机并不知道如何区分使用环境。例如上图中的"good"，它有表示专业上熟练的同义词“proficient”，也有表示食物熟了的同义词"wipe"，但是"proficient"和"wipe"并不是同义词。
2. 人类的语言是不断进化的，资料库不能保证永远up-to-date。
3. 资料库是主观的，而且需要大量的人类精力来维护。
4. 计算机不好根据资料库来计算词之间的相似度。

2.1.2 Use Discrete Symbols

传统NLP中，我们会使用离散的符号表示离散的词语。比如，独热编码。

利用独热编码，将每个词汇都表示为一个向量。向量的维度是词汇表中词语的数量。

我们纵然可以使用这种方法来计算，包含不同词语的语言文本之间的相似性。但是，计算机仍然不懂这些词语的意思。由于词与词之间是正交的，点积的结果是0，计算机也无法计算词语之间的相似性。

那么我们自然而然想到的解决方式有两种：

• 一种是利用资料库，我们再做一个巨大的表示词与词相关性的矩阵
• 第二种是，我们能否利用表示一个词的向量本身，来去编码词与词的相关性。

2.1.3 Use Distributional Similarity

根据词汇语义理论中的相似性分布是上一节中第二种解决方式的延伸。

它的核心想法是：一个词语的意义是由文本内容中它邻近的其它词赋予的。考虑上图中banking的例子，它的意义就是有和它一起出现的gorvenment, debt problem, Europe等词赋予的。

2.2 Word2Vec: Introduction

corpus 语料库
A simple but tough-to-best baseline for sentence embeddings iclr,2017

在开始的时候，我们介绍一下神经网络词嵌入的一个通用方法。我们希望定义一个模型。它通过词向量，基于中心词$w_t$，来预测中心词的上下文词汇：
$$p(content|w_t)$$
由此，我们可以定义一个损失函数$J$:
$$J=1-p((content|w_t))$$
我们需要通过一些手段，使损失函数降到最低。

神经网络的历史中，关于直接学习低维词向量的目标，有一些比较经典的论文：

现在说回Word2Vec，Word2Vec是一个学习词向量的框架，由谷歌在2013年首次提出。
它的基本想法是：

• 有一个巨大的文本语料库
• 在固定的词汇表中，每个词都可以表示为1个向量
• 对文本的每个位置t进行遍历，每个t上都有中心词c，和上下文词o。
• 我们可以根据c和o的相似性，来计算给定c的情况下产生o的概率
• 我们需要不断调整词向量来最大化概率

本节课重点介绍两种算法：

• skip-gram 算法
• continuous bag of words算法

还有两种有效的训练方法：

• Hierarchical softmax
• Negative sampling

目标函数

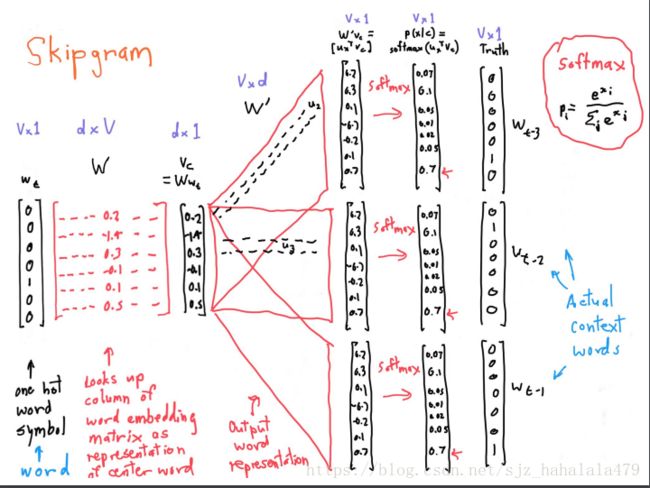
给定超参数m作为窗口的固定大小，对于文本的每个位置t，基于中心词$w_t$（图片笔误），预测上下文词汇。
所以目标函数就是每个位置的窗口的每个上下文词汇概率的连乘。
$$L(\theta )=\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}p(w_{t+j}|w_t;\theta )$$
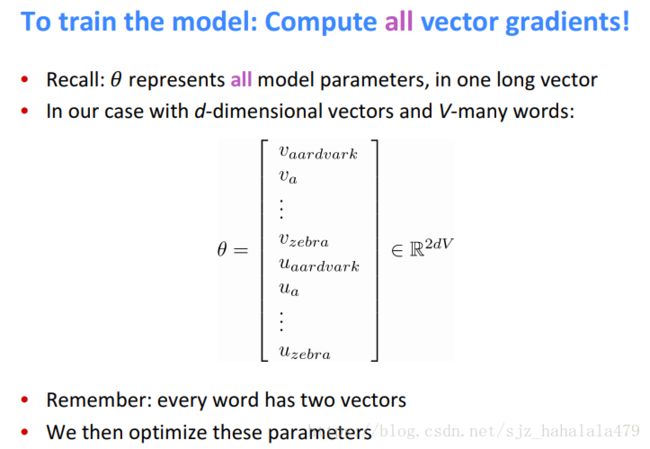
注意$\theta$代表的参数，是我们所有的词向量。

由于直接计算连乘概率十分不友好，我们将$L(\theta )$取对数，再进行normalization，然后取负，得到$L(\theta )$的负对数似然$J(\theta )$。

术语：loss function = objective function = cost function
似然函数的损失计算一般是：交叉熵损失

如何计算$p(w_{t+j}|w_t;\theta )$呢？
一种简单的方法是使用softmax函数。我们对每个词$w$，都使用两个向量来表示。一个向量$v_w$是它作为中心词时的向量；另一个向量$u_w$是它作为上下文时的向量。
那么对于中心词(记做c)和上下文词(记做o)，有
$$P(o|c)=\frac{exp({u_o}^T{v}_c)}{{\sum }_{w\in V}exp(u_w^T{v}_c)}$$

softmax 函数可以将任意的实值$x_i$映射到概率分布$p_i$上，它有两个特点：

• “max”由于指数函数的特性，大的数映射后会更大，所以softmax对最大的$x_i$有放大作用
• “soft”是指，它仍然会分一点概率给小的值

skip-gram的流程如下：

关于$\theta$的解释：

2.3 Derivations of gradient 梯度的推导

本节使用纯数学推导梯度，原式为：
$$P(o|c)=log(\frac{exp({u_o}^T{v}_c)}{{\sum }_{w\in V}exp(u_w^T{v}_c)})$$
我们需要计算$\theta$中所有参数的梯度，先以计算$\frac{\partial P}{\partial v_c}$为例。

首先：
$$\begin{gathered} \frac{\partial P}{\partial v_c}=\frac{\partial }{\partial v_c}log(exp({u_o}^T{v}_c)-\frac{\partial }{\partial v_c}log(\sum _{w=1}^{T}exp(u_w^T{v}_c)) \\ =\frac{\partial }{\partial v_c}({u_o}^T{v}_c)-\frac{\partial }{\partial v_c}log(\sum _{w=1}^{T}exp(u_w^T{v}_c))(1) \end{gathered}$$

求梯度时，有个很有用的tip:
$$\frac{\partial x^{T}a}{\partial x}=\frac{\partial a^{T}x}{\partial x}=a$$

so，(1)式减号左边的项简化为$u_o$，右边的项需要应用链式法则。
令
$$Z=\sum _{w=1}^{T}exp(u_w^T{v}_c)$$
右边的项变为：
$$F=log(Z)$$
则，
$$\frac{\partial F}{\partial v_c}=\frac{\partial F}{\partial Z}\cdot \frac{\partial Z}{\partial v_c}=\frac{1}{Z}\cdot \frac{\partial Z}{\partial v_c}$$

$\frac{\partial Z}{\partial v_c}$计算如下：
$$\begin{gathered} \frac{\partial Z}{\partial v_c}=\frac{\partial }{\partial v_c}\sum _{w=1}^{T}exp(u_w^T{v}_c) \\ =\sum _{w=1}^T\frac{\partial }{\partial v_c}exp(u_w^T{v}_c)(2) \end{gathered}$$
对(2)再应用一些链式法则：
令
$$Q_w=u_w^T{v}_c$$
，那么
$$\frac{\partial Z}{\partial v_c}=\frac{\partial Z}{\partial Q}\cdot \frac{\partial Q}{\partial v_c}$$

(2)式中，
$$\begin{gathered} \frac{\partial Z}{\partial Q}=\frac{\partial }{\partial Q}\sum _{w=1}^{T}exp(Q_w) \\ =\sum _{w=1}^T\frac{\partial }{\partial Q}exp(Q_w) \\ =\sum _{w=1}^{T}exp(Q_w) \end{gathered}$$
所以，
$$\begin{gathered} \frac{\partial Z}{\partial v_c}=\frac{\partial Z}{\partial Q}\cdot \frac{\partial Q}{\partial v_c} \\ =\sum _{w=1}^{T}exp(Q_w)\cdot u_w \\ =\sum _{w=1}^{T}exp(u_w^T{v}_c)\cdot u_w \end{gathered}$$

那么，
$$\begin{gathered} \frac{\partial F}{\partial v_c}=\frac{1}{Z}\cdot \frac{\partial Z}{\partial v_c} \\ =\frac{{\sum }_{w=1}^{T}exp(u_w^T{v}_c)\cdot u_w}{Z} \\ =\frac{{\sum }_{w=1}^{T}exp(u_w^T{v}_c)\cdot u_w}{{\sum }_{w=1}^{T}exp(u_w^T{v}_c)}(3) \end{gathered}$$
式中，分子的w和分母的w不可消去，为避免混淆，用另一个字母代替：
$$\begin{gathered} \frac{{\sum }_{x=1}^{T}exp(u_x^T{v}_c)\cdot u_x}{{\sum }_{w=1}^{T}exp(u_w^T{v}_c)} \\ =\sum _{x=1}^T\frac{exp(u_x^T{v}_c)\cdot u_x}{{\sum }_{w=1}^{T}exp(u_w^T{v}_c)} \\ =\sum _{x=1}^{T}p(x|c)\cdot u_x \end{gathered}$$
所以，最终梯度的推导式为：
$$\frac{\partial P}{\partial v_c}=u_o-\sum _{x=1}^{T}p(x|c)\cdot u_x$$

实际上，梯度可以看作，我们观察到的上下文当前的词向量，减去所有文本的期望。

上文提到，我们不仅需要对每个center word求偏导，还要对context word求偏导。

2.4 Cost/Objective functions

上节演示了梯度的计算，这节我们要思考如何根据梯度优化我们的目标函数。
一般是采用梯度下降（GD）的方法优化。

写成矩阵形式：
$${\theta }^{new}={\theta }^{old}-\alpha {\nabla }_{\theta }J(\theta )$$
对$\theta$中的每个元素${\theta }_j$来说，
$${\theta }_j^{new}={\theta }_j^{old}-\alpha \frac{\partial }{\partial {\theta }_j^{old}}\theta J({\theta }_j)$$

def func1():
  while True:
    theta_grad = evaluate_gradient(J,corpus,theta)
    theta_new = theta_old = alpha * theta_grad

每次对$\theta$中所有元素进行优化非常耗时，所以实践中每次epoch，只对随机选取的一小撮${\theta }_j$进行优化，叫做随机梯度下降(SGD)。

def func2():
  while True:
    window = sample_window(cprpus)
    theta_grad = evaluate_gradient(J,window,theta)
    theta_new = theta_old = alpha * theta_grad