程序实现黎曼和(定积分)

想象一下，如果你手里有一块形状不规则的土地（实际上我没有，穷…），要测量它的面积，怎么办呢？

拿尺子量，不知如何下手，突然感觉高中几何解决不了，得祭出本科的高等数学才行。所以，惯例我们应该发扬拿来主义，比如 “国际上，如何如何…”：

一个叫黎曼的德国数学家（Bernhard Riemann, 1826-1866），他想了个办法：将这不规则图形切成一条条的小长条儿，然后将这个长条近似的看成一个矩形，再分别测量出这些小矩形的长度，再计算出它们的面积，把所有矩型面积加起来就是这块不规则地的面积。这就是著名的“黎曼和”。小长条宽度趋于0时，即为面积微分，各个面积求和取极限即为定积分。虽然牛顿时代就给出了定积分的定义，但是定积分的现代数学定义却是用黎曼和的极限给出。

好吧，大致意思是理解了，光说不行，得练习。于是我先造出来一块地来当地主，就当下图绿色部分是我的地吧

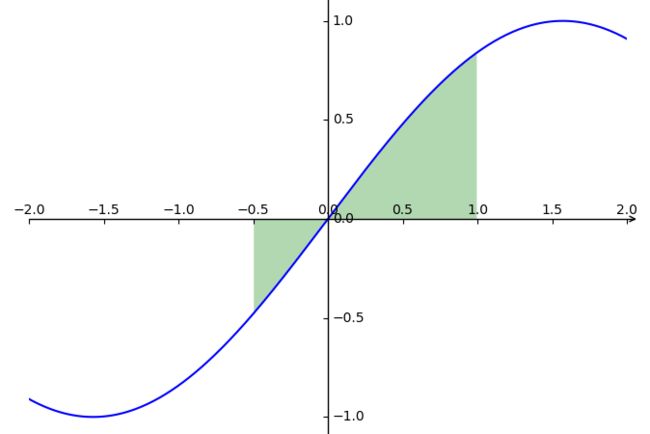
谁家能把土地划成这样啊，好吧，承认是为了一会切割小矩形的时候，方便计算高而特意用了正弦曲线，否则要是一点曲线规律都没有，那真的要用尺子去一个个量小矩形的高了，累死。

计算正弦曲线封闭区间和y轴相封存的面积

言归正传，说一下应用题的要求吧。

如上图的曲线是一个sin正弦函数，公式 y=sin(x)，我们要求的是这个函数与x轴闭区间[-0.5,1.0]所夹的部分面积，也就是绿色部分。

按照定积分的分割方法，我们把这片面积分割成n个小矩形，挨个计算面积，累加求和就是大约绿色部分的总面积了。分割的n越多，越接近于真实面积，但是计算量也会增大；反之分割的越少越省事，但是精度就下降了。大致如下图这般：

用python画了个示意图，以表明积分的原理

#include 
#include 

// 求曲线面积(定积分)。参数为，函数f(x)，x轴上区间[begin,end]两个点的值
// @param begin    x轴区间开始位置
// @param end      x轴区间结束位置
float integration(float begin, float end)
{
  float sum = 0;         //所有矩形的面积累加总和
  float n = 1000;        //将函数曲线下方划为n个矩形，n值越大，精确值越高
  float width = (end - begin) / n;  //单个矩形宽度，函数总长度除以矩形数量得到
  for(float i=1 ; i <= n ; i++)     //计算每个矩形的面积
  {
    float x = begin + width * i;     //通过i的递增，得出每个矩形底部x点的值
    float y = fabs(sin(x));
    float area = y * width; //求x点对应的y值，取绝对值后，得到高度；再用底宽度乘高得出单个矩形面积
    sum += area;         //累加矩形面积
  }
  return sum;
}

int main(){
  printf("sin(x), x range is: [-0.5 , 1.0], area is: %f\n", integration(-0.5 , 1));
  return 0;
}

编译执行

$ g++ test.cpp
$ ./a.out
sin(x), x range is: [-0.5 , 1.0], area is: 0.582387

得出面积大概是0.582387。

到这里又开始有疑问了，如何验证正确率？

那么，我该祭出不定积分公式了，面积

$$A={\int }_a^{b}f(x)dx$$

则对公式进行推导出其原函数，然后限定[a,b]的区间，就是定积分了，求面积。

按上图，积分函数f(x)=sin(x)，公式为。
$$A={\int }_a^{b}sin(x)dx$$
把原函数找出来
$$A=(-cos(x)+C){|}_a^b$$
上限b减去下限a，展开后常数C抵消了，最终成了
$$A=cos(a)-cos(b)$$

设置定积分下限a=-0.5，上线b=1.0。但是结果却错了，算下来0.3多，和我们上面的0.5多相差太大。原来看图，就明白了，图是两块啊，分布在y轴两侧，不能直接这么算，应该拆分一下，变成[-0.5,0]和[0,1]两个区间，分别运用上面的公式计算，并取绝对值

$$A=|cos(-0.5)-cos(0)|+|cos(0)-cos(1)|=0.582114$$

怎么样，我们用代码堆叠小方块算出来的0.582387，是不是很接近用公式计算出来的结果0.582114？只相差了0.000273。

另外一个验证的方式，用高大上的在线定积分计算器 https://zh.numberempire.com/definiteintegralcalculator.php 核对下，输入函数是sin(x)，自变量x从-0.5到0，结果是 −0.122417，取绝对值后是 0.122417；然后自变量x再输入0到1，结果是 0.459697，两者相加得到 0.582114。

计算圆的面积

为了更好直观的说明原理，我又换了一个容易计算的图，如下

这次，圆的函数方程式为 $r^2=(x-a{)}^2+(y-b{)}^2$ 可以用这个来计算x和y的关系，a、b是圆心坐标。

对于面积，我们有公式 $s=\pi r^2$ 就可以推算出，再除以2就是半圆的面积。计算下来，大概是6.2831852。

接下来，我们继续用上文的求定积分的方式，结合圆的函数方程式，计算出半圆面积。

#include 
#include 

// 求曲线面积(定积分)。参数为，函数f(x)，x轴上区间[begin,end]两个点的值
// @param begin    x轴区间开始位置
// @param end      x轴区间结束位置
float integration(float begin, float end)
{
  float r = 2;
  float a = 0;
  float b = 0;
  float sum = 0;         //所有矩形的面积累加总和
  float n = 1000;        //将函数曲线下方划为n个矩形，n值越大，精确值越高
  float width = (end - begin) / n;  //单个矩形宽度，函数总长度除以矩形数量得到
  for(float i=1 ; i <= n ; i++)     //计算每个矩形的面积
  {
    float x = begin + width * i;     //通过i的递增，得出每个矩形底部x点的值
    float y = sqrt(r*r - (x-a)*(x-a)) + b;
    float area = y * width; //求x点对应的y值，取绝对值后，得到高度；再用底宽度乘高得出单个矩形面积
    sum += area;         //累加矩形面积
  }
  return sum;
}

int main(){
  printf("circle, x range is: [-2.0 , 2.0], area is: %f\n", integration(-2.0 , 2.0));
  return 0;
}

编译运行得到结果

circle, x range is: [-2.0 , 2.0], area is: 6.282976

这和我们用公式计算出来的结果6.2831852，只相差了0.0002092，万分之2的差距，精度还可以。

接下来我们调高精度n，设置成10000，计算后的结果是 6.283169，相差了0.0000162，这次是10万分之一。

我们再调低精度n，到100，计算后的结果是 6.276536，这次相差0.0066492，差距拉大到千分之六了。

附录

上文中的几个图像，我都是用python绘制出来，奉上python画图的源码。

1. 正弦函数的图

import matplotlib.pyplot as plt
import numpy as np
import mpl_toolkits.axisartist as axisartist

#创建画布
fig = plt.figure(figsize=(8, 8))
#使用axisartist.Subplot方法创建一个绘图区对象ax
ax = axisartist.Subplot(fig, 111)
#将绘图区对象添加到画布中
fig.add_axes(ax)


# 通过set_visible方法设置绘图区所有坐标轴隐藏
ax.axis[:].set_visible(False)

# 添加x坐标轴，且加上箭头
ax.new_floating_axis
ax.axis["x"] = ax.new_floating_axis(0,0)
ax.axis["x"].set_axisline_style("->", size = 1.0)

# 添加y坐标轴，且加上箭头
ax.axis["y"] = ax.new_floating_axis(1,0)
ax.axis["y"].set_axisline_style("-|>", size = 1.0)

# 设置x、y轴上刻度显示方向
ax.axis["x"].set_axis_direction("top")
ax.axis["y"].set_axis_direction("right")


#设置x、y坐标轴的范围
plt.xlim(-2,2)
plt.ylim(-1.5,1.5)


#plt.grid() # 网格线
plt.legend(loc="upper left") # 图例说明，loc指定位置


#生成x步长为0.1的列表数据
x = np.linspace(-4, 4, 800)
y = np.sin(x)

#x - array( length N) 定义曲线的 x 坐标
#y - array( length N ) 定义曲线的 y 坐标
#如果数据点比较少的情况下，会有缝隙出现，使用interpolate可以填充缝隙
plt.fill_between(x, y, where=(-0.5<=x) & (x<=1), facecolor='green', alpha=0.3, interpolate=True)

# 绘制填充红色的矩形方块，以展示积分的直观图
qujian = x[np.where((-0.5<=x) & (x<=1))]
i = 5
for xi in qujian:
  if i > 5 :
    rect = plt.Rectangle((xi,0),0.04,np.sin(xi)+0.02, color='red') # 之所以给加了个+0.02，是对画出来的图微微调整，更好看些。
    ax.add_patch(rect)
    i = 0
  i = i + 1

#绘制图形
plt.plot(x,y, c='b')

plt.show()

注意上面的“绘制填充红色的矩形方块”部分的代码，如果不想绘制方块，只看原图的话，把这部分代码注释掉就行。

2. 圆形图

这里上下文和上文绘制正弦函数是一样的，只把核心画圆部分贴出来，覆盖之前画正弦函数的部分就行了

......
plt.legend(loc="upper left") # 图例说明，loc指定位置

# 圆的基本信息
# 1.圆半径
r = 2.0
# 2.圆心坐标
a, b = (0., 0.)
theta = np.arange(0, 2*np.pi, 0.01)
x = a + r * np.cos(theta)
y = b + r * np.sin(theta)
plt.plot(x, y) # 画圆
plt.axis('equal')

#x - array( length N) 定义曲线的 x 坐标
#y - array( length N ) 定义曲线的 y 坐标
#如果数据点比较少的情况下，会有缝隙出现，使用interpolate可以填充缝隙
plt.fill_between(x, y, where=(-r<=x) & (x<=r) & (y>=0), facecolor='green', alpha=0.3, interpolate=True)


# 绘制填充红色的矩形方块，以展示积分的直观图
qujian = np.linspace(-r, r, 400)
i = 5
for xi in qujian:
  if i > 5 :
    y = np.sqrt([(r*r - (xi-a)*(xi-a))]) + b # 根据圆的公式 r^2 = (x-a)^2 + (y-b)^2 推算出y
    rect = plt.Rectangle((xi-0.02,0), 0.04, y, color='red') # 画矩形的时候有点偏差，所以往左移了0.02。
    ax.add_patch(rect)
    i = 0
  i = i + 1

plt.show()

3. 除了正弦函数，我还写了余弦、指数等函数的面积计算

#include 
#include 

// 求曲线面积(定积分)。参数为，函数f(x)，x轴上区间[begin,end]两个点的值
// @param f(float) 这个参数是'函数指针'传值，传递的是一个函数的地址；这个函数用来求x轴上某一点对应的y值。
// @param begin    x轴区间开始位置
// @param end      x轴区间结束位置
float integration(float f(float), float begin, float end)
{
  float sum = 0;         //所有矩形的面积累加总和
  float n = 1000;        //将函数曲线下方划为n个矩形，n值越大，精确值越高
  float width = (end - begin) / n;  //单个矩形宽度，函数总长度除以矩形数量得到
  for(float i=1 ; i <= n ; i++)     //计算每个矩形的面积
  {
    float x = begin + width * i;     //通过i的递增，得出每个矩形底部x点的值
    float area = fabs(f(x)) * width; //求x点对应的y值，取绝对值后，得到高度；再用底宽度乘高得出单个矩形面积
    sum += area;         //累加矩形面积
  }
  return sum;
}

// 第一个例子，函数f(x)为正弦曲线
float function1(float x){
  return sin(x);
}

// 第二个例子，函数f(x)为余弦曲线
float function2(float x){
  return cos(x);
}

// 第三个例子，函数f(x)为指数曲线
float function3(float x){
  return exp(x);
}

int main(){
  printf("sin(x), x range is: [-0.5 , 1.0], area is: %f\n", integration(function1, -0.5 , 1));
  printf("cos(x), x range is: [-1.0 , 1.0], area is: %f\n", integration(function2, -1 , 1));
  printf("exp(x), x range is: [ 0.0 , 2.0], area is: %f\n", integration(function3, 0 , 2));
  return 0;
}

编译执行

$ g++ test.cpp
$ ./a.out
sin(x), x range is: [-0.5 , 1.0], area is: 0.582387
cos(x), x range is: [-1.0 , 1.0], area is: 1.682942
exp(x), x range is: [ 0.0 , 2.0], area is: 6.395446

始于 2019-11-01，北京；更于 2019-11-02，北京。

该文章在以下平台同步

• HICOOL.TOP: https://www.hicool.top/article/5dbbfdae289f2348859bee3e
• CSDN:
• 简书: