自然语言处理NLP中的N-gram模型
自然语言处理NLP中的N-gram模型
文章目录
- 自然语言处理NLP中的N-gram模型
- @[toc]
- Naive Bayes
- N-gram
- N-gram简介
- N-gram中的概率计算
- N-gram的用途
- 用途一:词性标注
- 用途二:垃圾短信分类
- 用途三:分词器
- 用途四:机器翻译和语音识别
- 机器翻译
- 语音识别
- N-gram中N的确定
- N-gram中的数据平滑方法
- 拉普拉斯平滑
- Add-one
- Add-K
- 内插与回溯
- 内插
- 回溯
- Absolute Discounting
- Kneser-Ney Smoothing
- N-gram对训练数据集的要求
- N-gram的进化版:NNLM
- NNLM的进化版:RNNLM
- Word2Vec
- 参考资料
文章目录
- 自然语言处理NLP中的N-gram模型
- @[toc]
- Naive Bayes
- N-gram
- N-gram简介
- N-gram中的概率计算
- N-gram的用途
- 用途一:词性标注
- 用途二:垃圾短信分类
- 用途三:分词器
- 用途四:机器翻译和语音识别
- 机器翻译
- 语音识别
- N-gram中N的确定
- N-gram中的数据平滑方法
- 拉普拉斯平滑
- Add-one
- Add-K
- 内插与回溯
- 内插
- 回溯
- Absolute Discounting
- Kneser-Ney Smoothing
- N-gram对训练数据集的要求
- N-gram的进化版:NNLM
- NNLM的进化版:RNNLM
- Word2Vec
- 参考资料
Naive Bayes
首先我们复习一下一个非常基本的模型,朴素贝叶斯(Naive Bayes)。朴素贝叶斯的关键组成是贝叶斯公式与条件独立性假设。为了方便说明,我们举一个垃圾短信分类的例子。
上面这句话抄自我手机中的一条垃圾短信,自从去过澳门,手机就时不时收到这样的关于赌场的短信。朴素贝叶斯模型就是要衡量这句话属于垃圾短信敏感句子的概率,我们以前半句为例:
p ( 垃 圾 短 信 ∣ " 在 家 日 赚 百 万 " ) ∝ p ( 垃 圾 邮 件 ) p ( " 在 家 日 赚 百 万 " ∣ 垃 圾 短 信 ) p(垃圾短信|"在家日赚百万")\propto p(垃圾邮件)p("在家日赚百万"|垃圾短信) p(垃圾短信∣"在家日赚百万")∝p(垃圾邮件)p("在家日赚百万"∣垃圾短信)
由条件独立性假设:
p ( " 在 家 日 赚 百 万 " ∣ J ) = p ( " 在 " , " 家 " , " 日 " , " 赚 " , " 百 " , " 万 " ∣ J ) = p ( " 在 " ∣ J ) p ( " 家 " ∣ J ) p ( " 日 " ∣ J ) p ( " 赚 " ∣ J ) p ( " 百 " ∣ J ) p ( " 万 " ∣ J ) p("在家日赚百万"|J)=p("在","家","日","赚","百","万"|J)\\ =p("在"|J)p("家"|J)p("日"|J)p("赚"|J)p("百"|J)p("万"|J) p("在家日赚百万"∣J)=p("在","家","日","赚","百","万"∣J)=p("在"∣J)p("家"∣J)p("日"∣J)p("赚"∣J)p("百"∣J)p("万"∣J)
上面每一项条件概率都可以通过在训练数据的垃圾短信中统计每个字出现的次数得到,然而这里有一个问题,朴素贝叶斯将句子处理为一个**词袋模型(Bag-of-Words, BoW)**,以至于不考虑每个单词的顺序。这一点在中文里可能没有问题,因为有时候即使把顺序捣乱,我们还是能看懂这句话在说什么,但有时候不行,例如:
那么有没有模型是考虑句子中单词之间的顺序的呢?有,N-gram就是。
N-gram
N-gram简介
在介绍N-gram之前,让我们回想一下**“联想”**的过程是怎样发生的。如果你是一个玩LOL的人,那么当我说“正方形打野”、“你是真的皮”,“你皮任你皮”这些词或词组时,你应该能想到的下一个词可能是“大司马”,而不是“五五开”。如果你不是LOL玩家,没关系,当我说“上火”、“金罐”这两个词,你能想到的下一个词应该更可能“加多宝”,而不是“可口可乐”。
N-gram正是基于这样的想法,它的第一个特点是某个词的出现依赖于其他若干个词,第二个特点是我们获得的信息越多,预测越准确。我想说,我们每个人的大脑中都有一个N-gram模型,而且是在不断完善和训练的。我们的见识与经历,都在丰富着我们的阅历,增强着我们的联想能力。
N-gram模型是一种语言模型(Language Model,LM),语言模型是一个基于概率的判别模型,它的输入是一句话(单词的顺序序列),输出是这句话的概率,即这些单词的联合概率(joint probability)。

N-gram本身也指一个由 N N N个单词组成的集合,各单词具有先后顺序,且不要求单词之间互不相同。常用的有 Bi-gram ( N = 2 N=2 N=2) 和 Tri-gram ( N = 3 N=3 N=3),一般已经够用了。例如在上面这句话里,我可以分解的 Bi-gram 和 Tri-gram :
Bi-gram : {I, love}, {love, deep}, {love, deep}, {deep, learning}
Tri-gram : {I, love, deep}, {love, deep, learning}
N-gram中的概率计算
假设我们有一个由 n n n个词组成的句子 S = ( w 1 , w 2 , ⋯ , w n ) S=(w_1,w_2,\cdots,w_n) S=(w1,w2,⋯,wn),如何衡量它的概率呢?让我们假设,每一个单词 w i w_i wi都要依赖于从第一个单词 w 1 w_1 w1到它之前一个单词 w i − 1 w_{i-1} wi−1的影响:
p ( S ) = p ( w 1 w 2 ⋯ w n ) = p ( w 1 ) p ( w 2 ∣ w 1 ) ⋯ p ( w n ∣ w n − 1 ⋯ w 2 w 1 ) p(S)=p(w_1w_2\cdots w_n)=p(w_1)p(w_2|w_1)\cdots p(w_n|w_{n-1}\cdots w_2w_1) p(S)=p(w1w2⋯wn)=p(w1)p(w2∣w1)⋯p(wn∣wn−1⋯w2w1)
是不是很简单?是的,不过这个衡量方法有两个缺陷:
- 参数空间过大,概率 p ( w n ∣ w n − 1 ⋯ w 2 w 1 ) p(w_n|w_{n-1}\cdots w_2w_1) p(wn∣wn−1⋯w2w1) 的参数有 O ( n ) O(n) O(n) 个。
- 数据稀疏严重,词同时出现的情况可能没有,组合阶数高时尤其明显。
为了解决第一个问题,我们引入马尔科夫假设(Markov Assumption):一个词的出现仅与它之前的若干个词有关。
p ( w 1 ⋯ w n ) = ∏ p ( w i ∣ w i − 1 ⋯ w 1 ) ≈ ∏ p ( w i ∣ w i − 1 ⋯ w i − N + 1 ) p(w_1\cdots w_n)=\prod p(w_i|w_{i-1}\cdots w_1)\approx \prod p(w_i|w_{i-1}\cdots w_{i-N+1}) p(w1⋯wn)=∏p(wi∣wi−1⋯w1)≈∏p(wi∣wi−1⋯wi−N+1)
- 如果一个词的出现仅依赖于它前面出现的一个词,那么我们就称之为 Bi-gram:
p ( S ) = p ( w 1 w 2 ⋯ w n ) = p ( w 1 ) p ( w 2 ∣ w 1 ) ⋯ p ( w n ∣ w n − 1 ) p(S)=p(w_1w_2\cdots w_n)=p(w_1)p(w_2|w_1)\cdots p(w_n|w_{n-1}) p(S)=p(w1w2⋯wn)=p(w1)p(w2∣w1)⋯p(wn∣wn−1) - 如果一个词的出现仅依赖于它前面出现的两个词,那么我们就称之为 Tri-gram:
p ( S ) = p ( w 1 w 2 ⋯ w n ) = p ( w 1 ) p ( w 2 ∣ w 1 ) ⋯ p ( w n ∣ w n − 1 w n − 2 ) p(S)=p(w_1w_2\cdots w_n)=p(w_1)p(w_2|w_1)\cdots p(w_n|w_{n-1}w_{n-2}) p(S)=p(w1w2⋯wn)=p(w1)p(w2∣w1)⋯p(wn∣wn−1wn−2)
N-gram的 N N N 可以取很高,然而现实中一般 bi-gram 和 tri-gram 就够用了。
那么,如何计算其中的每一项条件概率 p ( w n ∣ w n − 1 ⋯ w 2 w 1 ) p(w_n|w_{n-1}\cdots w_2w_1) p(wn∣wn−1⋯w2w1) 呢?答案是**极大似然估计(Maximum Likelihood Estimation,MLE)**,说人话就是数频数:
p ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) C ( w n − 1 ) p(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)}{C(w_{n-1})} p(wn∣wn−1)=C(wn−1)C(wn−1wn)
p ( w n ∣ w n − 1 w n − 2 ) = C ( w n − 2 w n − 1 w n ) C ( w n − 2 w n − 1 ) p(w_n|w_{n-1}w_{n-2})=\frac{C(w_{n-2}w_{n-1}w_n)}{C(w_{n-2}w_{n-1})} p(wn∣wn−1wn−2)=C(wn−2wn−1)C(wn−2wn−1wn)
p ( w n ∣ w n − 1 ⋯ w 2 w 1 ) = C ( w 1 w 2 ⋯ w n ) C ( w 1 w 2 ⋯ w n − 1 ) p(w_n|w_{n-1}\cdots w_2w_1)=\frac{C(w_1w_2\cdots w_n)}{C(w_1w_2\cdots w_{n-1})} p(wn∣wn−1⋯w2w1)=C(w1w2⋯wn−1)C(w1w2⋯wn)
具体地,以Bi-gram为例,我们有这样一个由三句话组成的语料库:

容易统计,“I”出现了3次,“I am”出现了2次,因此能计算概率:
p ( a m ∣ I ) = 2 3 p(am|I)=\frac{2}{3} p(am∣I)=32
同理,还能计算出如下概率:
p ( I ∣ < s > ) = 0.67 p ( S a m ∣ a m ) = 0.5 p ( < s > ∣ S a m ) = 0.5 p ( d o ∣ I ) = 0.33 p ( n o t ∣ d o ) = 1 p ( l i k e ∣ n o t ) = 1 \begin{matrix}p(I|)=0.67 & p(Sam | am)=0.5 & p(p(I∣<s>)=0.67p(do∣I)=0.33p(Sam∣am)=0.5p(not∣do)=1p(<s>∣Sam)=0.5p(like∣not)=1|Sam)=0.5 \\ p(do|I)=0.33 & p(not|do)=1 & p(like|not)=1\end{matrix}
另外再提供一个《Language Modeling with Ngrams》中的例子,Jurafsky et al., 1994 从加州一个餐厅的数据库中做了一些统计:



据统计, p ( I ∣ < s > ) = 0.25 p(I|)=0.25 p(I∣<s>)=0.25, p ( < s > ∣ f o o d ) = 0.68 p(|food)=0.68 p(<s>∣food)=0.68,于是:
p ( < s > I w a n t c h i n e s e f o o d < s > ) = 0.25 × 0.33 × 0.0065 × 0.52 × 0.68 = 1.896 × 1 0 − 4 p(I\ want\ chinese\ foodp(<s>I want chinese food<s>)=0.25×0.33×0.0065×0.52×0.68=1.896×10−4)\\=0.25\times 0.33\times 0.0065 \times 0.52 \times 0.68=1.896\times 10^{-4}
我们算出了“I want chinese food”这句话的概率,但有时候这句话会很长,那么概率(都是小于1的常数)的相乘很可能造成数据下溢(downflow),即很多个小于1的常数相乘会约等于0,此时可以使用log概率解决。
N-gram的用途
用途一:词性标注
N-gram可以实现词性标注。例如“爱”这个词,它既可以作为动词使用,也可以作为名词使用。不失一般性,假设我们需要匹配一句话中“爱”的词性。

我们可以将词性标注看成一个多分类问题,按照Bi-gram计算每一个词性概率:
p ( 词 性 i ∣ " 龙 龙 " 的 词 性 , " 爱 " ) = 前 面 是 “ 名 词 ” 的 “ 爱 ” 作 为 词 性 i 的 出 现 次 数 前 面 是 " 名 词 " 的 " 爱 " 的 出 现 次 数 p(词性_i|"龙龙"的词性, "爱")=\frac{前面是“名词”的“爱”作为词性_i 的出现次数}{前面是"名词"的"爱"的出现次数} p(词性i∣"龙龙"的词性,"爱")=前面是"名词"的"爱"的出现次数前面是“名词”的“爱”作为词性i的出现次数
选取概率更大的词性(比如动词)作为这句话中“爱”字的词性。
用途二:垃圾短信分类
文章开头提到的那个垃圾短信分类问题,我们可以用N-gram来解决。在朴素贝叶斯的基础上,稍微对条件概率做一点改动即可。
p ( 垃 圾 短 信 ∣ " 在 家 日 赚 百 万 " ) ∝ p ( 垃 圾 邮 件 ) p ( " 在 家 日 赚 百 万 " ∣ 垃 圾 短 信 ) p(垃圾短信|"在家日赚百万")\propto p(垃圾邮件)p("在家日赚百万"|垃圾短信) p(垃圾短信∣"在家日赚百万")∝p(垃圾邮件)p("在家日赚百万"∣垃圾短信)
条件概率不再是各词语之间独立:
p ( " 在 家 日 赚 百 万 " ∣ J ) = p ( " 在 " , " 家 " , " 日 " , " 赚 " , " 百 " , " 万 " ∣ J ) = p ( " 在 " ∣ J ) × p ( " 家 " ∣ " 在 " , J ) × p ( " 日 " ∣ " 家 " , J ) × p ( " 赚 " ∣ " 日 " , J ) × p ( " 百 " ∣ " 赚 " , J ) × p ( " 万 " ∣ " 百 " , J ) p("在家日赚百万"|J)=p("在","家","日","赚","百","万"|J)\\ =p("在"|J)\times p("家"|"在",J)\times p("日"|"家",J)\times\\p("赚"|"日",J)\times p("百"|"赚",J)\times p("万"|"百",J) p("在家日赚百万"∣J)=p("在","家","日","赚","百","万"∣J)=p("在"∣J)×p("家"∣"在",J)×p("日"∣"家",J)×p("赚"∣"日",J)×p("百"∣"赚",J)×p("万"∣"百",J)
垃圾短信分类问题可以总结为以下三个步骤:
- 步骤一:给短信的每个句子断句。
- 步骤二:用N-gram判断每个句子是否垃圾短信中的敏感句子。
- 步骤三:若敏感句子个数超过一定阈值,认为整个邮件是垃圾短信。
用途三:分词器
在NLP中,分词的效果很大程度上影响着模型的性能,因此分词甚至可以说是最重要的工程。用N-gram可以实现一个简单的分词器(Tokenizer)。同样地,将分词理解为多分类问题: X X X 表示有待分词的句子, Y i Y_i Yi 表示该句子的一个分词方案。
X = " 我 爱 深 度 学 习 " X="我爱深度学习" X="我爱深度学习"
Y 1 = { " 我 " , " 爱 深 " , " 度 学 习 " } Y 2 = { " 我 爱 " , " 深 " , " 度 学 " , " 习 " } Y 3 = { " 我 " , " 爱 " , " 深 度 学 习 " } Y_1=\{"我","爱深","度学习"\}\\ Y_2=\{"我爱","深","度学","习"\}\\ Y_3=\{"我","爱","深度学习"\} Y1={"我","爱深","度学习"}Y2={"我爱","深","度学","习"}Y3={"我","爱","深度学习"}
p ( Y 1 ) = p ( 我 ) p ( 爱 深 ∣ 我 ) p ( 度 学 习 ∣ 爱 深 ) p ( Y 2 ) = p ( 我 爱 ) p ( 深 ∣ 我 爱 ) p ( 度 学 ∣ 深 ) p ( 习 ∣ 度 学 ) p ( Y 3 ) = p ( 我 ) p ( 爱 ∣ 我 ) p ( 深 度 学 习 ∣ 爱 ) p(Y_1)=p(我)p(爱深|我)p(度学习|爱深)\\ p(Y_2)=p(我爱)p(深|我爱)p(度学|深)p(习|度学)\\ p(Y_3)=p(我)p(爱|我)p(深度学习|爱) p(Y1)=p(我)p(爱深∣我)p(度学习∣爱深)p(Y2)=p(我爱)p(深∣我爱)p(度学∣深)p(习∣度学)p(Y3)=p(我)p(爱∣我)p(深度学习∣爱)
三个概率中,“我爱”可能在语料库中比较常见,因此 p ( 爱 ∣ 我 ) p(爱|我) p(爱∣我)会比较大,然而“我爱深”这样的组合比较少见,于是 p ( 爱 深 ∣ 我 ) p(爱深|我) p(爱深∣我)和 p ( 深 ∣ 我 爱 ) p(深|我爱) p(深∣我爱)都比较小,导致 p ( Y 3 ) p(Y_3) p(Y3)比 p ( Y 1 ) p(Y_1) p(Y1)和 p ( Y 2 ) p(Y_2) p(Y2)都大,因此第三种分词方案最佳。
用途四:机器翻译和语音识别
机器翻译
同一句话,可能有多种翻译方式,它们的区别仅在于单词的组合顺序,这时候使用N-gram分别计算各种情况的概率,选最大的那个即可。
语音识别
同一种发音,可能被解析成不同的句子,然而其中有一种更符合语法规则。

N-gram中N的确定
为了确定 N N N的取值,《Language Modeling with Ngrams》使用了 Perplexity 这一指标,该指标越小表示一个语言模型的效果越好。文章使用了华尔街日报的数据库,该数据库的字典大小为19,979,训练集包含 38 million 个词,测试集包含 1.5 million 个词。针对不同的N-gram,计算各自的 Perplexity。
P P ( W ) = 1 P ( w 1 w 2 ⋯ w n ) n = ∏ i = 1 n 1 p ( w i ∣ w i − 1 ⋯ w 1 ) n PP(W)=\sqrt[n]{\frac{1}{P(w_1w_2\cdots w_n)}}=\sqrt[n]{\prod_{i=1}^n \frac{1}{p(w_i|w_{i-1}\cdots w_1)}} PP(W)=nP(w1w2⋯wn)1=ni=1∏np(wi∣wi−1⋯w1)1
结果显示,Tri-gram的Perplexity最小,因此它的效果是最好的。那么 N N N越大是否越好呢?

N-gram中的数据平滑方法
上面提到,N-gram的 N N N越大,模型 Perplexity 越小,表示模型效果越好。这在直观意义上是说得通的,毕竟依赖的词越多,我们获得的信息量越多,对未来的预测就越准确。然而,语言是有极强的创造性的(Creative),当 N N N变大时,更容易出现这样的状况:某些n-gram从未出现过,这就是稀疏问题。
n-gram最大的问题就是稀疏问题(Sparsity)。例如,在bi-gram中,若词库中有20k个词,那么两两组合( C 20 k 2 C_{20k}^2 C20k2)就有近2亿个组合。其中的很多组合在语料库中都没有出现,根据极大似然估计得到的组合概率将会是0,从而整个句子的概率就会为0。最后的结果是,我们的模型只能计算零星的几个句子的概率,而大部分的句子算得的概率是0,这显然是不合理的。
因此,我们要进行数据平滑(data Smoothing),数据平滑的目的有两个:一个是使所有的N-gram概率之和为1,使所有的n-gram概率都不为0。它的本质,是重新分配整个概率空间,使已经出现过的n-gram的概率降低,补充给未曾出现过的n-gram。
拉普拉斯平滑
Add-one
拉普拉斯平滑,即强制让所有的n-gram至少出现一次,只需要在分子和分母上分别做加法即可。这个方法的弊端是,大部分n-gram都是没有出现过的,很容易为他们分配过多的概率空间。
p ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) + 1 C ( w n − 1 ) + ∣ V ∣ p(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)+1}{C(w_{n-1})+|V|} p(wn∣wn−1)=C(wn−1)+∣V∣C(wn−1wn)+1
Add-K
在Add-one的基础上做了一点小改动,原本是加一,现在加上一个小于1的常数 K K K。但是缺点是这个常数仍然需要人工确定,对于不同的语料库 K K K可能不同。
p ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) + k C ( w n − 1 ) + k ∣ V ∣ p(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)+k}{C(w_{n-1})+k|V|} p(wn∣wn−1)=C(wn−1)+k∣V∣C(wn−1wn)+k
内插与回溯
内插
**内插法(Interpolation)**有点像滑动平均,它的核心思想是,既然高阶组合可能出现次数为0,那稍微低阶一点的组合总有不为0的。如下是一个三阶组合,假设 p ( w n ∣ w n − 1 w n − 2 ) = 0 p(w_n|w_{n-1}w_{n-2})=0 p(wn∣wn−1wn−2)=0,而 p ( w n ∣ w n − 1 ) > 0 p(w_n|w_{n-1})>0 p(wn∣wn−1)>0且 p ( w n ) > 0 p(w_n)>0 p(wn)>0,则加权平均后的概率不为0,从而达到平滑的效果。
p ^ ( w n ∣ w n − 1 w n − 2 ) = λ 3 p ( w n ∣ w n − 1 w n − 2 ) + λ 2 p ( w n ∣ w n − 1 ) + λ 1 p ( w n ) \hat{p}(w_n|w_{n-1}w_{n-2})=\lambda_3 p(w_n|w_{n-1}w_{n-2})+\lambda_2p(w_n|w_{n-1})+\lambda_1p(w_n) p^(wn∣wn−1wn−2)=λ3p(wn∣wn−1wn−2)+λ2p(wn∣wn−1)+λ1p(wn)
回溯
**回溯法(backoff)**与内插有点像,只是它会尽可能地用最高阶组合计算概率,当高阶组合不存在时,退而求其次找次低阶,直到找到非零组合为止。参考下式,这是一个递归运算。
p ( w n ∣ w n − 1 ⋯ w n − N + 1 ) = { p ∗ ( w n ∣ w n − 1 ⋯ w n − N + 1 ) C ( w n − 1 ⋯ w n − N + 1 ) > 0 α ( w n − 1 ⋯ w n − N + 1 ) p ( w n ∣ w n − 1 ⋯ w n − N + 2 ) o t h e r w i s e p(w_n|w_{n-1}\cdots w_{n-N+1})=\left \{ \begin{matrix} p^*(w_n|w_{n-1}\cdots w_{n-N+1}) & C(w_{n-1}\cdots w_{n-N+1})>0\\ \alpha(w_{n-1}\cdots w_{n-N+1})p(w_n|w_{n-1}\cdots w_{n-N+2}) & otherwise\end{matrix} \right . p(wn∣wn−1⋯wn−N+1)={p∗(wn∣wn−1⋯wn−N+1)α(wn−1⋯wn−N+1)p(wn∣wn−1⋯wn−N+2)C(wn−1⋯wn−N+1)>0otherwise
Absolute Discounting
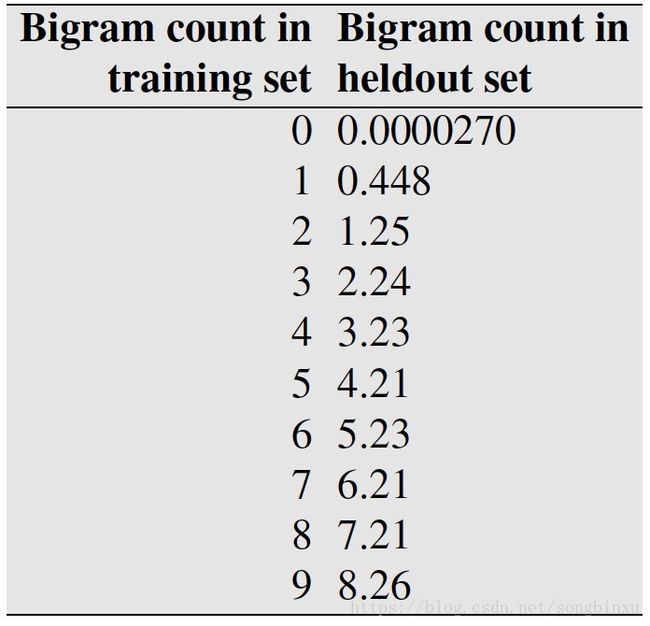
Church & Gale (1991) 取了个巧,他们在训练集里找到一些出现次数为 C = 4 C=4 C=4的bi-gram,然后在留出集(held-out)中统计它们的出现次数,平均下来发现约等于3.23。接着他们继续统计其他的 C C C,发现除了0和1外,基本上留出集bi-gram的出现次数等于训练集出现次数减去0.75。
因此,他们提出直接在分子上减去一个常数,然后在后面加上一项保证概率求和为1。此处 d = 0.75 d=0.75 d=0.75。
p ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) − d C ( w n − 1 ) + λ ( w n − 1 ) p ( w n ) p(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)-d}{C(w_{n-1})}+\lambda(w_{n-1})p(w_n) p(wn∣wn−1)=C(wn−1)C(wn−1wn)−d+λ(wn−1)p(wn)
Kneser-Ney Smoothing
考虑这样一个填空:
一个完形填空题,正常来说,我们可能会填入**“glasses”这个词,意思是“我不戴眼镜就看不到东西”。那么,考虑上面提到的内插模型:
λ 2 p ( w i ∣ w i − 1 ) + λ 1 p ( w i ) \lambda_2 p(w_i|w_{i-1})+\lambda_1 p(w_i) λ2p(wi∣wi−1)+λ1p(wi)
这个模型很可能会在这个空里填上“Kong”这个词,是不是觉得很奇怪?因为语料库里,“Hong Kong”** 这个词组是高频词汇,以至于 λ 1 p ( w i ) \lambda_1 p(w_i) λ1p(wi)这一项的概率会跟高,而**“glasses”是低频词,相应的概率较低,于是模型就填上了“Kong”**,在我们看来这显然是不合理的,但在模型看来却是合理的选择。
为了解决这个问题,Kneser and Ney (1995) , Chen and Goodman(1998) 提出,修改这个 p ( w i ) p(w_i) p(wi),具体来说,是要求它与“以 w i w_i wi为结尾的bi-gram的集合的势正相关的变量”,以表征 w i w_i wi这个单词作为一个新的接续的可能性(即作为其他单词的下一个词的可能性)。
以Bi-gram为例,实际上就是用下面这个 P c o n t i n u a t i o n P_{continuation} Pcontinuation代替原来的 p ( w ) p(w) p(w),所谓集合的势其实是要求集合中的元素互不相同后取集合的大小,其意义就是:语料库有多少种不同的以 w w w结尾的bi-gram。
P c o n t i n u a t i o n ( w ) ∝ ∣ { v : C ( v w ) > 0 } ∣ P_{continuation}(w)\propto |\left \{v:C(vw)>0\right\}| Pcontinuation(w)∝∣{v:C(vw)>0}∣
作为概率,需要进行归一化:
P c o n t i n u a t i o n ( w ) = ∣ { v : C ( v w ) > 0 } ∣ ∑ w ′ ∣ { v : C ( v w ′ ) > 0 } ∣ P_{continuation}(w)=\frac{|\left \{v:C(vw)>0\right\}|}{\sum_{w'}|\left\{v:C(vw')>0\right\}|} Pcontinuation(w)=∑w′∣{v:C(vw′)>0}∣∣{v:C(vw)>0}∣
那么,为什么这样改过之后就能有效解决 p ( K o n g ) p(Kong) p(Kong) 偏大的问题呢?根据 P c o n t i n u a t i o n P_{continuation} Pcontinuation 的定义,我们去统计语料库中以“Kong”结尾的bi-gram,然后发现只有“Hong Kong”一个,于是 P c o n t i n u a t i o n P_{continuation} Pcontinuation 就比较小了,而 “glasses”,可能有“sun glasses”,“reading glasses”等,相比“Hong Kong”这个专有名词肯定会更多。因此,问题得到解决。
Kneser-Ney Smoothing的本质是改进Unigram概率 p ( w ) p(w) p(w),像上文提到的其他用到这个概率的平滑方法,也可以代入这个概率,比如Absolute Discounting就变成:
p K N ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) − d C ( w n − 1 ) + λ ( w n − 1 ) P c o n t i n u a t i o n ( w n ) p_{KN}(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)-d}{C(w_{n-1})}+\lambda(w_{n-1})P_{continuation}(w_n) pKN(wn∣wn−1)=C(wn−1)C(wn−1wn)−d+λ(wn−1)Pcontinuation(wn)
N-gram对训练数据集的要求
关于N-gram的训练数据,如果你以为**“只要是英语就可以了”,那就大错特错了。文献《Language Modeling with Ngrams》**的作者做了个实验,分别用莎士比亚文学作品,以及华尔街日报作为训练集训练两个N-gram,他认为,两个数据集都是英语,那么用他们生成的文本应该也会有所重合。然而结果是,用两个语料库生成的文本没有任何重合性,即使在语法结构上也没有。
这告诉我们,N-gram的训练是很挑数据集的,你要训练一个问答系统,那就要用问答的语料库来训练,要训练一个金融分析系统,就要用类似于华尔街日报这样的语料库来训练。


N-gram的进化版:NNLM
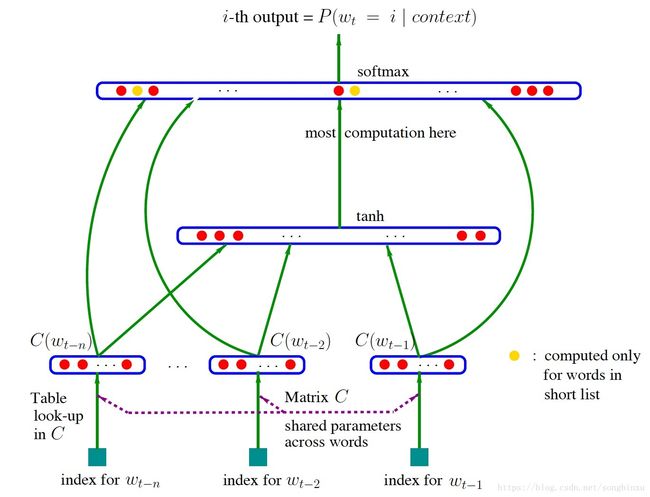
NNLM 即 Neural Network based Language Model,由Bengio在2003年提出,它是一个很简单的模型,由四层组成,输入层、嵌入层、隐层和输出层。模型接收的输入是长度为 n n n的词序列,输出是下一个词的类别。首先,输入是单词序列的index序列,例如单词 I 在字典(大小为 ∣ V ∣ |V| ∣V∣)中的index是10,单词 am 的 index 是23, Bengio 的 index 是65,则句子“I am Bengio”的index序列就是 10, 23, 65。嵌入层(Embedding)是一个大小为 ∣ V ∣ × K |V|\times K ∣V∣×K的矩阵,从中取出第10、23、65行向量拼成 3 × K 3\times K 3×K的矩阵就是Embedding层的输出了。隐层接受拼接后的Embedding层输出作为输入,以tanh为激活函数,最后送入带softmax的输出层,输出概率。
NNLM最大的缺点就是参数多,训练慢。另外,NNLM要求输入是定长 n n n,定长输入这一点本身就很不灵活,同时不能利用完整的历史信息。
NNLM的进化版:RNNLM
针对NNLM存在的问题,Mikolov在2010年提出了RNNLM,其结构实际上是用RNN代替NNLM里的隐层,这样做的好处包括减少模型参数、提高训练速度、接受任意长度输入、利用完整的历史信息。同时,RNN的引入意味着可以使用RNN的其他变体,像LSTM、BLSTM、GRU等等,从而在时间序列建模上进行更多更丰富的优化。
论文给的模型结构图不多,这里就不放出来了,有兴趣可以直接去读论文。另外,RNNLM有开源的工具包,自行编译后得到可执行文件,可在命令行中直接使用。
Word2Vec
Word2Vec解决的问题已经和上面讲到的N-gram、NNLM等不一样了,它要做的事情是:学习一个从高维稀疏离散向量到低维稠密连续向量的映射。该映射的特点是,近义词向量的欧氏距离比较小,词向量之间的加减法有实际物理意义。Word2Vec由两部分组成:CBoW和Skip-Gram。其中CBoW的结构很简单,在NNLM的基础上去掉隐层,Embedding层直接连接到Softmax,CBoW的输入是某个Word的上下文(例如前两个词和后两个词),Softmax的输出是关于当前词的某个概率,即CBoW是从上下文到当前词的某种映射或者预测。Skip-Gram则是反过来,从当前词预测上下文,至于为什么叫Skip-Gram这个名字,原因是在处理过程中会对词做采样。
Word2Vec这个内容比较丰富,这里只做一点概括性的描述,以后应该会再专门写一个博客。
参考资料
【博客】一周论文 | Word2Vec 作者Tomas Mikolov 的三篇代表作
【博客】word2vector:NPLM、CBOW、Skip-gram
【博客】大白话讲解word2vec到底在做些什么
【博客】Deep Learning in NLP (一)词向量和语言模型
【博客】word2vec前世今生
【博客】Hinton神经网络公开课编程题2–神经概率语言模型(NNLM)
【博客】神经网络语言模型(NNLM)
【博客】NLP系列(2)_用朴素贝叶斯进行文本分类(上)
【博客】NLP系列(5)_从朴素贝叶斯到N-gram语言模型
【博客】语言模型系列之N-Gram、NPLM及Word2vec
【博客】OpenNLP ngram n元语法模型(简介)
【博客】关于N-Gram模型(例子很好)
【博客】自然语言处理中的N-Gram模型详解
【博客】Deep Learning 读书笔记(十二):A Neural Probabilistic Language Model
【博客】Recurrent Neural Network Based Language Model(RNNLM)原理及BPTT数学推导
【博客】RNNLM的使用方法
【斯坦福课程】Speech and Language Processing
【NNLM论文】A Neural Probabilistic Language Models
【RNNLM论文】Statistical Language Models Based on Neural Networks
【开源】RNNLM Toolkit
