红黑树(删除)
本文地址:http://blog.csdn.net/spch2008/article/details/9338923
相对于红黑树插入操作,删除操作复杂的多。
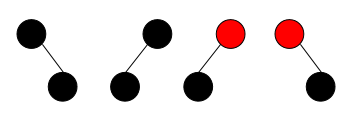
第一:先看最简单情况,即删除红色节点。删除红色节点,不影响红黑树平衡性质,如图:
只需要删除红色节点,不需要进行调整,因为不影响红黑树的性质。 黑色节点没有增多也没有减少。
注意:以下几种单支情况在平衡的红黑树中不可能出现。
因为上述的情况,红黑树处于不平衡状态。(破坏到null,黑色节点数目相同)
所以,平衡状态下红黑树要么单支黑-红,要么有两个子节点。第二:删除单支黑节点
此种情况被包含在“第三”中,详见“第三”分析
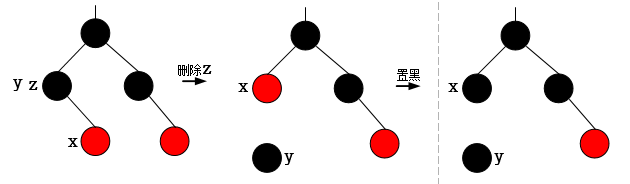
第三:若删除节点有左右两个儿子,即左右子树,需要按照二叉搜索树的删除规律,从右子树中找最小的替换删除节点(该节点至多有一个右子树,
无左子树),我们将该节点记为y, 将删除节点记为z,将y的右儿子记为x(可能为空)。
删除规则:用y替换z,交换y与z颜色,同时y = z,改变y的指向,让y指向最终删除节点。
为了便于理解,可以先这样假设:将y与z的数据交换,但颜色不交换,这样,实际相当于将删除转移到了y节点,而z处保持原先状态(处于平衡)。
此时可以完全不用了理会z节点,直接删除y节点即可。因为y最多只有一个右子树,无左子树,这便转移到了“第二”。
对于删除y节点,有几种考虑。
1. 若y为红色,则这种情况如上述”第一“所述,并不影响平衡性。(null视为黑色)
2. 若y为黑色,则删除y后,x替换了y的位置,这样x子树相对于兄弟节点w为根的子树少了一个黑节点,影响平衡,需要进行调整。
剩下的调整工作就是将x子树中找一合适红色节点,将其置黑,使得x子树与w子树达到平衡。
若x为红色,直接将x置为黑色,即可达到平衡;
若x为黑色,则分下列几种情况。
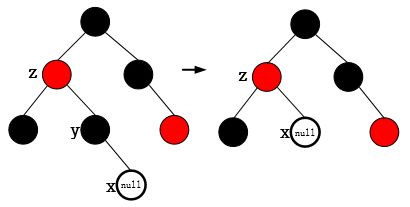
情况1:x的兄弟w为红色,则w的儿子必然全黑,w父亲p也为黑。
改变p与w的颜色,同时对p做一次左旋,这样就将情况1转变为情况2,3,4的一种。
情况2:x的兄弟w为黑色,x与w的父亲颜色可红可黑。
因为x子树相对于其兄弟w子树少一个黑色节点,可以将w置为红色,这样,x子树与w子树黑色节点一致,保持了平衡。
new x为x与w的父亲。new x相对于它的兄弟节点new w少一个黑色节点。如果new x为红色,则将new x置为黑,则整棵树平衡。否则,
情况2转换为情况1,3,4 情况2转变为情况1,2,3,4.
情况3:w为黑色,w左孩子红色,右孩子黑色。
交换w与左孩子的颜色,对w进行右旋。转换为情况4
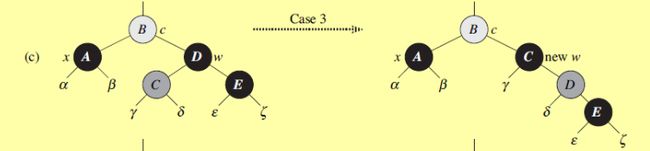
情况4:w为黑色,右孩子为红色。
交换w与父亲p颜色,同时对p做左旋。这样左边缺失的黑色就补回来了,同时,将w的右儿子置黑,这样左右都达到平衡。
个人认为这四种状况比较难以理解,总结了一下。情况2是最好理解的,减少右子树的一个黑色节点,使x与w平衡,将不平衡点上移至x与w的父亲。
进行下一轮迭代。情况1:如果w为红色,通过旋转,转成成情况1,2,3进行处理。而情况3转换为情况4进行处理。也就是说,情况4是最接近最终解
的情况。情况4:右儿子是红色节点,那么将缺失的黑色交给右儿子,通过旋转,达到平衡。
看一下STL的红黑树删除调整操作
if (y->color != __rb_tree_red) {
while (x != root && (x == 0 || x->color == __rb_tree_black))
if (x == x_parent->left) {
__rb_tree_node_base* w = x_parent->right;
//情况1
if (w->color == __rb_tree_red) {
w->color = __rb_tree_black;
x_parent->color = __rb_tree_red;
__rb_tree_rotate_left(x_parent, root);
w = x_parent->right;
}
//情况2
if ((w->left == 0 || w->left->color == __rb_tree_black) &&
(w->right == 0 || w->right->color == __rb_tree_black)) {
w->color = __rb_tree_red;
x = x_parent;
x_parent = x_parent->parent;
}
else
{
//情况3
if (w->right == 0 || w->right->color == __rb_tree_black) {
if (w->left) w->left->color = __rb_tree_black;
w->color = __rb_tree_red;
__rb_tree_rotate_right(w, root);
w = x_parent->right;
}
//情况4
w->color = x_parent->color;
x_parent->color = __rb_tree_black;
if (w->right) w->right->color = __rb_tree_black;
__rb_tree_rotate_left(x_parent, root);
break;
}
}
if (x) x->color = __rb_tree_black;
}