遗传算法解决TSP问题(Pyhton代码)

遗传算法的原理参考维基百科：https://zh.wikipedia.org/wiki/%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3%95

遗传算法流程图：

遗传算法的思想和流程都是很简单的，但是运用在具体应用时却会常常无从下手。如何编码解码，如何进行交叉是两个难点。

本文以用遗传算法解决旅行商问题(TSP)为例。

问题描述：现有34个城市，已知其坐标；从其中某一城市作为起点出发，途径其他的所有城市，然后回到起点，要求走过的距离最短。

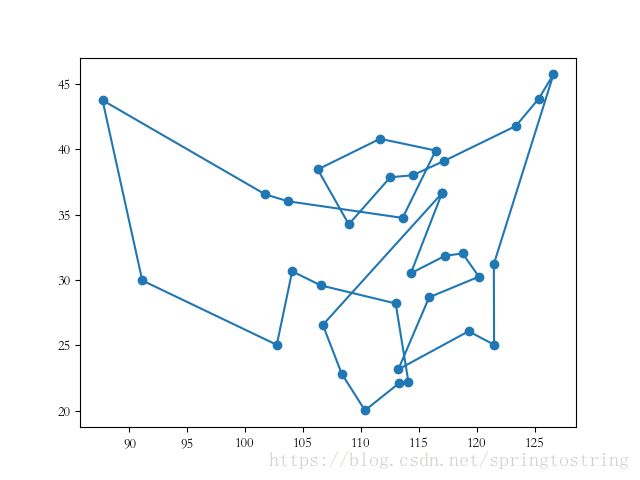
34个城市位置图如下所示：

重庆,106.54,29.59
拉萨,91.11,29.97
乌鲁木齐,87.68,43.77
银川,106.27,38.47
呼和浩特,111.65,40.82
南宁,108.33,22.84
哈尔滨,126.63,45.75
长春,125.35,43.88
沈阳,123.38,41.8
石家庄,114.48,38.03
太原,112.53,37.87
西宁,101.74,36.56
济南,117,36.65
郑州,113.6,34.76
南京,118.78,32.04
合肥,117.27,31.86
杭州,120.19,30.26
福州,119.3,26.08
南昌,115.89,28.68
长沙,113,28.21
武汉,114.31,30.52
广州,113.23,23.16
台北,121.5,25.05
海口,110.35,20.02
兰州,103.73,36.03
西安,108.95,34.27
成都,104.06,30.67
贵阳,106.71,26.57
昆明,102.73,25.04
香港,114.1,22.2
澳门,113.33,22.13

采用遗传算法解决此问题：

为了简化说明，对城市进行编号0，1，2，3……33

由于起点是任意的，不影响结果的，所以取起点为城市15

参数设计：种群规模count=3000，染色体长度length=33，进化次数itter_time=300

编码策略采用十进制：直接用城市的编号进行编码，染色体{1，2，……33}表示路径为15-1-2-……-33。

初始化种群：为了加快程序的运行速度，在初始种群的选取中要选取一些较优秀的个体。我们先利用经典的近似算法—改良圈算法求得一个较好的初始种群。算法思想是随机生成一个染色体，比如{1，2，……33}，任意交换两城市顺序位置，如果总距离减小，则更新改变染色体，如此重复，直至不能再做修改。

对应代码：

#改良
def improve(x):
    i=0
    distance=get_total_distance(x)
    while i

交叉策略：交叉策略是本问题的难点，如果直接采用点交叉那么得到的子代染色体会出现城市重复和城市遗漏的问题。所以采用次序交叉法。次序杂交算法首先 随机地在双亲中选择两个杂交点，再交换杂交段，其他 位置根据双亲城市的相对位置确定。例如：A1[10]={0， 8，5，4，7，3，1，6，9，2}，A2[10]={1，5，4，6，9，0，3，2，8，7}， 随机杂交点为 4，7。 首先交换杂交段: B1[10]={&，&，&，&|9，0，3，2|&，&} B2[10]={&，&， &，&|7，3，1，6|&，&}， 从 A1 的第二个杂交点开始 9— 2—0—8—5—4—7—3—1—6，去除杂交段中的元素得 8—5—4—7—1—6， 依次从第二个杂交点开始填入得 B1[10]={4，7，1，6，9，0，3，2，8，5}，同理得 B2[10]={4，9， 0，2，7，3，1，6，8，5}。

对应代码：

#交叉繁殖
def crossover(parents):
    #生成子代的个数,以此保证种群稳定
    target_count=count-len(parents)
    #孩子列表
    children=[]
    while len(children)

变异：变异也是实现群体多样性的一种手段，同时也是全局寻优的保证。具体设计如下， 按照给定的变异率，对选定变异的个体，随机地取三个整数，满足 1

对应代码：

#变异
def mutation(children):
    for i in range(len(children)):
        if random.random() < mutation_rate:
            child=children[i]
            u=random.randint(1,len(child)-4)
            v = random.randint(u+1, len(child)-3)
            w= random.randint(v+1, len(child)-2)
            child=children[i]
            child=child[0:u]+child[v:w]+child[u:v]+child[w:]

全部代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import math
import random
matplotlib.rcParams['font.family']= 'STSong'

#载入数据
city_name=[]
city_condition=[]
with open('data.txt','r') as f:
    lines=f.readlines()
    for line in lines:
        line=line.split('\n')[0]
        line=line.split(',')
        city_name.append(line[0])
        city_condition.append([float(line[1]),float(line[2])])
city_condition=np.array(city_condition)

#展示地图
# plt.scatter(city_condition[:,0],city_condition[:,1])
# plt.show()

#距离矩阵
city_count=len(city_name)
Distance=np.zeros([city_count,city_count])
for i in range(city_count):
    for j in range(city_count):
        Distance[i][j]=math.sqrt((city_condition[i][0]-city_condition[j][0])**2+(city_condition[i][1]-city_condition[j][1])**2)


#种群数
count=300
#改良次数
improve_count=10000
#进化次数
itter_time=3000

#设置强者的定义概率，即种群前30%为强者
retain_rate=0.3

#设置弱者的存活概率
random_select_rate=0.5

#变异率
mutation_rate=0.1

#设置起点
origin=15
index=[i for i in range(city_count)]
index.remove(15)


# def get_path(x):
#     graded = [[x[i], index[i]] for i in range(len(x))]
#     graded_index = [t[1] for t in sorted(graded)]
#     return graded_index
#总距离
def get_total_distance(x):
    distance=0
    distance+=Distance[origin][x[0]]
    for i in range(len(x)):
        if i==len(x)-1:
            distance += Distance[origin][x[i]]
        else:
            distance += Distance[x[i]][x[i+1]]
    return distance

#改良
def improve(x):
    i=0
    distance=get_total_distance(x)
    while i

最终结果图如下：

可以增加代数，增加变异率，得到更加好的结果。

PS:有好几个人找我要数据文件，之前比较忙，都没有及时回复。如果数据文件运行有问题的话，再最后一行加个回车就可以解决问题了。