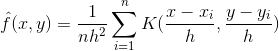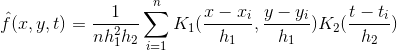核密度

最近涉及到建模分析的时候，去研究了一下核密度函数模型，看了一些论文和博客，感觉还是有一点懵，最后又看了看知乎，决定自己写一篇关于核密度的东西。

1.核密度简介

简单地讲，核密度估计是对直方图的一个自然拓展

https://blog.csdn.net/unixtch/article/details/78556499

这个链接是对核密度介绍比较详细的一篇文章，可以先去看一下，主要讲了从直方图到核密度估计，再到核函数和窗宽的估计。

2.核密度估计

这种估计的意思是，你给出模型一个解释变量，可以得到模型估计出来的被解释变量。如给出 ，模型用知道的有关x，y的全部知识，告诉你对 的估计值。以 点为中心，找了窗宽范围内的所有点（无视外面的点），以距离 远近为权重，给范围内每一个x所对应的y点做一个加权求和取平均。而权重设置和加和过程涉及到一定的规则，这个规则就是核函数。

3.核函数

核函数K（kernel function）就是指K(x, y) = ，其中x和y是n维的输入值，f(·) 是从n维到m维的映射（通常，m>>n）。是x和y的内积（inner product）(也称点积（dot product）)。

（1）举例：
令 x = (x1, x2, x3, x4); y = (y1, y2, y3, y4);
令 f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4); f(y)亦然；
令核函数 K(x, y) = ()^2.
接下来，让我们带几个简单的数字进去看看是个什么效果：x = (1, 2, 3, 4); y = (5, 6, 7, 8). 那么：
f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16) ;
f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64) ;
= 25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024
= 4900. 
如果我们用核函数呢？
K(x, y) = (5+12+21+32)^2 = 70^2 = 4900.

（2）核密度估计中的核函数K(x)

在核密度估计中，核函数一般选取标准正态概率密度函数ϕ(x)

       

4.密度函数

     

其中n为样本总数，x为当前输入变量，h为窗宽。

对于数据较多的情况，可能就要用到多维核密度函数模型了，在论文中看到过一些，具体的如下：

二维：

三维：

对于多维情况，如没有特殊的关系等，可以考虑直接将多个一维的相乘。

 

参考：

https://www.researchgate.net/publication/223677041_Visualising_space_and_time_in_crime_patterns_A_comparison_of_methods

https://www.zhihu.com/question/27301358