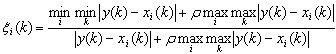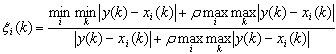灰色关联分析(GRA)的理论及应用（matlab和python）

---

什么是灰色关联分析

灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。

通常可以运用此方法来分析各个因素对于结果的影响程度，也可以运用此方法解决随时间变化的综合评价类问题，其核心是按照一定规则确立随时间变化的母序列，把各个评估对象随时间的变化作为子序列，求各个子序列与母序列的相关程度，依照相关性大小得出结论。

---

灰色关联分析的步骤

灰色关联分析的具体计算步骤如下：

第一步：确定分析数列。

确定反映系统行为特征的参考数列和影响系统行为的比较数列。反映系统行为特征的数据序列，称为参考数列。影响系统行为的因素组成的数据序列，称比较数列。

（1）参考数列（又称母序列）为$Y=Y(k)|k=1,2...n$；

（2）比较数列（又称子序列）为$X_i=X_i(k)|k=1,2...n,i=1,2...m$。

第二步，变量的无量纲化

由于系统中各因素列中的数据可能因量纲不同，不便于比较或在比较时难以得到正确的结论。因此在进行灰色关联度分析时，一般都要进行数据的无量纲化处理。主要有一下两种方法
　　
（1）初值化处理：$x_i(k)=\frac{x_i(k)}{x_i(1)},k=1,2...n;i=0,1,2...m$

（2）均值化处理：$x_i(k)=\frac{x_i(k)}{\overline{x_i}},k=1,2...n;i=0,1,2...m$

其中$k$ 对应时间段，$i$ 对应比较数列中的一行（即一个特征）

第三步，计算关联系数

记${△}_i(k)=|y(k)-x_i(k)|$，则
　　

$\rho \in (0,\infty )$，称为分辨系数。ρ越小，分辨力越大，一般ρ的取值区间为$(0,1)$,具体取值可视情况而定。当$\rho \le 0.5463$时，分辨力最好，通常取$\rho =0.5$。

第四步，计算关联度

因为关联系数是比较数列与参考数列在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。因此有必要将各个时刻（即曲线中的各点）的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，关联度$ri$公式如下：

$r_i=\frac{1}{n}{\sum }_{k=1}^n{\xi }_i(k),k=1,2,\Lambda ,n$

第五步，关联度排序

关联度按大小排序，如果$r1<r2$，则参考数列$y$与比较数列$x2$更相似。

在算出$Xi(k)$序列与$Y(k)$序列的关联系数后，计算各类关联系数的平均值，平均值$ri$就称为$Y(k)$与$Xi(k)$的关联度。

---

灰色关联分析的实例

下表为某地区国内生产总值的统计数据（以百万元计），问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大。

年份	国内生产总值	第一产业	第二产业	第三产业
2000	1988	386	839	763
2001	2061	408	846	808
2002	2335	422	960	953
2003	2750	482	1258	1010
2004	3356	511	1577	1268
2005	3806	561	1893	1352

步骤1：确立母序列

在此需要分别将三种产业与国内生产总值比较计算其关联程度，故母序列为国内生产总值。若是解决综合评价问题时则母序列可能需要自己生成，通常选定每个指标或时间段中所有子序列中的最佳值组成的新序列为母序列。

步骤2：无量纲化处理

在此采用均值化法，即将各个序列每年的统计值与整条序列的均值作比值，可以得到如下结果：

年份	国内生产总值	第一产业	第二产业	第三产业
2000	0.7320	0.8361	0.6828	0.7439
2001	0.7588	0.8838	0.6885	0.7878
2002	0.8597	0.9141	0.7812	0.9292
2003	1.0125	1.0440	1.0237	0.9847
2004	1.2356	1.1069	1.2833	1.2363
2005	1.4013	1.2152	1.5405	1.3182

步骤3：计算每个子序列中各项参数与母序列对应参数的关联系数

其中${\xi }_i(k)$表示第$i$个子序列的第$k$个参数与母序列（即0序列）的第$k$个参数的关联系数，$\rho\ $为分辨系数取值范围在$[0,1]$，其取值越小求得的关联系数之间的差异性越显著，在此取为0.5进行计算可得到如下结果：

年份	S01（t）	S02（t）	S03（t）
2000	0.4755	0.6591	0.8933
2001	0.4299	0.5739	0.7681
2002	0.6358	0.5465	0.5767
2003	0.7527	0.8993	0.7758
2004	0.4228	0.6661	1.0000
2005	0.3358	0.4037	0.5322

步骤4：计算关联度

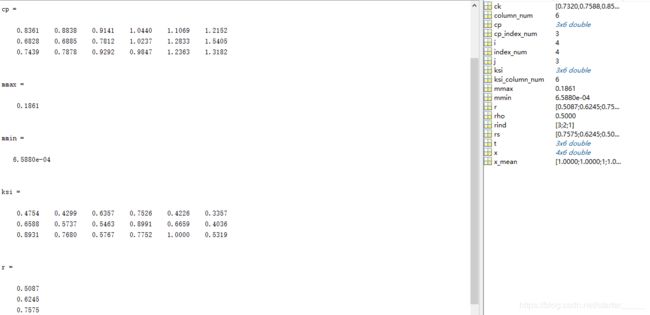
用公式$r_i=\frac{1}{n}{\sum }_{k=1}^n{\xi }_i(k),k=1,2,\Lambda ,n$， 可以得到$r1=0.5088，r2=0.6248，r3=0.7577$，通过比较三个子序列与母序列的关联度可以得出结论：该地区在2000年到2005年期间的国内生产总值受到第三产业的影响最大。

---

灰色关联分析matlab的实现

clc;
close;
clear all;
x=xlsread('data.xlsx');
x=x(:,2:end)';
column_num=size(x,2);
index_num=size(x,1);

% 1、数据均值化处理
x_mean=mean(x,2);
for i = 1:index_num
    x(i,:) = x(i,:)/x_mean(i,1);
end
% 2、提取参考队列和比较队列
ck=x(1,:)
cp=x(2:end,:)
cp_index_num=size(cp,1);

%比较队列与参考队列相减
for j = 1:cp_index_num
    t(j,:)=cp(j,:)-ck;
end
%求最大差和最小差
mmax=max(max(abs(t)))
mmin=min(min(abs(t)))
rho=0.5;
%3、求关联系数
ksi=((mmin+rho*mmax)./(abs(t)+rho*mmax))

%4、求关联度
ksi_column_num=size(ksi,2);
r=sum(ksi,2)/ksi_column_num;

%5、关联度排序，得到结果r3>r2>r1
[rs,rind]=sort(r,'descend');

运行结果：

---

灰色关联分析python的实现

import pandas as pd
x=pd.read_excel('data.xlsx')
x=x.iloc[:,1:].T

# 1、数据均值化处理
x_mean=x.mean(axis=1)
for i in range(x.index.size):
    x.iloc[i,:] = x.iloc[i,:]/x_mean[i]

# 2、提取参考队列和比较队列
ck=x.iloc[0,:]
cp=x.iloc[1:,:]

# 比较队列与参考队列相减
t=pd.DataFrame()
for j in range(cp.index.size):
    temp=pd.Series(cp.iloc[j,:]-ck)
    t=t.append(temp,ignore_index=True)

#求最大差和最小差
mmax=t.abs().max().max()
mmin=t.abs().min().min()
rho=0.5
#3、求关联系数
ksi=((mmin+rho*mmax)/(abs(t)+rho*mmax))


#4、求关联度
r=ksi.sum(axis=1)/ksi.columns.size

#5、关联度排序，得到结果r3>r2>r1
result=r.sort_values(ascending=False)

---