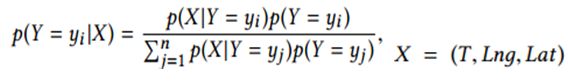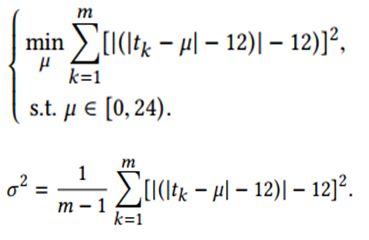数据挖掘顶会 KDD 2017 已经开幕,国内有众多来自产业界的论文被 KDD 2017 接收。本文是对滴滴 KDD 2017 论文的介绍。基于滴滴的应用场景,他们提出了一种基于组合优化的出租车分单模型。
掏出手机,轻点几下,键入目的地、发单,几分钟后,一位出租车司机准时出现在楼下等你。这一操作已经被数亿用户所熟悉。
看似简单的背后其实是一个多层次处理问题的过程。期间,有一系列复杂的智能算法模型在默默地为你提供服务,快速地进行超大规模地计算。
实际上,相比于在搜索引擎中找到一个你想要的网页,在茫茫车潮中匹配到一辆载你去目的地的车辆会更加复杂。毕竟,网页可以持续呈现一整天,甚至半个月;但车辆是高速移动的,乘客和司机的相对位置一直在实时变动。匹配的过程和方式也极其重要,在一个既定区域,乘客有很多,车辆也有很多,系统需要全局考虑区域内的需求、供给,以毫秒级的速度进行计算,实时地进行最合理的分单,最大化用户的出行效率和出行体验。
在滴滴出行,从乘客发出一个出租车订单,到订单被播报给周围的出租车司机,再到成功被司机应答,所需的时间被压缩到极短。这背后的最大功臣,就是基于组合优化的滴滴出租车分单模型。这一模型投入使用后,滴滴出租车的打车成功率较之前进一步提升。
而为了进一步提高用户叫车时的体验,滴滴还开发出一个目的地预测模型,能在用户打开软件时,2 毫秒为用户推荐出他最可能前往的地点。目前这一功能的预测准确率已经超过 90%。
相关论文《A Taxi Order DispatchModel based On Combinatorial Optimization》也被国际数据挖掘顶级会议 KDD 2017 收录。
以下是对该论文的中文概述:
论文:http://www.kdd.org/kdd2017/papers/view/a-taxi-order-dispatch-model-based-on-combinatorial-optimization
1. 我们的工作:分单时优化整体成交率
早期,出租车打车软件的订单分配主要聚焦在每个订单与每个出租车司机的相关性算法上。当一个乘客发起一单需求,系统会尽量匹配调度最近距离的司机,力图让接驾时间最短。然而此时往往会忽略到这些司机是否更适合其他订单。
此前业界曾提出过一个基于多代理体系结构的新模型 NTuCab,它的目的是最小化乘客的等待时间和接驾距离。这一模型会将每个代理视为一个计算单元,它会同时计算处理 N 个订单和司机的匹配,但一个订单只会匹配一个出租车司机。如果一个出租车司机拒绝该订单,系统才会转发给下一司机。
然而这些方法的调度时间往往偏长,成功率较低。对此,滴滴出行提出了新的组合优化方法。在这个模型中,一个订单会播报给几个出租车司机,当多个出租车司机收到相同的订单时,最先抢单的人会获得订单。如果订单未被应答,则进入下一轮播单,直到它被出租车司机应答或被乘客取消。而模型的目标则是最大化订单成交率,从而确保司机和乘客的出行体验。实验数据也显示,这一模型下打车的全局成功率比同类模型高出了 4%。
我们工作一个主要的改进是使用「整体」的概念,即会整体考虑当前时刻所有待分配司机和订单群体的多对多的匹配问题。以成交率为优化目标,通过整体分配司机与乘客,提升乘客订单的整体成交率。
模型的数学形式即:
其中,maxE 为整个模型的优化目标,即成交率;g(a)≤ 0 为模型必须要满足的约束条件,在这里可能是一些业务规则,比如一个司机同一时刻只能分配一个订单等;a 为模型的解,即如何对整体的订单和整体的司机进行分配。
假设当前有 n 个待分配订单,m 个待分配出租车司机,那么整体的待分配订单与待分配司机的匹配结果可以定义为一个 m*n 的矩阵 A_m*n,其元素 a_ij 的含义如下:
其中,下标 i 代表订单,j 代表司机。考虑到每个出租车司机同一时刻只能播送 1 个订单,那么对每个司机,也就是每个 j 而言,其至多只能播送 n 个订单中的一个,表现在 A_m*n 矩阵中,就是对每个 j 的一列,至多只能出现 1 个「1」,其余必须全部为「0」。即:
2. Logistics regression 模型计算司机接受概率
虽然对模型的目标和求解进行了定义,但这其中,还存在一个关键因素,我们需要考虑司机对订单的接受意愿。司机接受订单的概率往往取决于诸多因素,如订单的价值、接驾距离、方向夹角、行驶方向等。这些信息可以编码成特征向量 x_ij。
我们用 p_ij 表示司机 d_j 对订单 o_i 的接受概率,关于这个概率的计算,我们借鉴了计算广告学中 CTR 预估的方法,采用 logistics regression 模型来进行计算。
我们采用日志中的数据对 logistics regression 进行训练,以司机是否接受为 y,其余特征为向量 x,训练得到 sigmod 函数  中的权重向量 w。
中的权重向量 w。
将司机对订单的接受概率与模型关联起来,第 i 个订单的成交概率即为:
这样整个组合优化模型即为:
我们在北京进行了严格的 AB 测试,将我们的模型与另外两种行业普遍运用的模型进行了比较,把成交率、平均接驾时长、订单应答时长、取消率等业务关键指标作为核心评价指标。实验结果显示,我们的模型有更好的表现效果,订单整体的成交率提高了 4%。
3. 预测目的地:循环正态分布下的概率计算
在寒风凛冽的冬天,让用户哆哆嗦嗦地输入目的地,这个体验并不算好。如果能够在用户发出订单前,率先为用户推荐他最可能前往的地点,往往可以大幅减少他自行操作软件时间。
基于滴滴平台海量的历史数据,我们发现,人们的出行往往存在一定的规律,用户往往倾向在类似的时间到达相同的目的地;而对订单的位置进行分析,也有助于精准推荐用户的实时目的地。
基于这一观察,我们使用了贝叶斯公式建立用户目标的概率分布模型:
其中,T 代表当前时间,D 表示日期,(lat,lng) 表示经纬度,{y1,y2,…,yi,…,yn} 表示目的地的可能性,X 表示出发地的时间和经纬度。那么剩下的问题是估计出发时间和地点 (经度和纬度) 的概率分布:
![]()
而历史数据分析显示,用户目的地的出发时刻的频率直方图往往呈现如下正态分布,于是我们采用正态分布对出发时刻 T 的条件分布进行估计。但如何估计这个分布的期望μ和标准差σ,这就成为一个需要思考的问题。
考虑到时间和经纬度的分布具有周期循环性,均值和方差不能用传统方法来估计。因此我们使用了循环正态分布,建成一个优化模型,通过求解,得到了期望的平均值和方差。
这样整个算法的流程变为:首先根据用户的历史订单,依次计算每个目的地对应的发单时刻的期望和方差;然后根据当前时间计算每个目的地概率的中间数据;第三步用贝叶斯框架计算每个目的地的概率;最后确定阈值,满足阈值的就是我们要的计算结果:
Step1:根据用户订单历史,估计每个目的地的发单时刻集合的μ和σ;
Step2:根据当前时间,计算每个目的地的 P(T|X_i) 和频率 P(X_i);
Setp3:计算每个目的地的概率
Step4:确定支持度阈值 s 和概率阈值 p,对满足阈值的予以首屏展示。
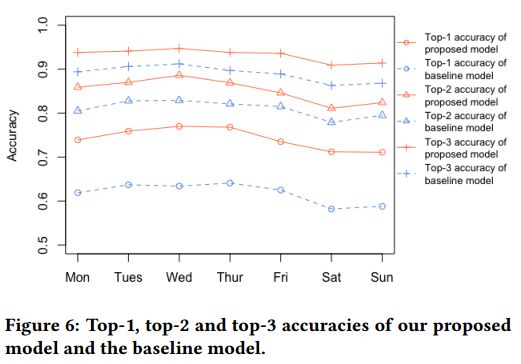
实验数据显示,我们的这一预测模型明显优于基线模型,这一模型下的预估准确率达 93%,较基线模型高出了 4 个百分点。