词向量模型（word2vec）总结笔记

引言

自从Mikolov在他2013年的论文“Efficient Estimation of Word Representation in Vector Space”提出词向量的概念后，NLP领域仿佛一下子进入了embedding的世界，Sentence2Vec、Doc2Vec、Everything2Vec。词向量基于语言模型的假设——“一个词的含义可以由它的上下文推断得出“，提出了词的Distributed Representation表示方法。相较于传统NLP的高维、稀疏的表示法(One-hot Representation)，Word2Vec训练出的词向量是低维、稠密的。

在上一篇文章里，我们用onehot将词转换成向量的形式，如下所示：

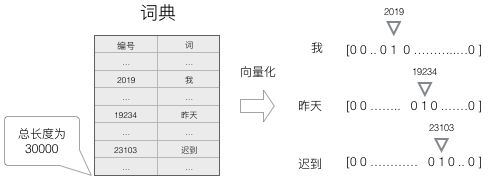
假设有二、三、四元词进行onehot，我们可能得到的特征为：

feature1=[01,10]
feature2=[001,010,100]
feature3=[0001,0010,0100,1000]

而如果依照上面的特征，我们发现会出现正交的情况，那么根据余弦相似度的关系，$\mathbf{a}\cdot \mathbf{b}=\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos \theta$，这将导致任何一对词的余弦相似度为0，而它得到的特征也将是离散稀疏的。

word2vec介绍

关于word2vec，我们知道的CBOW(Continuous Bag-of-Words Model)和Skip-gram (Continuous Skip-gram Model)，都是它的两种训练模式。而负采样（Negative Sample）和层次softmax（Hierarchical Softmax）则是两种加速训练的方法。

跳字模型（skip-gram）

在跳字模型中，词典索引集$\mathcal{V}=\{0,1,\dots ,|\mathcal{V}|-1\}$。假设给定一个长度为$T$的文本序列，设时间步$t$的词为$w^{(t)}$。假设给定中心词的情况下背景词的生成相互独立，当背景窗口大小为$m$时，跳字模型的似然函数即给定任一中心词生成所有背景词的概率

$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(w^{(t+j)}\mid w^{(t)}),$$

m为窗口大小，比如说m=2也就是滑窗大小为5，T为文本序列的总长度，上式也为给定中心词的极大似然估值。而在之前的softmax章节中提到过，若要使得整个联合概率最大化，这个联合概率最大化就等价于最小化这个损失函数，那么上式就能等价于：

$$-\frac{1}{T}\sum _{t=1}^T\sum _{-m\le j\le m,j\ne 0}\text{log}P(w^{(t+j)}\mid w^{(t)})$$

我们可以用$v$和$u$分别代表中心词和背景词的向量。换言之,对于词典中一个索引为$i$的词，它在作为中心词和背景词时的向量表示分别是$v_i$和$u_i$。而词典中所有词的这两种向量正是跳字模型所要学习的模型参数。为了将模型参数植入损失函数，我们需要使用模型参数表达损失函数中的中心词生成背景词的概率。设中心词 $w_c$ 在词典中索引为 ，背景词 $w_o$ 在词典中索引为 ，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}$$

当序列长度T较大时，我们通常随机采样一个较小的子序列来计算损失函数并使用随机梯度下降优化该损失函数。根据定义：

$$\frac{\partial \log \mathbb{P}\left(w_o|w_c\right)}{\partial v_c}=u_o-\sum _{j\in \mathcal{V}}\frac{\exp \left(u_j^{\top }{v}_c\right)}{{\sum }_{i\in \mathcal{V}}\exp \left(u_i^{\top }{v}_c\right)}{u}_j$$

通过微分，可以得到：

$$\begin{array}{rl}\frac{\partial \text{log}P(w_o\mid w_c)}{\partial {\mathbf{v}}_c}& ={\mathbf{u}}_o-\frac{{\sum }_{j\in \mathcal{V}}\exp ({\mathbf{u}}_j^{\top }{\mathbf{v}}_c){\mathbf{u}}_j}{{\sum }_{i\in \mathcal{V}}\exp ({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}\left(\frac{\text{exp}({\mathbf{u}}_j^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\right){\mathbf{u}}_j\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}P(w_j\mid w_c){\mathbf{u}}_j.\end{array}$$

上式即为我们求得的词向量的梯度，它的计算需要词典中所有词以$w_c$为中心词的条件概率。

连续词袋模型（continuous bag of words，CBOW）

同样，连续词袋模型和词袋模型基本一致，与跳字模型最大的不同在于，连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。举个例子，给定背景词“the”“man”“his”“son”生成中心词“loves”的条件概率，也就是：

$$P(‘‘loves"\mid ‘‘the",‘‘man",‘‘his",‘‘son")$$

给定一个长度为$T$的文本序列，设时间步$t$的词为$w_t$ ，背景窗口大小为$m$。连续词袋模型的似然函数是由背景词生成任一中心词的概率：

$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})$$

连续词袋模型的最大似然估计等价于最小化损失函数：

$$-\sum _{t=1}^T\text{log}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})$$

那么再对上式做softmax运算就可以得到：

$$\mathbb{P}\left(w_c|w_{o_1},\dots ,w_{o_{2m}}\right)=\frac{\exp \left[{\mathbf{u}}_c^{\top }\left({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2n}}\right)/(2m)\right]}{{\sum }_{i\in \mathcal{V}}\exp \left[{\mathbf{u}}_i^{\top }\left({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}}\right)/(2m)\right]}$$

同样，当序列长度$T$较大时，我们通常随机采样一个较小的子序列来计算损失函数并使用随机梯度下降优化损失函数：

$$\frac{\partial \log \mathbb{P}(w_c|w_{o_1},...,w_{o_2)}}{\partial v_{o_i}}=\frac{1}{2m}\left(u_c-\sum _{j\in \mathcal{V}}\frac{\exp \left(u_j^{\top }{v}_c\right)}{{\sum }_{i\in V}\exp \left(u_i^{\top }{v}_c\right)}{u}_j\right)$$

负采样（Negative sampling）