统计学习方法 | k近邻法

01 起

K近邻法（KNN）是一种基本的分类与回归方法

分类这种需求，渗透到我们生活的方方面面：

• 根据学生德智体美成绩，将学生分为几类
• 根据一个县城的GDP、人口密度等数据，将全国的县城分为多个类别
• 根据客户的信用、收入、生活习惯将客户分为多个类别
• ……

分类算法可以帮助我们完成这些繁琐的操作，并根据我们的要求不断修正分类结果。

分类算法其实蛮多的，这里顺着书本顺序，详细讲解KNN算法，再与K-Means、K-Means++算法进行简单对比。

---

02 KNN算法

k近邻法是这样一个过程：

给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类（多数表决argmax），就把该输入实例分为这个类。

过程其实很好理解，描述成可量化的算法，就是这样的：

KNN是一种懒惰算法，平时不好好学习，考试（对测试样本分类）时才临阵磨枪（临时去找k个近邻）。

懒惰的后果：构造模型很简单，但在对测试样本分类的开销大，因为要扫描全部训练样本并计算距离。

理解算法后，我们来看看k近邻法的优缺点：

优点：易于实现，无需估计参数，无需训练，支持增量学习，能对超多边形的复杂决策空间建模

缺点：计算量较大，分析速度慢（因为要扫描全部训练样本并计算距离）

03 KNN vs K-Means vs K-Means++

开头我们说到，分类算法很多，KNN只是其中一种，下面我们将KNN算法与K-Means、K-Means++进行对比，便于我们更好地理解算法。

KNN
给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类（多数表决argmax），就把该输入实例分为这个类。

K-Means
不断地聚类<–>划分过程
（1）对于一组数据集，任意选取k个点作为质心，将数据集中的点归为离其最近的质心一类，此时数据集被划分为k个类；
（2）对这k个类，重新寻找各类的质心；
（3）根据新产生的质心，按照（1）继续聚类，然后再根据聚类重新计算各类质心，直到质心不再改变，分类完成。

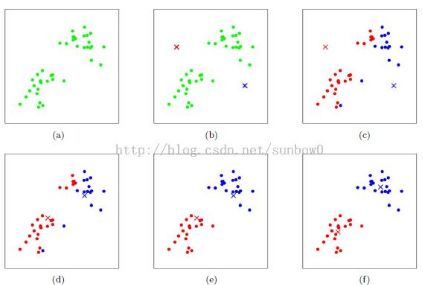
下面的图可以很直观地展示整个分类过程

K-Means++
与K-Means算法相同，除了第一步初始质心的选择：选择初始质心时并不是随机选择，而是选择尽量相互分离的质心，即，下一个质心点总是离上一个质心点较远的点。

04 KNN三要素

距离度量、k值、分类决策规则，是k近邻法地三要素，下面分别介绍。

距离度量
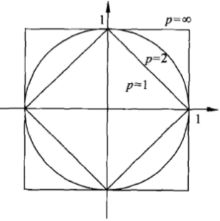
衡量特征空间中两个实例点的距离，度量方法一边用Lp距离，p取不同值时，分别有不同地名称，常用欧氏距离作为距离度量。

• Lp距离

• 欧氏距离(p=2)

• 曼哈顿距离(p=1)

• p无穷

不同的距离度量，得到的实例点之间的距离是不同的，下面的图给出了二维空间中，p取不同值时，与原点的Lp距离为1的点的集合图形，可以看到，欧氏距离对应的是圆。

k值

k值得选择，反映了对近似误差与估计误差之间的权衡。

• 近似误差
  类比于训练误差，关注训练集。近似误差越小，说明模型对训练集的预测越好，但近似误差过小容易出现过拟合，降低模型对于测试集的预测准确性。

• 估计误差
  类比于测试误差，关注测试集。估计误差越小，说明模型对未知数据预测越好，模型越接近真实模型，过小的近似误差会导致模型过拟合，使得模型对于未知数据的预测变差（估计误差变大）

• k值过小

  • 近似误差会减小，估计误差会增大
  • 易产生过拟合
  • 噪声敏感：如果邻近的实例点恰好是噪声，预测就会出错。

• k值过大

  • 可以减少估计误差，但近似误差会增大
  • 极端情况，k=样本点数N，无论输入实例如何，都将被简单归为训练集中最多的类，忽略了大量有用信息

分类决策规则

k近邻法中得分类决策规则，常用多数表决法，当然，为了弱化k值的影响，还可以采用加权表决法。

• 多数表决

  • 由输入实例的k个邻近的训练实例中的多数类决定输入实例的类
  • 不考虑距离加权影响，每个投票权重都为1

• 加权表决

  • 由输入实例的k个邻近的训练实例中的多数类加权决定输入实例的类
    -即根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）

为什么要使用多数表决法呢，这里给出多数表决法的直观解释，这个解释我给满分！

05 kd树（二叉树）

了解了k近邻法后，你应该会产生这样的疑惑：

如何对训练数据进行快速k近邻搜索？

难道用线性扫描么？

要计算输入实例与训练集每一个实例的距离，当训练集很大时，计算非常耗时，不可取

面对大数据量的训练集，人们想出了一个好办法提高搜索效率：

使用特殊的数据结构存储训练数据，以减少计算距离的次数，这就是——kd树

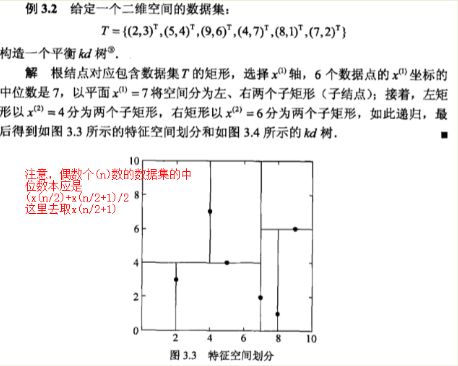
下面结合示例，讲解如何构造kd树以及如何搜索kd树

• 构造kd树
  

• 示例-构造kd树
  

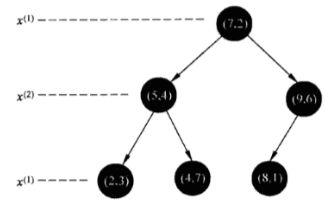
一波操作之后，得到的kd树直观理解长成这样：

• 搜索kd树
  

• 示例-搜索kd树
  

06 总结

本文详细讲解了KNN算法，并与K-Means、K-Means++算法进行了对比，给出了KNN算法的三要素，最后介绍了便于KNN算法实现的kd树的数据存储结构。

• k近邻法过程
  对给定的训练实例点和输入实例点，首先确定输入实例点的k个最近邻训练实例点，然后利用这k个训练实例点的类的多数（距离加权）来预测输入实例点的类

• k近邻法三要素
  距离度量、k值选择、分类决策规则

• kd树
  一种对k维空间中的实例点进行存储，以便对其进行快速检索的树形数据结构（这里的k维与k近邻的k意义不同）

下期将详细介绍另一种常用的分类方法：朴素贝叶斯，敬请期待~~

---

07 参考

《统计学习方法》 李航 Chapter3