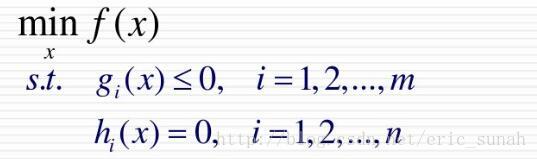程序员的机器学习入门笔记(八):最优化与计算复杂度概述
最优化定义
无论做何事,人们总希望用最小的代价来取得最大的收益,为此人们发明了各种各样的数据工具(导数,微积分),并尝试使用这些知识来最优化解决实际问题。但是在解决实际问题最优化解的时候,经常是伴随着两个重要的特征
- 多元化:事物的发展受到多种因素的影响
- 非线性:发展规律是非线性的
为了解决上面的两个问题,二战后线性规划诞生了
最优化数学定义
最优化问题是应用数学的重要研究领域。它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称
约束条件数学模型:
X为n维向量,为实际运用中的解。
s.t.为英文subject to的缩写,表示受限于。
f(x)称为目标函数,如上式,我们要求f(x)的最小值。
h(x)为等式约束;g(x)为不等式约束。
根据目标函数与约束函数的不同形式,把最优化问题分为下面几种不同的类型
- 线性规划:f(x),h(x),g(x)都是线性函数
- 非线性规划:f(x),h(x),g(x)任意一个是非线性的
- 二次规划:f(x)为二次函数,h(x),g(x) 为线性函数
- 多目标规划:f(x)是向量函数
凸集分离定理
凸集分离定理是应用凸集到最优化理论中的重要结果,这个结果在最优化理论中有重要的位置
凸集的定义
如果一个集合X是凸集,则该集合钟的任意两个点X1和X2连成一条线段,该线段上的任意一点也位于X中
凸集分离的定义
凸集分离定理是应用凸集到最优化理论中的重要结果,这个结果在最优化理论中有重要的位置。所谓两个凸集分离,直观地看是指两个凸集合没有交叉和重合的部分,因此可以用一张超平面将两者隔在两边。
凸集分离的意义
凸集分离的意义在于,为分类提供了理论上的开端,在机器学习的分类问题钟,可以把带有类别标签的训练集看成是不同的凸集,而分隔他们的超平面就是分类器。
凸函数
凸函数,是数学函数的一类特征。凸函数就是一个定义在某个向量空间的凸子集C(区间)上的实值函数。设f(x)在[a,b]上连续,若对[a,b]中任意两点x1,x2,恒有 f[(x1+x2)/2]>=[f(x1)+f(x2)]/2则称 f(x) 在[a,b] 上是向上凸的,简称上凸.f(x)是[a,b]上的凸函数。
凸函数有两个重要的性质
- 对于凸函数来说,局部最小值就是全局最小值。
- 对于凸函数来说,局部最优解就是全局最优解
在最优化理论中,局部最优被称为满意解,全局最优被称为最优解。如果能够由一个凸函数构造出一个待优化问题的数学模型,那么就可以通过寻找这个凸函数的唯一极值点来求解最优化问题
下面列举几个常见的凸函数
- 线性函数,仿射函数
- 最大值函数
- 幂函数
- 对数函数
- 指数和的对数
- 几何平均
- 范数
局部最优与全局最优
现实中,目标函数经常会具有多个极小值,每个最小值都是一个局部最小值,对于这种情况,大多数算法都能只能保证找到满意解,例如下面这种情况
为了避免陷入局部最优,人们会尽可能使用凸函数作为优化问题的目标函数(例如Logistic函数),凸优化是求全局最优解最方便的工具之一,机器学习中使用最优化方法求解的目标函数基本都是凸函数,例如:Logistic,神经网络中的各类激活函数,深度学习,支持向量机的核函数等
对于无法转换为凸函数的优化问题,例如上面图的那种情况,在数据集不是很大的情况下可以通过穷举来算出所有的值,对于数据集较大时,一般采取随机优化的方法,不同的问题可能会有不同的方法,例如 模拟退火算法用来解决最短路径的问题,隐马尔科夫链算法用来解决自然语言处理语音识别的问题
计算复杂度与NP问题
显示生活中的大多数问题的数据集都是离散的数据集,为了反映统计规律有时候数据量很大,而且多数目标函数都是不能简单的求得解析解,这就带来了一个问题:算法的复杂性问题
为了对数据进行快速而有效的计算,很多数据的分析算法被发明出来,根据算法的时间复杂度可以把问题分为两类
- 易解问题:使用多项式时间算法可以解决的问题
- 难解问题:使用指数时间算法可以解决的问题,这类问题的数据规模不大,却要执行相当长的时间
多项式时间的问题规模表达:
LogN,N,NLogN,N^2,N^3指数时间的问题规模表达:
2^N,N!除了问题规模预运算时间的比较,衡量一个算法还需要考虑确定性和非确定性。
- 确定性:针对自动机模型,根据当时的状态和输入,自动机的状态转移是唯一的,程序在每个状态转移时,产生下一步的结果是唯一的
- 非确定性:在每个时刻,如果自动机有多个状态可供选择,并尝试执行每个可选择的状态,执行路径是并行的,所有路径都可能返回结果
自动机(Automata Machine):是一种基于状态变化进行迭代的算法,通常把这类算法看成一种机器,例如 图灵机,有限状态机,玻尔兹曼机,支持向量机等
非确定性算法可能会陷入局部最优,因为所有并行路径中某个执行路径达到最优算法就会结束,但此时并不一定是全局最优
有了时间以及状态转移的两个概念基础,问题的计算复杂度可以分为以下几种
- P问题:可以用多项式时间的确定性算法对该问题进行求解,前面几篇博客中的算法大多数属于这类
- NP问题:可以用多项式时间的非确定性算法对该问题进行求解
- NP完全性问题:属于NP的子类,该类问题是NP类中最复杂的问题,其中任何一个问题,至今都没有找到多项式时间的算法
机器学习中大多数算法都是针对NP类问题的,下面列出一些常见的NP类问题
- 背包问题:背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?它是在1978年由Merkel和Hellman提出的。
- 最短路径问题:最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径
- 旅行推销问题:旅行商问题,即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。该问题可以通过模拟退火算法进行求解
- 最大团问题:最大团问题(Maximum Clique Problem, MCP)是图论中一个经典的组合优化问题,也是一类NP完全问题,在国际上已有广泛的研究,而国内对MCP问题的研究则还处于起步阶段,因此,研究最大团问题具有较高的理论价值和现实意义。
- 图同构问题:两图同构的直觉条件是:若其中一图可以由移动顶点使它与另外一图重合,则为同构
总结
从本博客开始的基本都是介绍非确定性算法为主,机器学习的高级算法大多数都是针对NP类问题,即算法的状态转移具有非确定性,产生的结果允许在一定的误差范围内,最优化理论和机器学习的多年研究,很大程度上为这类问题提供了解决方法。