100-Days-Of-ML系列Day3

今天来学习多元线性回归。多元线性回归与简单线性回归类似，都是尝试通过一个线性函数来拟合数据，不同的是，多元线性回归的自变量包含两个或两个以上的特征。
首先给出多元线性回归的一般模型： hθ(x)=θ0+θ1x1+⋯+θnxn h θ ( x ) = θ 0 + θ 1 x 1 + ⋯ + θ n x n ,写成矩阵形式就是 hθ(x)=∑i=0nθixi=θTx h θ ( x ) = ∑ i = 0 n θ i x i = θ T x 。
多元线性回归模型有以下假定：

1. 零均值假定，随机误差项 μ μ 均值为0。
2. 同方差假定，随机误差项 μ μ 方差为同一常数。
3. 无自相关性，即 Cov(μi,μj)=0,(i≠j,i,j=1,2,⋯,n) C o v ( μ i , μ j ) = 0 , ( i ≠ j , i , j = 1 , 2 , ⋯ , n ) 。
4. 随机误差项与x不相关。
5. 随机误差项服从均值为0，方差为 σ2 σ 2 的正态分布。
6. 解释变量x之间不存在多重共线性。

基于这些假设，我们可以用最小二乘拟合多元线性回归模型，这里最小二乘与最大似然法是等价的。
对于多元线性回归模型： y(i)=θTx(i)+ε(i) y ( i ) = θ T x ( i ) + ε ( i ) ，根据上面的假设，我们有： p(ε(i))=12π√σexp(−(ε(i))22σ2) p ( ε ( i ) ) = 1 2 π σ exp ⁡ ( − ( ε ( i ) ) 2 2 σ 2 ) ，即 p(y(i)∣∣x(i);θ)=12π√σexp(−(y(i)−θTx(i))22σ2) p ( y ( i ) | x ( i ) ; θ ) = 1 2 π σ exp ⁡ ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 )
所以似然函数为： L(θ)=∏i=1mp(y(i)∣∣x(i);θ)=∏i=1m12π√σexp(−(y(i)−θTx(i))22σ2) L ( θ ) = ∏ i = 1 m p ( y ( i ) | x ( i ) ; θ ) = ∏ i = 1 m 1 2 π σ exp ⁡ ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 )
对数似然函数：

上式中减号前面为常数项，最大化似然函数即为最小化求和项，故将求和项的相反数作为为我们的目标函数： J(θ)=12∑i=1m(hθ(x(i))−y(i))2=12(Xθ−y)T(Xθ−y) J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 ( X θ − y ) T ( X θ − y )
求梯度：

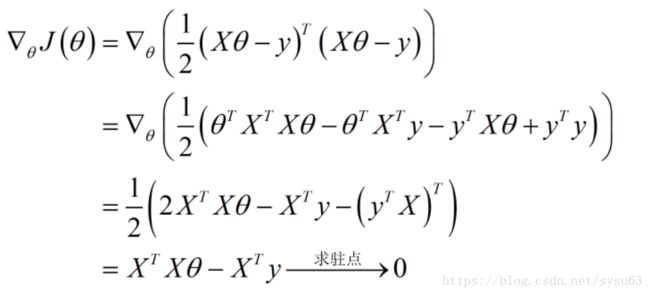
得到参数的解析式： θ=(XTX)−1XTy θ = ( X T X ) − 1 X T y
得到的结果与最小二乘的结果完全一样，故二者在这个模型中是等价的。
当然，在实际运用中，我们会对自变量x进行选择，选择方法包括向前选择法、向后选择法、向前向后法。
在求解过程中会加入一些正则项防止过拟合。求解也很简单，只要适当地改造我们的目标函数即可。详细内容见我的另一篇博客，回归。
介绍完理论，下面就按照给出的代码，用python实现简单的多元回归模型。

第一步 数据预处理

导入相应的库

import pandas as pd
import numpy as np

读取数据

dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[ : , :-1].values
Y = dataset.iloc[ : ,  4 ].values

数据处理

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[: , 3] = labelencoder.fit_transform(X[ : , 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()

onehot编码之后会产生共线性，所以需要把其中一列去掉。

X = X[: , 1:]

切分数据集

from sklearn.cross_validation import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)

拟合模型

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)

预测测试集的结果

y_pred = regressor.predict(X_test)

结果对比：

可以看到预测结果和真实结果还是有一定差距的，说明我们的模型还不是太完美。