100-Days-Of-ML系列Day
今天继续学习机器学习算法——KNN。
KNN是通过测量不同特征值之间的距离进行分类的一种算法。它的思路是:如果一个样本在特征空间的k个最相似(即特征空间中最近邻)的样本大多数属于某一个类别,则该样本也属于这个类别,其中k通常是不大于20的整数。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别决定待分样本所属的类别。
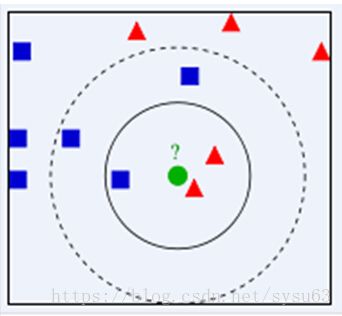
下面通过一个简单的例子说明一下:如下图,要确定绿色圆属于哪个类别。假设k取3,则绿色圆的最近样本为实线圆圈,其中红色三角形占2/3,蓝色四方形占1/3,则认为绿色圆属于红色三角形的类别。当k取5时,绿色圆的最近样本为虚线圆圈,其中红色三角形占2/5,蓝色四方形占3/5,则认为绿色圆属于蓝色四方形的类别。
总结一下,KNN算法的具体步骤如下:
- 计算距离:给定分类对象,计算它与训练集中每个样本的距离
- 找最近邻:找出与分类对象最近的k个训练样本,作为分类对象的最近邻
- 确定类别:根据这k个最近邻的主要类别作为分类对象的类别
从上面的步骤我们可以看到,计算距离是KNN算法中的核心模块,下面介绍几种常用的距离计算方法:
-
欧式距离 d i s t ( X , Y ) = ∑ i = 1 n ( x i − y i ) 2 dist\left( {X,Y} \right) = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} } dist(X,Y)=i=1∑n(xi−yi)2
欧式距离是最常见的距离度量,衡量多维空间中各个点之间的绝对距离。
因为计算是基于各维度特征的绝对数值,所以欧式距离需要保证各指标在相同的刻度级别,比如对身高(cm)和体重(kg)两个单位不同的指标使用欧式距离可能使结果失效。 -
曼哈顿距离 d i s t ( X , Y ) = ∑ i = 1 n ∣ x i − y i ∣ dist\left( {X,Y} \right) = \sum\limits_{i = 1}^n {\left| {{x_i} - {y_i}} \right|} dist(X,Y)=i=1∑n∣xi−yi∣
曼哈顿距离来源于城市区块距离,是将多个维度上的距离进行求和后的结果 -
切比雪夫距离 d i s t ( X , Y ) = lim p → ∞ ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p = max ∣ x i − y i ∣ dist\left( {X,Y} \right) = \mathop {\lim }\limits_{p \to \infty } {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^p}} } \right)^{1/p}} = \max \left| {{x_i} - {y_i}} \right| dist(X,Y)=p→∞lim(i=1∑n∣xi−yi∣p)1/p=max∣xi−yi∣
-
明可夫斯基距离 d i s t ( X , Y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p dist\left( {X,Y} \right) = {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^p}} } \right)^{1/p}} dist(X,Y)=(i=1∑n∣xi−yi∣p)1/p
上面的欧式距离、曼哈顿距离和切比雪夫距离都是明可夫斯基距离在特殊条件下的应用。 -
马哈拉诺比斯距离
既然欧式距离无法忽略指标度量的差异,所以使用欧式距离之前需要对底层指标进行数据的标准化,而基于各指标维度进行标准化后再使用欧式距离就衍生出另外的一个距离度量——马哈拉诺比斯距离(Mahalanobis Distance),简称马氏距离。
下面总结一下KNN算法的优缺点:
优点
- 简单、有效。
- 重新训练的代价较低
- 计算时间和空间线性于训练集的规模
- 由于KNN方法主要靠周围有限的近邻样本,而不是靠判别类域的方法来确定所属类别,因此对于类域交叉或重叠较多的待分样本集来说,KNN方法较其他方法更合适。
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
缺点: