独家连载 | 误差反向传播算法推导

4.5 BP网络模型和公式推导

4.5.1BP网络模型

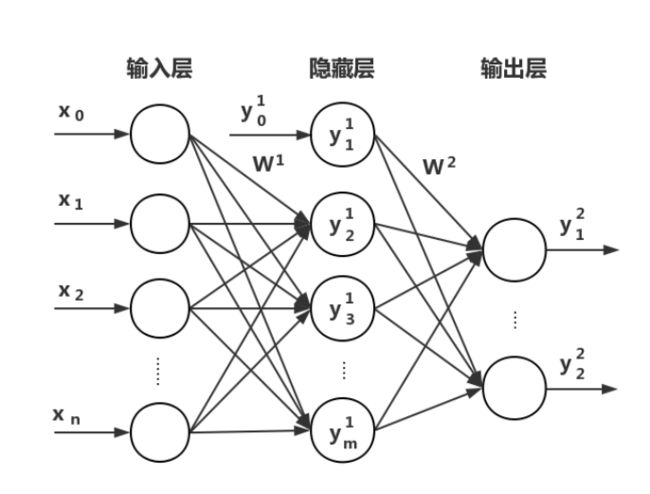
假设我们有一个2层(统计神经网络层数的时候一般输入层忽略不计)的神经网络如图4.17所示：

该网络的输入向量为X = （x₁，x₂，…，x_i，…，x_n），图中x₀ = 1表示输入层偏置值。隐藏层输出向量为$Y^1=(y_1^1,y_2^1,\dots ,y_j^1,\dots ,y_m^1)$，图中$y_0^1=1$表示隐藏层偏置值。输出层输出向量为$Y^2=(y_1^2,y_2^2,\dots ,y_k^2,\dots ,y_l^2)$。期望输出$T=(t_1,t_2,\dots ,t_k,\dots ,t_l)$。输入层到隐藏层之间的权值用矩阵W₁表示，W¹_ij表示W₁矩阵中第i行第j列的权值。隐藏层到输出层之间的权值用矩阵W₂表示，W²_jk表示W₂矩阵中第j行第k列的权值。另外我们定义net¹为隐藏层中权值乘以输入层信号的总和，net¹_j表示隐藏层中第j个神经元得到的输入信号总和。net²为输出层中权值乘以隐藏层信号的总和，net²_k表示输出层中第k个神经元得到的输入信号总和。

对于隐藏层有：
$ne{t}_j^1={\sum }_{i=0}^n{w}_{ij}^1{x}_i；(j=1,2,...,m)$

$y_j^1=f(ne{t}_j^1)；(j=1,2,...,m)$

对于输出层有：
$ne{t}_k^2={\sum }_{i=0}^n{w}_{jk}^2{y}_j^1；(k=1,2,...,l)$

KaTeX parse error: \tag works only in display equations

公式4.13和4.15中的激活函数假设我们都使用sigmoid函数，sigmoid函数的公式在上文中的公式4.8。sigmoid函数具有连续、可导的特点，它的导数为：
$$f^{\prime }(x)=f(x)[1-f(x)]$$

4.5.2BP算法推导

根据上文中提到的代价函数，当网络输出与期望输出不同时，会存在输出误差E，为了简单我们只计算一个样本的均方差公式，如果是计算多个样本可以求所有样本代价函数的平均值。一个样本的均方差公式定义如下：
$$E=\frac{1}{2}(T-Y^2{)}^2=\frac{1}{2}\sum _{k=1}^l(t_k-y_k^2{)}^2$$

将以上误差定义式展开至隐藏层：
$$E=\frac{1}{2}\sum _{k=1}^l[t_k-f(ne{t}_k^2){]}^2=\frac{1}{2}\sum _{k=1}^l{\left[t_k-f\left(\sum _{j=0}^m{w}_{jk}^2{y}_j^1\right)\right]}^2$$

再进一步展开至输入层：
$$E=\frac{1}{2}\sum _{k=1}^l{\left[t_k-f\left(\sum _{j=0}^m{w}_{jk}^{2}f(ne{t}_j^1)\right)\right]}^2=\frac{1}{2}\sum _{k=1}^l{\left[t_k-f\left(\sum _{j=0}^m{w}_{jk}^{2}f\left(\sum _{j=0}^m{w}_{ij}^1{x}_i\right)\right)\right]}^2$$

从公式4.18和4.19中可以看出，网络的误差E是跟神经网络各层权值W¹_ij和W²_jk相关的，因此调整各层的权值，就可以改变误差E的值。我们的目标就是要得到比较小的误差值，所以我们可以采用梯度下降法来最小化误差E的值。根据梯度下降法，我们可以得到：
$$\Delta w_{ij}^1=-\eta \frac{\delta E}{\delta w_{ij}^1}$$
$$i=0,1,2,\dots ,n;j=1,2,\dots ,m$$

$$\Delta w_{ij}^2=-\eta \frac{\delta E}{\delta w_{jk}^2}$$
$$j=0,1,2,\dots ,m;k=1,2,\dots ,l$$
在下面的推导过程中均默认对于隐藏层有i =0，1，2，…，n；j = 1，2，…，m；对于输出层有：j =0，1，2，…，m；k = 1，2，…，l。

根据微积分的链式法则可以得到，对于隐藏层有：
$$\Delta w_{ij}^1=-\eta \frac{\delta E}{\delta w_{ij}^1}=-\eta \frac{\delta E}{\delta ne{t}_j^1}\frac{\delta ne{t}_j^1}{\delta w_{ij}^1}$$

根据微积分的链式法则可以得到，对于输出层有：
$$\Delta w_{jk}^2=-\eta \frac{\delta E}{\delta w_{jk}^2}=-\eta \frac{\delta E}{\delta ne{t}_k^2}\frac{\delta ne{t}_k^2}{\delta w_{jk}^2}$$

我们可以定义一个误差信号，命名为δ(delta)，令：
$${\delta }_j^1=-\frac{\delta E}{\delta ne{t}_j^1}$$

$${\delta }_k^1=-\frac{\delta E}{\delta ne{t}_k^2}$$

综合公式4.12,4.22,4.24，可以得到输入层到隐藏层的权值调整公式为：
$$\Delta w_{ij}^1=\eta {\delta }_j^1{x}_i$$

综合公式4.14,4.23,4.25，可以得到隐藏层到输出层的权值调整公式为：
$$\Delta w_{jk}^2=\eta {\delta }_k^2{y}_j^1$$

可以看出在公式4.26和4.27中，只要求出δ¹_j和δ²_k的值，就可以计算出Δw¹_ij和Δw²_jk的值了。

对于隐藏层，δ¹_j可以展开为：
$${\delta }_j^1=-\frac{\delta E}{\delta ne{t}_j^1}=-\frac{\delta E}{\delta y_j^1}\frac{\delta y_j^1}{\delta ne{t}_j^1}=-\frac{\delta E}{\delta y_j^1}{f}^{\prime }(ne{t}_j^1)$$

对于输出层，δ²_k可以展开为：
$${\delta }_k^2=-\frac{\delta E}{\delta ne{t}_k^2}=-\frac{\delta E}{\delta y_k^2}\frac{\delta y_k^2}{\delta ne{t}_k^2}=-\frac{\delta E}{\delta y_k^2}{f}^{\prime }(ne{t}_k^2)$$

在公式4.28和4.29中，求网络误差对各层输出的偏导，对于输出层：
$$\frac{\delta E}{\delta y_k^2}=-(t_k-y_k^2)$$

对于隐藏层：
$\frac{\delta E}{\delta y_j^1}=\frac{\delta \frac{1}{2}{\sum }_{k=1}^l[t_k-f({\sum }_{j=0}^m{w}_{jk}^2{y}_j^1){]}^2}{\delta y_j}=-{\sum }_{k=1}^l\left(t_k-f\left({\sum }_{j=0}^m{w}_{jk}^2{y}_j^1\right)\right)f^{\prime }\left({\sum }_{j=0}^m{w}_{jk}^2{y}_j^1\right)w_{jk}^2=-{\sum }_{k=1}^l(t_k-y_k^2)f^{\prime }(ne{t}_k^2)w_{jk}^2$

将公式4.30带入公式4.29，再根据sigmoid函数的求导公式4.16，可以得到：
${\delta }_k^2=-\frac{\delta E}{\delta y_k^2}{f}^{\prime }(ne{t}_k^2)=(t_k-y_k^2)y_k^2(1-y_k^2)$

${\delta }_j^1=-\frac{\delta E}{\delta y_j}{f}^{\prime }(ne{t}_j^1)=\left({\sum }_{k=1}^l(t_k-y_k^2)f^{\prime }(ne{t}_k^2)w_{jk}^2\right)f^{\prime }(ne{t}_j^1)=\left({\sum }_{k=1}^l(t_k-y_k^2)y_k^2(1-y_k^2)w_{jk}^2\right)f^{\prime }(ne{t}_j^1)=\left({\sum }_{k=1}^l{\delta }_k^2{w}_{jk}^2\right)y_j^1(1-y_j^1)$

将公式4.32带入4.27中，得到隐藏层到输出层权值调整：
$\Delta w_{jk}^2=\eta {\delta }_k^2{y}_j^1=\eta (t_k-y_k^2)y_k^2(1-y_k^2)y_j^1$

将公式4.33带入4.26中，得到输入层到隐藏层权值调整：
$\Delta w_{ij}^1=\eta {\delta }_j^1{x}_i=\eta \left({\sum }_{k=1}^l{\delta }_k^2{w}_{jk}^2\right)y_j^1(1-y_j^1)x_i$

对于一个多层的神经网络，假设一共有h个隐藏层，按顺序将各隐藏层节点数分别记为：m₁，m₂，…，m_h，输入神经元个数为n，输出神经元个数为l；各隐藏层输出分别记为：Y¹，Y²，…，Y^h，输入层的输入记为：X，输出层的输出记为：Y^h+1；各层权值矩阵分别记为：W¹，W²，…，W^h+1，W¹表示输入层到一个隐藏层的权值矩阵，W^h+1表示最后一个隐藏层到输出层的权值矩阵；各层学习信号分别记为：δ¹，δ²，…，δ^h+1，δ^h+1表示输出层计算出的学习信号；则各层权值调整计算公式为（如下分类）
对于输出层：
$\Delta w_{jk}^{h+1}=\eta {\delta }_k^{h+1}{y}_j^h=\eta (t_k-y_k^{h+1})y_k^{h+1}(1-y_k^{h+1})y_j^h(j=0,1,2,...,m_h;k=1,2,...,l)$

对于第h隐藏层：
$\Delta w_{ij}^h=\eta {\delta }_j^h{y}_i^{h-1}=\eta \left({\sum }_{k=1}^l{\delta }_k^{h+1}{w}_{jk}^{h+1}\right)y_j^h(1-y_j^h)y_j^{h-1}(i=0,1,2,...,m_{h-1};j=1,2,...,m_h)$

按照以上规律逐层类推，则第一个隐藏层的权值调整公式为：
$\Delta w_{pq}^1=\eta {\delta }_q^1{x}_p=\eta ({\sum }_{r=1}^{m_2}{\delta }_r^2{w}_{qr}^2)y_q^1(1-y_q^1)x_p(p=0,1,2,...,n;j=1,2,...,m_1)$

4.5.3BP算法推导的补充说明

我们已经从头到尾详细推导了一遍BP算法的整个流程，在这一小节中对BP算法再做两点补充说明：
1.网络的偏置值。
在上文中我们的推导过程一直是使用权值w来进行计算的，如果我们把偏置值独立出来，那么偏置值的参数应该怎么调整呢？

我们可以看到公式4.26以及4.27，在公式4.26中，把i的取值设置为0，并且我们知道x₀ = 1，所以我们可以得到：
$\Delta b_j^1=\eta {\delta }_j^1$

在公式4.26中，把j的取值设置为0，并且我们知道y₀ = 1，所以我们可以得到：
$\Delta b_k^2=\eta {\delta }_k^2$
如果是把偏置值单独拿出来计算的话就是公式4.39和4.40的表达式。

2.用矩阵形式来表达BP学习算法。
下面我们直接给出BP学习算法矩阵表达形式的结果，具体推导过程跟上文中的推导过程类似，不过会涉及到矩阵求导的相关知识，大家有兴趣的话可以自己推导一下。如果是把BP学习算法写成矩阵的形式来表达，假设一共有h个隐藏层。输入数据的矩阵为X，X中的每一行表示一个数据，列表示数据的特征。比如我们一次性输入3个数据，每个数据有4个特征，那么X就是一个3行4列的矩阵。

各隐藏层输出分别记为：Y¹，Y²，…，Y^h，输出层的输出记为：Y^h+1。Y中的每一个行表示一个数据的标签。比如我们有3个数据，每个数据有1个标签，那么Y就是一个3行1列的矩阵。

各层权值矩阵分别记为：W¹，W²，…，W^h+1，W¹表示输入层到一个隐藏层的权值矩阵，W^h+1表示最后一个隐藏层到输出层的权值矩阵。权值矩阵的行等于前一层的神经元个数，权值矩阵的列对应于后一层的神经元个数。比如在输入层和第一个隐藏层之间的权值矩阵是W¹，输入层有3个神经元，第一个隐藏层有10个神经元，那么W¹就是一个3行10列的矩阵。

各层学习信号分别记为：δ¹，δ²，…，δ^h+1。δ^h+1表示输出层计算出的学习信号。

对于输出层的学习信号δ^h+1：
${\delta }^{h+1}=(T-Y^{h+1})\circ f^{\prime }(Y^h{W}^{h+1})=(T-Y^{h+1})\circ Y^{h+1}\circ (1-Y^{h+1})$

公式4.41中的“ ∘ ”符号是element-wise multiplication，意思是矩阵中的元素对应相乘。例如下面的例子：

对于第h隐藏层的学习信号δ^h：
${\delta }^h={\delta }^{h+1}(W^{h+1}{)}^T\circ f^{\prime }(Y^{h-1}{W}^h)={\delta }^{h+1}(W^{h+1}{)}^T\circ Y^h\circ (1-Y^h)$

对于第1隐藏层的学习信号δ¹：
${\delta }^1={\delta }^2(W^2{)}^T\circ f^{\prime }(X{W}^1)={\delta }^2(W^2{)}^T\circ Y^1\circ (1-Y^1)$

对于输出层的权值矩阵W^h+1：
$\Delta W^{h+1}=\eta (Y^h{)}^T{\delta }^{h+1}$

对于第h隐藏层权值矩阵W^h：
$\Delta W^h=\eta (Y^{h-1}{)}^T{\delta }^h$

对于第1隐藏层权值矩阵W¹：
$\Delta W^1=\eta (X{)}^T{\delta }^1$

作者介绍