李弘毅老师GAN笔记（六），WGAN / EBGAN

1、JS-divergence 的问题

在原始 GAN 中，使用的 JS-divergence 存在一些问题，这里介绍其中的一个问题。在图像所在的高维空间中，生成的图像分布和真实图像的分布可能是完全没有重叠的，比如在三维空间举一个例子，可以理解为两者的分布是三维空间中的两个面，那么他们重叠的部分几乎为零。那么这样 JS-divergence 的问题就出现了。
如下图所示， PG0 P G 0 与 Pdata P d a t a 如果没有交集，那么无论间隔多远，算出来的 JS-divergence 都是 log2

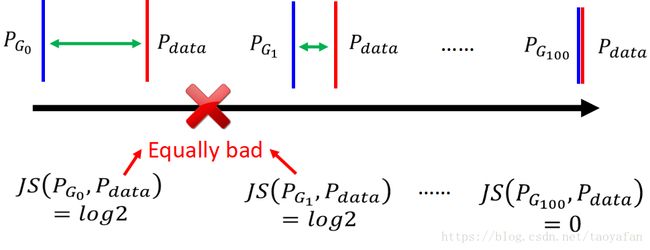
这个问题的其中一个原因是因为 GAN 的判别网络是用的 sigmoid 函数，如果训练的太好的话会导致梯度消失。如下图所示：

如果判别网络训练的太好，则在真实数据和生成数据的部分微分是0，所以要保证判别网络不能训练的太好，然后再训练生成网络。
有一个方法就是不用 sigmoid 函数，改用线性函数。这个就是 LSGAN。

2、WGAN 原理

有一种解决方法就是想办法衡量两个分布的距离，这便是 WGAN 要解决的问题，它提出的衡量两个分布的距离的方法是，将一个分布的值进行移动，使得移动后的新的分布和另一个分布相同，需要移动的最短距离就是 WGAN 提出的衡量的距离的方法，这个距离叫做 Wasserstein distance，我上边的解释可能不是很容易理解，先放一张图，再解释可能容易理解些。

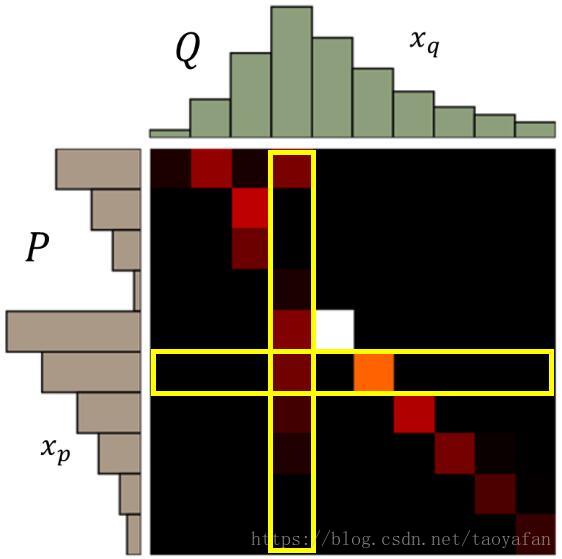
左边是分布 P ,上边是分布 Q，如果是衡量从将 P 分布移动的和 Q 移动的一样，则横着看，第 (i,j) 个方格表示从 P(i) 移动到 Q(j) 的量的大小，颜色越浅表示移动的越多。
则总距离表示为

B(λ)=∑xp,xqγ(xq,xq)||xq−xq|| B ( λ ) = ∑ x p , x q γ ( x q , x q ) | | x q − x q | |

则 Wasserstein distance 表示为

W(P,Q)=minγB(γ) W ( P , Q ) = min γ B ( γ )

使用 Wasserstein distance 便可以衡量两个完全没有交集的分布的距离了。

3、 WGAN 实现

经过推导后，WGAN 的公式如下：

V(G,D)=maxD∈1−Lipschitz{Ex∼Pdata[D(x)]−Ex∼PG[D(s)]} V ( G , D ) = max D ∈ 1 − L i p s c h i t z { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( s ) ] }

1-Lipschitz 是什么下边再讲，上边的公式就是希望 x 从真实数据中采样出的期望越大越好，而从生成数据中采样出的期望越小越好。
所谓 k-Lipschitz，就是指函数满足下边的要求：

||f(x1)−f(x2)||≤K||x1−x2|| | | f ( x 1 ) − f ( x 2 ) | | ≤ K | | x 1 − x 2 | |

其实就是斜率不大于 K，那么 1-Lipschitz 就是指斜率不大于 1。
在原始的 WGAN 中没有详细介绍如何求解这个 V(G, D)，只是给出了一种可以实现的方法（weight clipping）：设定一个参数 c，当 w 大于 c 时设定为 c，小于 -c 时设定为 -c，但是这个并没有将 D 限制为 1-Lipschitz，下边给出改进版的WGAN。

4、Improved WGAN（WGAN-GP）

GP 的全称为 gradient penalty，看完下面的介绍会明白这两个词的意思的。
前面提到了一个问题，及这个 1-Lipschitz 怎么实现，在 WGAN-GP 又给出了一种方法：要求 D 为 1-Lipschitz 的函数也就是 D(x) 对 x 的梯度在取所有的 x 时都小于1 ，所以在目标函数后面加一个正则项，目标函数变为：

V(G,D)=maxD{Ex∼Pdata[D(x)]−Ex∼PG[D(s)]−λ∫xmax(0,||∇xD(x)−1||)dx} V ( G , D ) = max D { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( s ) ] − λ ∫ x m a x ( 0 , | | ∇ x D ( x ) − 1 | | ) d x }

.
但是要所有的 x 都满足是不可能的，所以提出了 penalty 这个范围，只要求这个范围的 x 满足。而 penalty 为 PG P G 中采样的数据和 Pdata P d a t a 采样的数据的连线中取一个随机的采样，也就是只要 PG P G 和 Pdata P d a t a 中间这个范围的 D 满足 1-Lipschitz 就行了。
在实际上做的时候，希望 ||∇xD(x)|| | | ∇ x D ( x ) | | 越接近 1 越好，所以实作时时候的目标函数为：

V(G,D)=maxD{Ex∼Pdata[D(x)]−Ex∼PG[D(s)]−λEx∼Ppenalty(||∇xD(x)−1||)2 V ( G , D ) = max D { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( s ) ] − λ E x ∼ P p e n a l t y ( | | ∇ x D ( x ) − 1 | | ) 2

.
但是直觉上也还会存在一些问题，比如从 PG P G 到 Pdata P d a t a 更新的实际路线可能是曲线，但是是用 penalty 的话是用的是两者的连线即可能不是实际上更新的路线。

5、Spectrum Norm

这个方法可以使得 D(x) 的梯度的范数在任何地方都是小于 1 的。
课上没有仔细讲，祥见paper：
Takeru Miyato, Toshiki Kataoka, Masanori Koyama, Yuichi Yoshida, Spectral Normalization for Generative Adversarial Networks, ICLR, 2018

6、Energy-based GAN（EBGAN）

把 Discriminator 个结构改了一下，如下图所示：

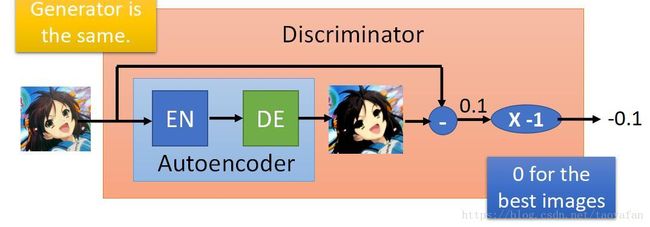
直接改成了一个 Autoencoder， 输出的结果就是 Autoencoder 的值乘个负号。这个的好处就是可以提前训练判别网络。