深入理解Cache
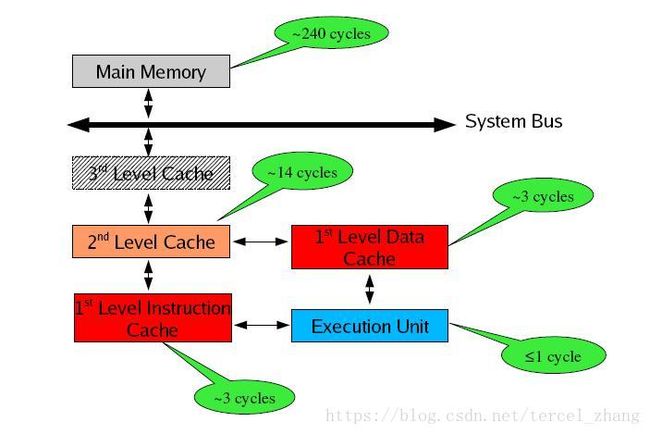
存储器是分层次的,离CPU越近的存储器,速度越快,每字节的成本越高,同时容量也因此越小。寄存器速度最快,离CPU最近,成本最高,所以个数容量有限,其次是高速缓存(缓存也是分级,有L1,L2等缓存),再次是主存(普通内存),再次是本地磁盘。
寄存器的速度最快,可以在一个时钟周期内访问,其次是高速缓存,可以在几个时钟周期内访问,普通内存可以在几十个或几百个时钟周期内访问。
(注 本图来自Ulrich Drepper大牛的讲稿,如有侵权,通知即删)
存储器分级,利用的是局部性原理。我们可以以经典的阅读书籍为例。我在读的书,捧在手里(寄存器),我最近频繁阅读的书,放在书桌上(缓存),随时取来读。当然书桌上只能放有限几本书。我更多的书在书架上(内存)。如果书架上没有的书,就去图书馆(磁盘)。我要读的书如果手里没有,那么去书桌上找,如果书桌上没有,去书架上找,如果书架上没有去图书馆去找。可以对应寄存器没有,则从缓存中取,缓存中没有,则从内存中取到缓存,如果内存中没有,则先从磁盘读入内存,再读入缓存,再读入寄存器。
本系列的文章重点介绍缓存cache。了解如何获取cache的参数,了解缓存的组织结构,了解cache对程序的影响,了解如何利用cache提升性能。
本文作为系列文章的第一篇,讲述的如何获取cache的组成结构和如何获取cache的参数。
cache分成多个组,每个组分成多个行,linesize是cache的基本单位,从主存向cache迁移数据都是按照linesize为单位替换的。比如linesize为32Byte,那么迁移必须一次迁移32Byte到cache。 这个linesize比较容易理解,想想我们前面书的例子,我们从书架往书桌搬书必须以书为单位,肯定不能把书撕了以页为单位。书就是linesize。当然了现实生活中每本书页数不同,但是同个cache的linesize总是相同的。
所谓8路组相连( 8-way set associative)的含义是指,每个组里面有8个行。
我们知道,cache的容量要远远小于主存,主存和cache肯定不是一一对应的,那么主存中的地址和cache的映射关系是怎样的呢?
拿到一个地址,首先是映射到一个组里面去。如何映射?取内存地址的中间几位来映射。
举例来说,data cache: 32-KB, 8-way set associative, 64-byte line size
Cache总大小为32KB,8路组相连(每组有8个line),每个line的大小linesize为64Byte,OK,我们可以很轻易的算出一共有32K/8/64=64 个组。
对于32位的内存地址,每个line有2^6 = 64Byte,所以地址的【0,5】区分line中的那个字节。一共有64个组。我们取内存地址中间6为来hash查找地址属于那个组。即内存地址的【6,11】位来确定属于64组的哪一个组。组确定了之后,【12,31】的内存地址与组中8个line挨个比对,如果【12,31】为与某个line一致,并且这个line为有效,那么缓存命中。
OK,cache分成三类,
1 直接映射高速缓存,这个简单,即每个组只有一个line,选中组之后不需要和组中的每个line比对, 因为只有一个line。
2 组相联高速缓存,这个就是我们前面介绍的cache。 S个组,每个组E个line。
3 全相联高速缓存,这个简单,只有一个组,就是全相联。不用hash来确定组,直接挨个比对高位地址,来确定是否命中。可以想见这种方式不适合大的缓存。想想看,如果4M 的大缓存 linesize为32Byte,采用全相联的话,就意味着4*1024*1024/32 = 128K 个line挨个比较,来确定是否命中,这是多要命的事情。高速缓存立马成了低速缓存了。
描述一个cache需要以下参数 :
1 cache分级,L1 cache, L2 cache, L3 cache,级别越低,离cpu越近
2 cache的容量
3 cache的linesize
4 cache 每组的行个数.
组的个数完全可以根据上面的参数计算出来,所以没有列出来.
Intel手册中用这样的句子来描述cache:
8-MB L3 Cache, 16-way set associative, 64-byte line size
如何获取cache的参数呢,到了我们的老朋友cpuid指令,当eax为0x2的时候,cpuid指令获取到cache的参数. 下面给出代码:
- #include
- #include
- int d_eax;
- int d_ebx;
- int d_ecx;
- int d_edx;
- int parse_cache()
- {
- asm
- (
- "movl $2,%eax\n\t"
- "cpuid\n\t"
- "mov %eax,d_eax\n\t"
- "mov %ebx,d_ebx\n\t"
- "mov %ecx,d_ecx\n\t"
- "mov %edx,d_edx\n\t"
- );
- printf("d_eax : %x\nd_ebx : %x\nd_ecx : %x\nd_edx : %x\n",
- d_eax,d_ebx,d_ecx,d_edx);
- return 0;
- }
- int main()
- {
- parse_cache();
- return 0;
- }
- root@libin:~/program/assembly/cache# ./test
- d_eax : 55035a01
- d_ebx : f0b2dd
- d_ecx : 0
- d_edx : 9ca212c
我的电脑上运行结果如上图,查看intel的手册可知
- EAX
- (55h) Instruction TLB: 2-MB or 4-MB pages, fully associative, 7 entries
- (03h) Data TLB: 4-KB Pages, 4-way set associative, 64 entries
- (5Ah) Data TLB0: 2-MB or 4-MB pages, 4-way associative, 32 entries
- (01h) Instruction TLB: 4-KB Pages, 4-way set associative, 32 entries
- EBX:
- (F0h) 64-byte Prefetching
- (B2h) Instruction TLB: 4-KB pages, 4-way set associative, 64 entries
- (DDh) 3rd-level cache: 3-MB, 12-way set associative, 64-byte line size
- EDX:
- (09h) 1st-level Instruction Cache: 32-KB, 4-way set associative, 64-byte line size
- (CAh) Shared 2nd-level TLB: 4-KB pages, 4-way set associative, 512 entries
- (21h) 256KB L2 (MLC), 8-way set associative, 64-byte line size
- (2Ch) 1st-level data cache: 32-KB, 8-way set associative, 64-byte line size
参考文献:
1 Intel? Processor Identification andthe CPUID Instruction
2 Professional Assembly Language Richard Blum著
3 深入理解计算机系统
首先言明,本文严格意义上将不能算作原创,因为我写这些东西只不过是博客 Gallery of Processor Cache Effect的学习心得,不能将版权划到自己名下,毕竟咱不是喜欢45度角仰望天空的郭四姑娘。由于原文是英文版,而且作者用的是C++。原文提到的实验,我做了一部分,加深了对Cache的理解。英文比较好的兄弟就不必听我聒噪了,直接点链接看原文好了。
OK,继续我们的探索之旅。深入理解cache(1)得到了我的PC的cache参数如下:
L1 Cache : 32KB , 8路组相连,linesize为 64Byte 64个组
L2 Cache:256KB 8路组相连,linesize为 64Byte 512个组
L3 Cache: 3MB 12路组相连,linesize为 64Byte 4096个组
EAX(55h) Instruction TLB: 2-MB or 4-MB pages, fully associative, 7 entries(03h) Data TLB: 4-KB Pages, 4-way set associative, 64 entries(5Ah) Data TLB0: 2-MB or 4-MB pages, 4-way associative, 32 entries(01h) Instruction TLB: 4-KB Pages, 4-way set associative, 32 entriesEBX:(F0h) 64-byte Prefetching(B2h) Instruction TLB: 4-KB pages, 4-way set associative, 64 entries
(DDh) 3rd-level cache: 3-MB, 12-way set associative, 64-byte line sizeEDX:(09h) 1st-level Instruction Cache: 32-KB, 4-way set associative, 64-byte line size(CAh) Shared 2nd-level TLB: 4-KB pages, 4-way set associative, 512 entries
(21h) 256KB L2 (MLC), 8-way set associative, 64-byte line size
(2Ch) 1st-level data cache: 32-KB, 8-way set associative, 64-byte line size、
1 测试cache的linesize
代码看起来有点长,但是分成了3段。先看第一个测试,测试cache的linesize。
我们知道,cache的迁移是以linesize为单位的,所以,用户纵然只访问一个int,PC需要从主存拷贝1条line 进入Cache,对于我的电脑来说,就是copy 64B。
看下面的代码,测试linesize,如果K=1,遍历整个数组,如果K=16,只访问16倍数位置的值。依次类推。如果K=16,乘法的个数是K=1的时候1/16。我们可以推测,K=16的时候,程序执行时间是K=1的时候的1/16左右。是不是这样的。看下第一个测试用例的结果。
- int test_cache_linesize(int array[],int len,int K)
- {
- int i;
- for( i = 0;i<len;i += K)
- {
- array[i] *=3;
- }
- return 0;
- }
当K = 1 ,2,4 ......16的时候,虽然计算乘法的次数相差很大,但是,代码执行的时间是相近的都是80ms附近,但是当K = 32,64的时候,随着计算乘法的次数减半,代码执行的时间也减半。
原因在于,16 = (linesize)/sizeof(int)= 64/4,当K <16的时候,第一个int不命中,接下来的都命中的,乘法的个数虽然减半,但是从主存向Cache拷贝数据并没有减半。乘法消耗的指令周期要远低于从主存往cache里面copy数据,所以当K<16 的时候,既然从主存Cp数据到Cache的次数是相同的,那么总的执行时间差距不大就可以理解了。
当K>16的时候,每次都需要去主存取新的line,所以步长K增大一倍,去主存copy数据到cache的次数就减少为原来的一半,所以运行时间也减少为 原来的1半。
2 Cache的大小。
我的PC 有三级Cache,容量分别是32K 256K ,3M .这些参数对程序有什么影响呢。
下面的测试代码,执行的次数是一样的,都是64M次但是array的大小不一样。我们分别传入参数为1K,2K ,4K ,8K.....64MB 。在执行之前我们先分析下。
目前,如果array的大小是多大,循环执行的次数是一样的。我们的1级Cache大小是32KB,也就是最多容纳8192个int。如果我们的数组大小就是8192个int,那么除了第一次执行需要将数据从 主存-->L3 Cache--->L2 Cache -->L1 Cache传上来,后面再次执行的时候,由于整个数组全在L1 Cache,L1 Cache命中,速度很快。当然如果数组大小小于8192个int,L1更能容纳的下。8192是个坎。数组大于8192个int,性能就会下降一点。
如果我们的array大小大于L1 cache容量会怎样呢?看下我们的L2 Cache,大小256KB,即64K个int,换句话说,如果数组长度小于64K个int,也不赖,至少L2 Cache 容纳的下,虽然L1 Cache每写满32KB就需要将交换出去。换句话说,64K是个坎,数组大于64K个int,性能就会下降。
L3Cache我就不说,毕竟我不是唐僧,一样的情况,对于我的3M 缓存,3M/4 = 768K 是个坎,如果数组大于768个int,那么性能又会下降。
好了可以看下面的图了,和我们想的一样,
当低于8192的时候,都是120ms 左右,
[8192,64K ]的时候,都是200ms 左右
[64K ,768K ]的时候,都是300ms左右
大于768的时候,1200ms左右。
- int test_cache_capacity(int array[],int cap)
- {
- int i;
- int lenmod = cap -1;
- int times = 64*SIZE_1MB;
- for(i = 0;i<times;i++)
- {
- array[(i*16) & (lenmod)]++;/*16 means linesize/sizeof(int) = 16*/
- }
- return 0;
- }
第三部分我就不讲了,源代码给出大家可以自己在电脑上研究。不过第三部分要比较难懂,而且我前面提到的那篇讲的也不是很好懂。
下面是我的测试全代码
/* http://igoro.com/archive/gallery-of-processor-cache-effects/ */
#include <stdio .h >
#include <stdlib .h >
#include <linux /types .h >
#include < string .h >
#define SIZE_1KB (1024 )
#define SIZE_1MB (1024 *1024 )
#define NUMBER 64 *SIZE_1MB
#define MILLION 1000000
__u64 rdtsc ( )
{
__u32 hi ;
__u32 lo ;
__asm__ __volatile__
(
"rdtsc" : "=a" (lo ) , "=d" (hi )
) ;
return (__u64 )hi < <32 |lo ;
}
__u64 gettime ( )
{
struct timeval tv ;
gettimeofday ( &tv , NULL ) ;
return ( (__u64 ) (tv .tv_sec ) ) *MILLION +tv .tv_usec ;
}
int test_cache_linesize ( int array [ ] , int len , int K )
{
int i ;
for ( i = 0 ;i < len ;i + = K )
{
array [i ] * =3 ;
}
return 0 ;
}
int test_cache_capacity ( int array [ ] , int cap )
{
int i ;
int lenmod = cap -1 ;
int times = 64 *SIZE_1MB ;
for (i = 0 ;i <times ;i + + )
{
array [ (i *16 ) & (lenmod ) ] + + ; / *16 means linesize /sizeof ( int ) = 16 * /
}
return 0 ;
}
int test_cache_associative ( int array [ ] , int size , int K )
{
int i ;
int cur =0 ;
__u64 begin ;
__u64 end ;
begin =gettime ( ) ;
for ( i = 0 ;i <SIZE_1MB ;i + + )
{
array [cur ] + + ;
cur + = K ;
if (cur > = size )
cur = 0 ;
}
end = gettime ( ) ;
printf ( "when size = %10d, K = %10d : test_cache_associative cost %14llu us\n" ,
size ,K , end -begin ) ;
return 0 ;
}
int test_cache ( )
{
int * array = NULL ;
array = malloc (NUMBER *sizeof ( int ) ) ;
__u64 begin ;
__u64 end ;
int i ;
int K ;
int cap ;
int size ;
if ( array = = NULL )
{
printf ( "malloc space for array failed \n" ) ;
return -1 ;
}
for (i = 0 ;i <NUMBER ;i + + )
{
array [i ] = i ;
}
printf ( "---------test cache linesize-------------------------------------------\n" ) ;
for (K = 1 ;K < 64 *1024 ;K * = 2 )
{
begin = gettime ( ) ;
test_cache_linesize ( array ,NUMBER ,K ) ;
end = gettime ( ) ;
printf ( "when K = %10d,multiply %10d times,cost %14llu us,average cost %llu us\n" ,
K ,NUMBER /K , end - begin , ( end -begin ) / (NUMBER /K ) ) ;
if (K = = 1 )
{
begin = gettime ( ) ;
test_cache_linesize ( array ,NUMBER ,K ) ;
end = gettime ( ) ;
printf ( "when K = %10d,multiply %10d times,cost %14llu us,average cost %llu us\n" ,
K ,NUMBER /K , end - begin , ( end -begin ) / (NUMBER /K ) ) ;
}
}
printf ( "-----------test cache capacity-------------------------------------------\n" ) ;
for (cap = 1024 ;cap < = NUMBER ;cap * = 2 )
{
begin =gettime ( ) ;
test_cache_capacity ( array ,cap ) ;
end = gettime ( ) ;
printf ( "when cap = %10d,cost %14llu us\n" ,
cap , end -begin ) ;
if (cap = = 2 *SIZE_1MB /sizeof ( int ) )
{
begin =gettime ( ) ;
test_cache_capacity ( array ,3 *SIZE_1MB /sizeof ( int ) ) ;
end = gettime ( ) ;
printf ( "when cap = %10d,cost %14llu us\n" ,
3 *SIZE_1MB /sizeof ( int ) , end -begin ) ;
}
}
printf ( "-----------test cache associative ---------------------------------------\n" ) ;
for (size = 1 *SIZE_1MB ;size > = 4 *SIZE_1KB ;size / = 2 )
{
for (K = 64 ;K < = 576 ;K + = 64 )
{
test_cache_associative ( array ,size ,K ) ;
}
}
free ( array ) ;
return 0 ;
}
int main ( )
{
test_cache ( ) ;
return 0 ;
}
#include <stdio .h >
#include <stdlib .h >
#include <linux /types .h >
#include < string .h >
#define SIZE_1KB (1024 )
#define SIZE_1MB (1024 *1024 )
#define NUMBER 64 *SIZE_1MB
#define MILLION 1000000
__u64 rdtsc ( )
{
__u32 hi ;
__u32 lo ;
__asm__ __volatile__
(
"rdtsc" : "=a" (lo ) , "=d" (hi )
) ;
return (__u64 )hi < <32 |lo ;
}
__u64 gettime ( )
{
struct timeval tv ;
gettimeofday ( &tv , NULL ) ;
return ( (__u64 ) (tv .tv_sec ) ) *MILLION +tv .tv_usec ;
}
int test_cache_linesize ( int array [ ] , int len , int K )
{
int i ;
for ( i = 0 ;i < len ;i + = K )
{
array [i ] * =3 ;
}
return 0 ;
}
int test_cache_capacity ( int array [ ] , int cap )
{
int i ;
int lenmod = cap -1 ;
int times = 64 *SIZE_1MB ;
for (i = 0 ;i <times ;i + + )
{
array [ (i *16 ) & (lenmod ) ] + + ; / *16 means linesize /sizeof ( int ) = 16 * /
}
return 0 ;
}
int test_cache_associative ( int array [ ] , int size , int K )
{
int i ;
int cur =0 ;
__u64 begin ;
__u64 end ;
begin =gettime ( ) ;
for ( i = 0 ;i <SIZE_1MB ;i + + )
{
array [cur ] + + ;
cur + = K ;
if (cur > = size )
cur = 0 ;
}
end = gettime ( ) ;
printf ( "when size = %10d, K = %10d : test_cache_associative cost %14llu us\n" ,
size ,K , end -begin ) ;
return 0 ;
}
int test_cache ( )
{
int * array = NULL ;
array = malloc (NUMBER *sizeof ( int ) ) ;
__u64 begin ;
__u64 end ;
int i ;
int K ;
int cap ;
int size ;
if ( array = = NULL )
{
printf ( "malloc space for array failed \n" ) ;
return -1 ;
}
for (i = 0 ;i <NUMBER ;i + + )
{
array [i ] = i ;
}
printf ( "---------test cache linesize-------------------------------------------\n" ) ;
for (K = 1 ;K < 64 *1024 ;K * = 2 )
{
begin = gettime ( ) ;
test_cache_linesize ( array ,NUMBER ,K ) ;
end = gettime ( ) ;
printf ( "when K = %10d,multiply %10d times,cost %14llu us,average cost %llu us\n" ,
K ,NUMBER /K , end - begin , ( end -begin ) / (NUMBER /K ) ) ;
if (K = = 1 )
{
begin = gettime ( ) ;
test_cache_linesize ( array ,NUMBER ,K ) ;
end = gettime ( ) ;
printf ( "when K = %10d,multiply %10d times,cost %14llu us,average cost %llu us\n" ,
K ,NUMBER /K , end - begin , ( end -begin ) / (NUMBER /K ) ) ;
}
}
printf ( "-----------test cache capacity-------------------------------------------\n" ) ;
for (cap = 1024 ;cap < = NUMBER ;cap * = 2 )
{
begin =gettime ( ) ;
test_cache_capacity ( array ,cap ) ;
end = gettime ( ) ;
printf ( "when cap = %10d,cost %14llu us\n" ,
cap , end -begin ) ;
if (cap = = 2 *SIZE_1MB /sizeof ( int ) )
{
begin =gettime ( ) ;
test_cache_capacity ( array ,3 *SIZE_1MB /sizeof ( int ) ) ;
end = gettime ( ) ;
printf ( "when cap = %10d,cost %14llu us\n" ,
3 *SIZE_1MB /sizeof ( int ) , end -begin ) ;
}
}
printf ( "-----------test cache associative ---------------------------------------\n" ) ;
for (size = 1 *SIZE_1MB ;size > = 4 *SIZE_1KB ;size / = 2 )
{
for (K = 64 ;K < = 576 ;K + = 64 )
{
test_cache_associative ( array ,size ,K ) ;
}
}
free ( array ) ;
return 0 ;
}
int main ( )
{
test_cache ( ) ;
return 0 ;
}
出自:http://blog.chinaunix.net/uid-24774106-id-2777989.html