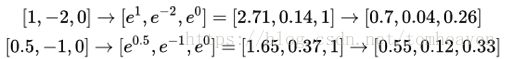再看Logistic回归与softmax函数

本专栏将推出一系列深度学习与图像处理相关的教程文章。注重原理精讲和代码实现。实现框架将重点选择Tensorflow或Pytorch。本讲讲解逻辑斯第回归的反向传播算法，重新审视softmax函数与sigmoid函数的联系。

---

逻辑斯第回归的反向传播算法

上一篇博文介绍了逻辑斯第回归：它是对二分类概率值的回归，用于分类。逻辑斯第回归可以重新形式化为：

P(y=0)=σ(wTx+b)(15) (15) P ( y = 0 ) = σ ( w T x + b )

其中 σ(t) σ ( t ) 为Sigmoid函数

σ(t)=11+exp(−t)(16) (16) σ ( t ) = 1 1 + exp ⁡ ( − t )

而 w∈Rm,b∈R w ∈ R m , b ∈ R 为待定模型参数。

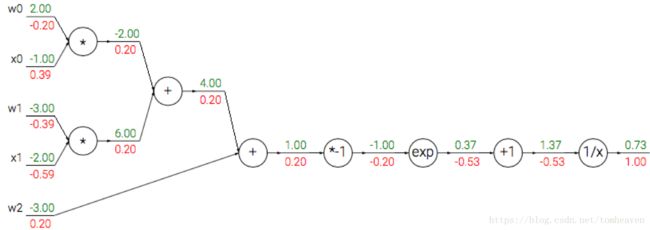
为了说明反向传播算法，我们需要实例化模型。不妨设 w=(−w0,−w1)T,w2=−b w = ( − w 0 , − w 1 ) T , w 2 = − b ，则

f(w,x)=11+exp(−wTx+b)=11+exp(−(w0x0+w1x1+w2))(17) (17) f ( w , x ) = 1 1 + exp ⁡ ( − w T x + b ) = 1 1 + exp ⁡ ( − ( w 0 x 0 + w 1 x 1 + w 2 ) )

函数 f(w,x) f ( w , x ) 可以看成四个基本函数的复合，因此计算梯度时可以用链式法则：

f(x)=1x fc(x)=c+x f(x)=exp(x) fa(x)=ax→∂f∂x=−1x2→∂f∂x=1→∂f∂x=exp(x)→∂f∂x=a(18) (18) f ( x ) = 1 x → ∂ f ∂ x = − 1 x 2   f c ( x ) = c + x → ∂ f ∂ x = 1   f ( x ) = exp ⁡ ( x ) → ∂ f ∂ x = exp ⁡ ( x )   f a ( x ) = a x → ∂ f ∂ x = a

在现代机器学习框架Tensorflow、Pytorch等的现实中，模型被构建为一个计算图（Computation Graph）。正向推理是按计算图正向计算（图中绿色）。反向传播则是按计算图反向计算梯度（图中红色），传播误差，更新权重。反向计算梯度这一过程也可以视为求导链式法则的应用。

图1 逻辑斯第回归的计算图（摘自cs231课件）

计算图可以拓展到更多层、复杂的模型中，从而称为机器学习模型的一般形式。

softmax函数与sigmoid函数的联系

逻辑斯第回归可以解决二分类问题，但是应用场景中更多的是多分类问题。如果问题推广到 n n -分类问题，那么我们希望模型的形式与逻辑斯第模型相似，为

o=f(Wx+b)(12) (12) o = f ( W x + b )

其中 W∈Rm×n，b∈Rn W ∈ R m × n ， b ∈ R n 为待定参数。 o∈Rn o ∈ R n 为one-hot 向量，它的哪个维度最大就表示特征 x x 代表的样本属于哪个类别。那么问题的关键就在于：函数 f f 如何定义？

这就引入了Softmax分类。Softmax分类就是逻辑斯蒂回归到多分类问题的推广，其概率预测模型定义为

ŷ =softmax(Wx+b)(13) (13) y ^ = softmax ( W x + b )

其中 ŷ ∈Rn y ^ ∈ R n 的第 c c 个元素 [ŷ ]c [ y ^ ] c 表示数据 x x 属于第 c c 个类别的概率。

而 softmax(z) softmax ( z ) 的第 c c 个元素定义为

[softmax(z)]c=exp([z]c)∑nk=1exp([z]k)(14) (14) [ softmax ( z ) ] c = exp ⁡ ( [ z ] c ) ∑ k = 1 n exp ⁡ ( [ z ] k )

图2展示了softmax函数处理两个三维向量的结果。可以看出softmax函数具有非极大值抑制的效果。也就是说这个函数能在模型训练中突出正确类别，并将正确类别的影响放大，从而加速模型的训练和收敛过程。

图2 向量经过softmax函数后的结果

softmax函数本质上通过 exp(⋅) exp ⁡ ( ⋅ ) 在模型中引入非线性特性，并且将预测值归一化，从而可以直接对应到类别概率。从这一点上看，softmax函数与sigmoid函数是非常类似的。

本文的实现代码已经在前一篇博文《逻辑斯第回归、softmax分类与多层感知器》中给出。