移动平均法(Moving average,MA) 指数平滑法(Exponential Smoothing,ES)
____tz_zs
注:本博客中关于概念的解释部分均来自 MBA智库百科
一、移动平均法(Moving average,MA)
移动平均法又称滑动平均法、滑动平均模型法
移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。移动平均法根据预测时使用的各元素的权重不同,可以分为:简单移动平均和加权移动平均。
移动平均法是一种简单平滑预测技术,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。
(一)简单移动平均法
简单移动平均的各元素的权重都相等。简单的移动平均的计算公式如下:
Ft=(At-1+At-2+At-3+…+At-n)/n
式中,
Ft--对下一期的预测值;
n--移动平均的时期个数;
At-1--前期实际值;
At-2,At-3和At-n分别表示前两期、前三期直至前n期的实际值。
小Demo
.
import matplotlib.pyplot as plt
# 简单移动平均法
def ma(list2):
n = len(list2)
sum = 0
for i in list2:
sum += i
result = sum / n
return result
def answer1(list1, n):
# 简单移动平均法
listMA = [] # 简单移动平均值的列表
for i in range(n - 1, len(list1)):
# print(i)
list2 = (list1[i - (n - 1):i + 1])
listMA.append(ma(list2))
print("简单移动平均值的列表:{}".format(listMA))
# 最后的移动平均值可做为下一个数的预测
x = listMA[-1]
print("下一个数的预测:{}".format(x))
# 画图
plt.scatter(list(range(len(listMA))), listMA)
plt.show()
if __name__ == '__main__':
list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13个
n = 3 # 移动平均期数
answer1(list1, n) # 简单移动平均法
.
运行结果:
.
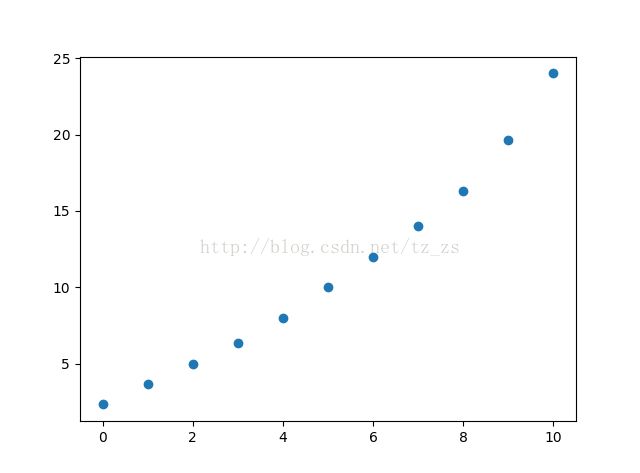
简单移动平均值的列表:[2.3333333333333335, 3.6666666666666665, 5.0, 6.333333333333333, 8.0, 10.0, 12.0, 14.0, 16.333333333333332, 19.666666666666668, 24.0]
下一个数的预测:24.0.
简单移动平均值散点图:
(二)加权移动平均法
加权移动平均给固定跨越期限内的每个变量值以不同的权重。其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以n为周期的周期性变化外,远离目标期的变量值的影响力相对较低,故应给予较低的权重。 加权移动平均法的计算公式如下:
Ft=w1At-1+w2At-2+w3At-3+…+wnAt-n
式中,
w1--第t-1期实际销售额的权重;
w2--第t-2期实际销售额的权重;
wn--第t-n期实际销售额的权重;
n--预测的时期数;w1+ w2+…+ wn=1
在运用加权平均法时,权重的选择是一个应该注意的问题。经验法和试算法是选择权重的最简单的方法。一般而言,最近期的数据最能预示未来的情况,因而权重应大些。例如,根据前一个月的利润和生产能力比起根据前几个月能更好的估测下个月的利润和生产能力。但是,如果数据是季节性的,则权重也应是季节性的。
小Demo
.
import matplotlib.pyplot as plt
# 加权移动平均法
def wma(list2, w):
n = len(list2)
sum = 0
for i in n:
sum += list2[i] * w[i]
return sum
def answer2(list1, n):
# 加权移动平均法
w = [0.2, 0.3, 0.5] # 各期的权重
listWMA = [] # 加权移动平均值的列表
for i in range(n - 1, len(list1)):
# print(i)
list2 = (list1[i - (n - 1):i + 1])
listWMA.append(ma(list2))
print("加权移动平均值的列表:{}".format(listWMA))
# 最后的移动平均值可做为下一个数的预测
x = listWMA[-1]
print("下一个数的预测:{}".format(x))
# 画图
plt.scatter(list(range(len(listWMA))), listWMA)
plt.show()
if __name__ == '__main__':
list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13个
n = 3 # 移动平均期数
answer2(list1, n) # 加权移动平均法运行结果:
.
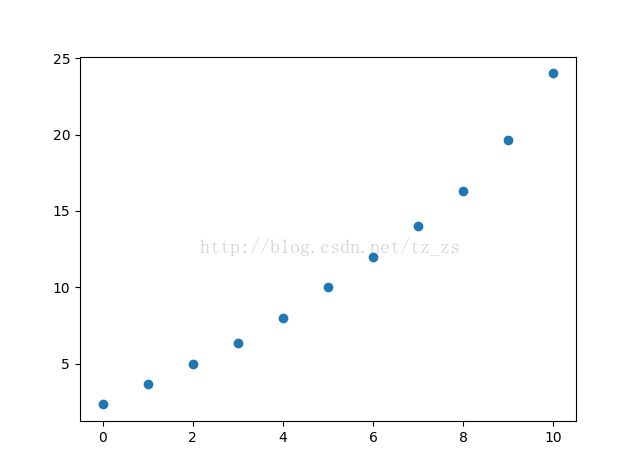
加权移动平均值的列表:[2.3333333333333335, 3.6666666666666665, 5.0, 6.333333333333333, 8.0, 10.0, 12.0, 14.0, 16.333333333333332, 19.666666666666668, 24.0]
下一个数的预测:24.0.
加权移动平均值散点图:
.
(三)移动平均法的优缺点
使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下问题:
1、 加大移动平均法的期数(即加大n值)会使平滑波动效果更好,但会使预测值对数据实际变动更不敏感;
2、 移动平均值并不能总是很好地反映出趋势。由于是平均值,预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动;
3、 移动平均法要由大量的过去数据的记录。
二、指数平滑法(Exponential Smoothing,ES)
指数平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较大的权数放在最近的资料。
指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
(一)指数平滑法的基本公式
S_t=a\cdot y_t+(1-a)S_{t-1}由该公式可知:式中,
St--时间t的平滑值;
yt--时间t的实际值;
St − 1--时间t-1的平滑值;
a--平滑常数,其取值范围为[0,1];
1.St是yt和 St − 1的加权算数平均数,随着a取值的大小变化,决定yt和 St − 1对St的影响程度,当a取1时,St = yt;当a取0时,St = St − 1。
2.St具有逐期追溯性质,可探源至St − t + 1为止,包括全部数据。其过程中,平滑常数以指数形式递减,故称之为指数平滑法。指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1,远期实际值对本期平滑值影响程度的下降越迅速;平滑常数a越接近于 0,远期实际值对本期平滑值影响程度的下降越缓慢。由此,当时间数列相对平稳时,可取较大的a;当时间数列波动较大时,应取较小的a,以不忽略远期实际值的影响。生产预测中,平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。
3.尽管St包含有全期数据的影响,但实际计算时,仅需要两个数值,即yt和 St − 1,再加上一个常数a,这就使指数滑动平均具逐期递推性质,从而给预测带来了极大的方便。
4.根据公式S_1=a\cdot y_1+(1-a)S_0,当欲用指数平滑法时才开始收集数据,则不存在y0。无从产生S0,自然无法据指数平滑公式求出S1,指数平滑法定义S1为初始值。初始值的确定也是指数平滑过程的一个重要条件。
如果能够找到y1以前的历史资料,那么,初始值S1的确定是不成问题的。数据较少时可用全期平均、移动平均法;数据较多时,可用最小二乘法。但不能使用指数平滑法本身确定初始值,因为数据必会枯竭。
如果仅有从y1开始的数据,那么确定初始值的方法有:
1)取S1等于y1;
2)待积累若干数据后,取S1等于前面若干数据的简单算术平均数,如:S1=(y1+ y2+y3)/3等等。
(二)指数平滑的预测公式
据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
(1) 一次指数平滑预测
当时间数列无明显的趋势变化,可用一次指数平滑预测。其预测公式为:
yt+1'=ayt+(1-a)yt'
式中,
yt+1'--t+1期的预测值,即本期(t期)的平滑值St ;
yt--t期的实际值;
yt'--t期的预测值,即上期的平滑值St-1 。
该公式又可以写作:yt+1'=yt'+a(yt- yt')。可见,下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。
(2) 二次指数平滑预测
二次指数平滑是对一次指数平滑的再平滑。它适用于具线性趋势的时间数列。其预测公式为:yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)
显然,二次指数平滑是一直线方程,其截距为:(2yt'-yt),斜率为:(yt'-yt) a/(1-a),自变量为预测天数。式中,
yt= ayt-1'+(1-a)yt-1
(3) 三次指数平滑预测
三次指数平滑预测是二次平滑基础上的再平滑。其预测公式是:
yt+m=(3yt'-3yt+yt)+[(6-5a)yt'-(10-8a)yt+(4-3a)yt]*am/2(1-a)2+ (yt'-2yt+yt')*a2m2/2(1-a)2
式中,
yt=ayt-1+(1-a)yt-1
它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
(三)指数平滑法的趋势调整
一段时间内收集到的数据所呈现的上升或下降趋势将导致指数预测滞后于实际需求。通过趋势调整,添加趋势修正值,可以在一定程度上改进指数平滑预测结果。调整后的指数平滑法的公式为:
包含趋势预测(YITt)=新预测(Yt)+趋势校正(Tt)
进行趋势调整的指数平滑预测有三个步骤:
1、 利用前面介绍的方法计算第t期的简单指数平滑预测(Yt);
2、 计算趋势。其公式为: Tt=(1-b)Tt-1+b(Yt-Yt-1)其中,
Tt=第t期经过平滑的趋势;
Tt-1=第t期上期经过平滑的趋势;
b=选择的趋势平滑系数;
Yt=对第t期简单指数平滑预测;
Yt-1=对第t期上期简单指数平滑预测。
3、计算趋势调整后的指数平滑预测值(YITt)。计算公式为:YITt=Yt+Tt。
.
import matplotlib.pyplot as plt
# 一次指数平滑预测
def es1(list3, t, a):
if t == 0:
return list3[0] # 初始的平滑值取实际值
return a * list3[t - 1] + (1 - a) * es1(list3, t - 1, a) # 递归调用 t-1 → 12
# 二次指数平滑预测
def es2(list3, t, a):
if t == 0:
return list3[0]
return (a * es2(list3, t - 1, a) + (1 - a) * list3[t - 1])
def answer3(list2):
# 指数平滑法
a = 0.8 # 平滑常数
listES = [] # 指数平滑值的列表
for i in range(len(list2)):
if i == 0:
listES.append(list2[i])
continue
s = a * list2[i] + (1 - a) * listES[-1]
listES.append(s)
print("指数平滑值的列表:{}".format(listES))
# 画图
plt.scatter(list(range(len(listES))), listES)
plt.show()
# 一次指数平滑预测
t = len(list2) # 预测的时期 13
x = es1(list2, t, a)
print("下一个数的一次指数平滑预测:{}".format(x))
# 二次指数平滑预测
m = 3 # 预测的值为之后的第m个
yt = es2(list2, t - 1, a)
ytm = listES[t - 2]
esm = ((2 * ytm - yt) + m * (ytm - yt) * a / (1 - a))
print("之后的第{}个数的二次指数平滑预测:{}".format(m, esm))
if __name__ == '__main__':
list1 = [1, 2, 4, 5, 6, 8, 10, 12, 14, 16, 19, 24, 29] # 13个
n = 3 # 移动平均期数
answer3(list1) # 指数平滑法
运行结果:
.
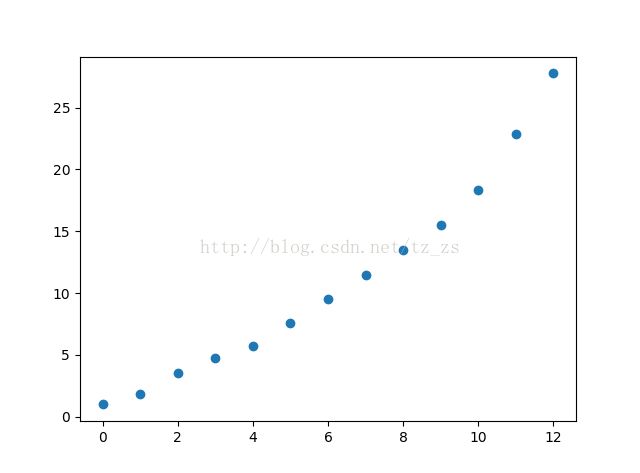
指数平滑值的列表:[1, 1.8, 3.56, 4.712, 5.742400000000001, 7.5484800000000005, 9.509696, 11.5019392, 13.50038784, 15.500077568, 18.300015513600002, 22.860003102720004, 27.772000620544002]
下一个数的一次指数平滑预测:27.772000620544002
之后的第3个数的二次指数平滑预测:137.5839514214401.
指数平滑值的散点图:
.