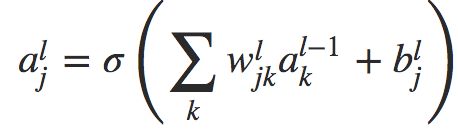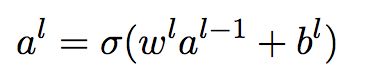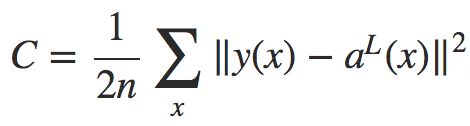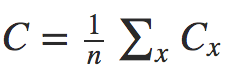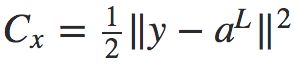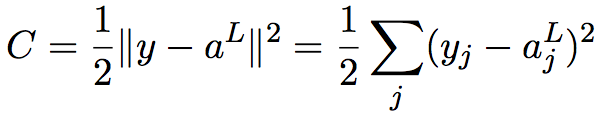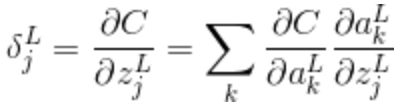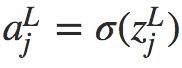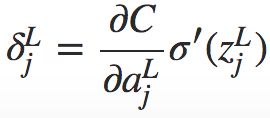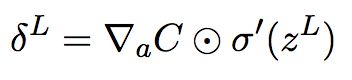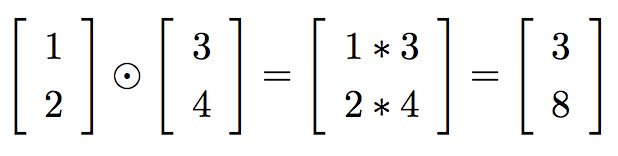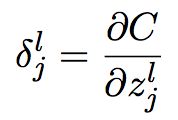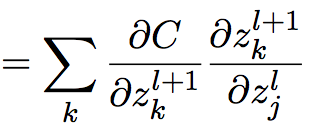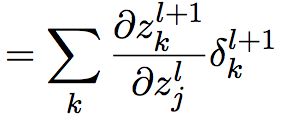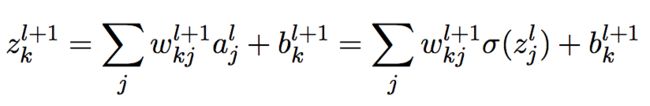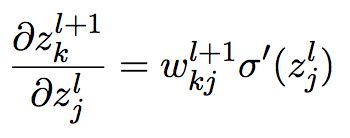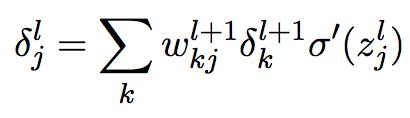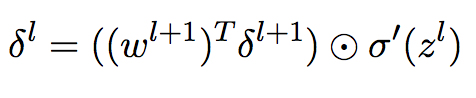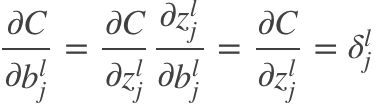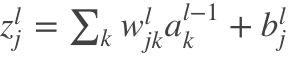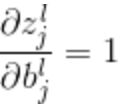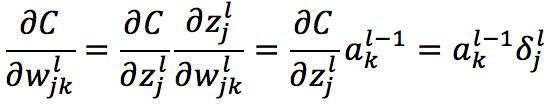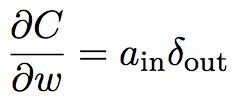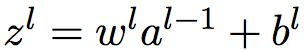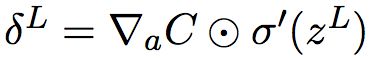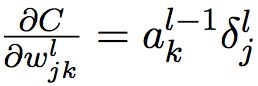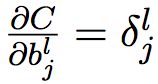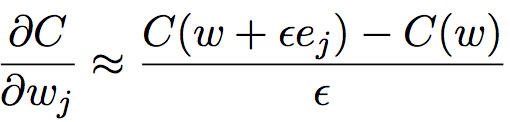神经网络的前向传播和反向传播
本博客是对Michael Nielsen所著的《Neural Network and Deep Learning》第2章内容的解读,有兴趣的朋友可以直接阅读原文http://neuralnetworksanddeeplearning.com/chap2.html
前向传播过程
在讨论反向传播之前,我们讨论一下前向传播,即根据输入X来计算输出Y。输入X用矩阵表示,我们看一下如何基于矩阵X来计算网络的输出Y。
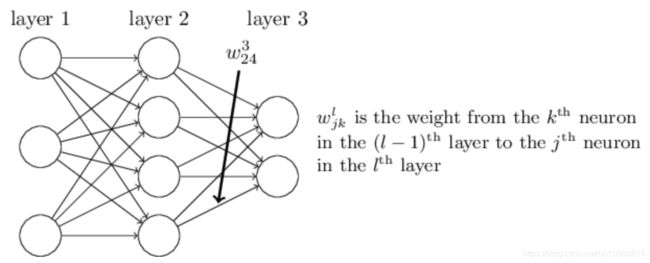
我们使用 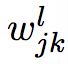 表示从 (
表示从 (![]() - 1) 层的第 k 个神经元到
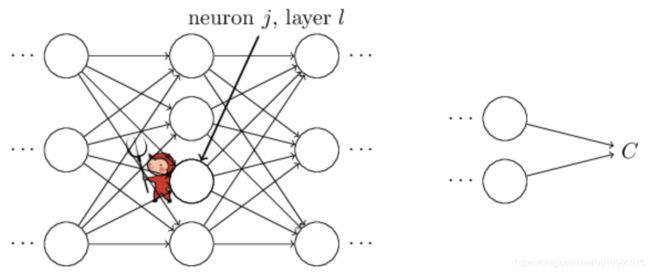
- 1) 层的第 k 个神经元到 ![]() 层的第 j 个神经元的链接上的权重。例如,下图给出了网络中第二层的第四个神经元到第三层的第二个神经元的链接上的权重:
层的第 j 个神经元的链接上的权重。例如,下图给出了网络中第二层的第四个神经元到第三层的第二个神经元的链接上的权重:
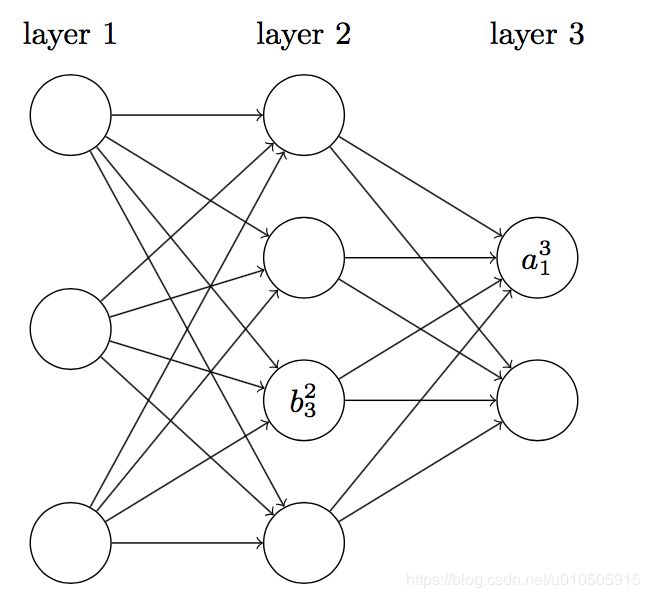
我们使用![]() 表示在
表示在 ![]() 层第 j 个神经元的偏置,使用
层第 j 个神经元的偏置,使用![]() 表示
表示 ![]() 层第 j 个神经元的激活值(激活函数的输出)。
层第 j 个神经元的激活值(激活函数的输出)。
对每一层 ![]() ,定义一个权重矩阵
,定义一个权重矩阵![]() ,权重矩阵
,权重矩阵 ![]() 的元素正是连接到
的元素正是连接到 ![]() 层神经元的权重,矩阵中第 j 行第 k 列的元素是
层神经元的权重,矩阵中第 j 行第 k 列的元素是 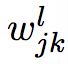 。类似的,对每一层
。类似的,对每一层![]() ,定义一个偏置向量
,定义一个偏置向量![]() ,向量的每个元素为
,向量的每个元素为![]() ,每个元素对应于
,每个元素对应于 ![]() 层每个神经元的偏置。最后,我们定义激活向量
层每个神经元的偏置。最后,我们定义激活向量![]() ,其元素是那些激活值
,其元素是那些激活值![]() 。
。
那么,公式(1)就可以表示为如下的向量形式:
这个表达式给出了一种更加全局的思考每层的激活值和前一层激活值的关联方式:用权重矩阵作用在激活值上,然后加上一个偏置向量,最后作用 σ 函数,则得到每层的激活值。
为了方便表示,记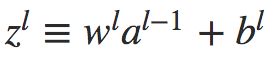 ,表示
,表示 ![]() 层神经元的权重输入,则公式(2)变为
层神经元的权重输入,则公式(2)变为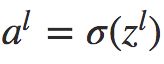 。
。
输入X,然后根据公式(2)一层层计算网络的激活值,最终得到网络的输出Y。
反向传播过程
反向传播的两个假设
反向传播的目标是计算代价函数C关于w和b的偏导数∂C/∂w 和 ∂C/∂b。为了使反向传播工作,我们需要对代价函数做两个假设。在给出这两个假设之前,我们先看一个具体的代价函数,即如下的二次代价函数:
其中x为训练样本,n是训练样本的总数;y = y(x) 是期望的输出,即样本的真实值;L表示网络的层数;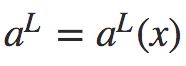 为网络的输出向量。
为网络的输出向量。
假设1:代价函数可以表示为单个样本的代价函数的均值,即:
需要做这个假设的原因是,反向传播实际上是对一个独立的训练样本计算了 ∂Cx/∂w 和 ∂Cx/∂b。在这个假设下,我们可以通过计算所有样本的平均来得到总体的∂C/∂w 和 ∂C/∂b。
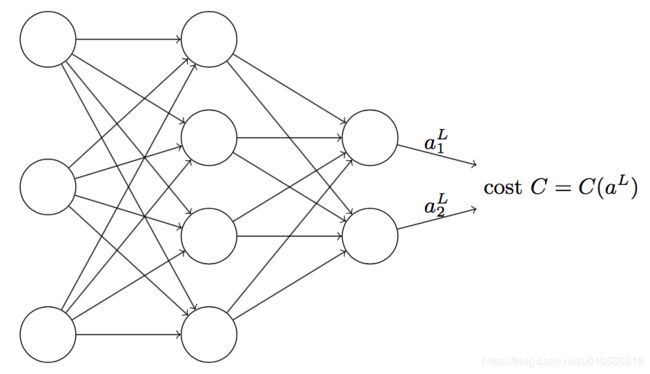
假设2:代价函数可以表示为神经网络输出的函数:
比如,单个样本x的平方代价函数可以写为:
这是输出的激活值的函数。当然,这个代价函数同样还依赖于目标输出 y。不过,输入的训练样本 x 是固定的,所以输出 y 同样是一个固定的参数。尤其是它并不会随权重和偏置而改变,也就是说,这不是神经网络学习的对象。所以,将C看成输出激活值![]() 的函数才是合理的,而 y 仅仅是帮助定义函数的参数而已。
的函数才是合理的,而 y 仅仅是帮助定义函数的参数而已。
反向传播的四个基本方程
反向传播指的是权重w和偏置b的改变如何改变代价函数C。其含义其实就是计算偏导数 和
和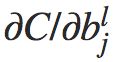 。在讨论基本方程之前,我们引入一个中间变量
。在讨论基本方程之前,我们引入一个中间变量![]() ,表示第
,表示第 ![]() 层第 j 个单元的误差。关于误差,《Neural Networks and Deep Learning》给出了一个很形象的例子:
层第 j 个单元的误差。关于误差,《Neural Networks and Deep Learning》给出了一个很形象的例子:
如上图所示,假设网络中有个小调皮鬼,他在第 ![]() 层第 j 个神经元上。当输入进来时,调皮鬼对神经元的操作进行扰乱,导致神经元的权重输入增加很小的变化
层第 j 个神经元上。当输入进来时,调皮鬼对神经元的操作进行扰乱,导致神经元的权重输入增加很小的变化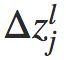 ,使得神经元输出由
,使得神经元输出由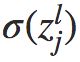 变为
变为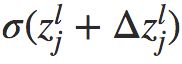 。这个变化向网络后面的层进行传播,最终导致整个代价产生的改变为
。这个变化向网络后面的层进行传播,最终导致整个代价产生的改变为 。
。
现在,这个调皮鬼改过自新了,他想帮助我们尽可能减小代价,他试着找到可以让代价更小的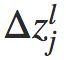 。假设
。假设 一开始是个很大的正值或负值,那么,调皮鬼可以通过选择一个和
一开始是个很大的正值或负值,那么,调皮鬼可以通过选择一个和 方向相反的
方向相反的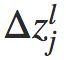 使代价函数更小。随着迭代的进行,
使代价函数更小。随着迭代的进行, 会逐渐趋近于0,那么
会逐渐趋近于0,那么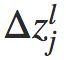 对代价函数的改进就微乎其微了。这时,对调皮鬼来说,他已经找到最优解了(局部最优)。这启发我们可以用
对代价函数的改进就微乎其微了。这时,对调皮鬼来说,他已经找到最优解了(局部最优)。这启发我们可以用 来衡量神经元的误差。即,
来衡量神经元的误差。即,![]() 层第 j 个神经元的误差
层第 j 个神经元的误差![]() 为:
为:
下面我们看看反向传播的四个基本方程。
由于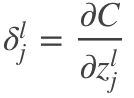 ,应用链式法则,加入输出激活值的偏导数,则之前偏导数变为:
,应用链式法则,加入输出激活值的偏导数,则之前偏导数变为:
求和是在输出层的所有神经元k上进行的。第 k 个神经元的输出激活值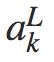 只依赖于当 k = j 时第 j 个神经元的输入权重
只依赖于当 k = j 时第 j 个神经元的输入权重![]() ,所以当 k ≠ j 时
,所以当 k ≠ j 时 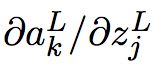 项为0。则上一个方程可以简化为:
项为0。则上一个方程可以简化为:
右式第一项∂C/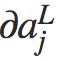 表示代价随着第 j 个输出激活值的变化而变化的速度。右式第二项
表示代价随着第 j 个输出激活值的变化而变化的速度。右式第二项 刻画了在
刻画了在![]() 处激活函数 σ 变化的速度。
处激活函数 σ 变化的速度。
(BP1)改写为矩阵形式,为:
其中,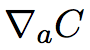 是一个向量,其元素为偏导数∂C/
是一个向量,其元素为偏导数∂C/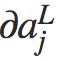 。
。![]() 表示hadamard乘积运算。
表示hadamard乘积运算。
注:hadamard乘积即按元素乘法,比如:
2. 误差传递方程:
注意:
做微分,则得到:
把它代入公式(9),则得到:
改为分量形式,则为:
这个方程说明我们可以通过第 l + 1 层的误差![]() 计算第 l 层的误差
计算第 l 层的误差![]() 。结合(BP1)和(BP2),我们可以计算任何层的误差
。结合(BP1)和(BP2),我们可以计算任何层的误差![]() 。首先,使用方程(BP1)计算
。首先,使用方程(BP1)计算![]() ,然后用方程(BP2)来计算
,然后用方程(BP2)来计算![]() ,然后再次用方程(BP2)来计算
,然后再次用方程(BP2)来计算![]() ,如此一步一步的反向传播完整个网络。
,如此一步一步的反向传播完整个网络。
3. 代价函数对bias的改变率
4. 代价函数对权重的改变率
可以简写为:
其中,![]() 是输入给权重w的的神经元的激活值,
是输入给权重w的的神经元的激活值,![]() 是输出自权重 w 的神经元的误差。
是输出自权重 w 的神经元的误差。
不难看出,当上一层激活值很小的时候,即![]() ≈ 0,无论误差多大,梯度 ∂C/∂w 也会很小,表示在梯度下降的时候,这个权重不会改变太多。也就是说,来自低激活值神经元的权重学习会非常缓慢。
≈ 0,无论误差多大,梯度 ∂C/∂w 也会很小,表示在梯度下降的时候,这个权重不会改变太多。也就是说,来自低激活值神经元的权重学习会非常缓慢。
另外,从输出层看,先看看(BP1 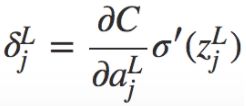 )中的项
)中的项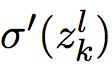 。若σ为sigmoid函数,在靠近0和1的时候,σ函数变得非常平。这时
。若σ为sigmoid函数,在靠近0和1的时候,σ函数变得非常平。这时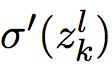 ≈ 0。所以,如果输出神经元处于低激活值(≈ 0)或高激活值(≈ 1)时,最终层的权重/bias变化也会比较小,学习变慢。此时,我们常常称输出神经元已经饱和了。
≈ 0。所以,如果输出神经元处于低激活值(≈ 0)或高激活值(≈ 1)时,最终层的权重/bias变化也会比较小,学习变慢。此时,我们常常称输出神经元已经饱和了。
总结来说,如果输入神经元激活值很低,或者输出神经元已经饱和了(过高或过低的激活值),权重和bias会学习的非常慢。
反向传播算法
有了以上反向传播方程,反向传播算法描述如下:
1. 输出 x
4. 反向传播误差:对每个 l = L - 1, L - 2, ..., 2,计算
得到梯度后,就可以使用梯度下降法对参数进行一轮轮更新了,直到最后模型收敛。
为什么说反向传播算法高效
在哪种层面上,反向传播是快速的算法?为了回答这个问题,首先考虑另一个计算梯度的方法。把代价看做权重的函数 C = C(w)。你给这些权重![]() ,...进行编号,期望计算某些权重
,...进行编号,期望计算某些权重![]() 的偏导数
的偏导数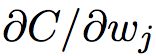 。 而一种近似的方法就是下面这种:
。 而一种近似的方法就是下面这种:
其中 ε > 0 是一个很小的正数,而 ![]() 是在第 j 个方向上的单位向量。换句话说,我们可以通过计算两个接近相同的
是在第 j 个方向上的单位向量。换句话说,我们可以通过计算两个接近相同的 ![]() 的代价 C 来估计
的代价 C 来估计 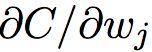 。同样方法也可以用来计算 ∂C/∂b。
。同样方法也可以用来计算 ∂C/∂b。
不过,这个方法非常低效。假如我们的网络中有100万个权重。要计算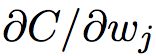 ,我们需要从头到尾进行一次完整的前向传播才能得到
,我们需要从头到尾进行一次完整的前向传播才能得到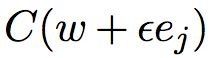 的值。要计算100万个权重的偏导就需要前向传播100万次。我们同样需要计算 C(w),需要一次网络传播。总共需要 100百万+1 次网络传播。
的值。要计算100万个权重的偏导就需要前向传播100万次。我们同样需要计算 C(w),需要一次网络传播。总共需要 100百万+1 次网络传播。
再反观反向传播算法,根据方程(BP4),我们只需要知道 和
和![]() 就能计算出
就能计算出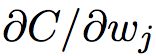 。激活值
。激活值 在一次前向传播后就能全部得到,然后利用(BP1)和(BP2)就可以计算出
在一次前向传播后就能全部得到,然后利用(BP1)和(BP2)就可以计算出![]() 。反向传播和前向传播计算量相当,所以,总共需要2次前向传播的计算量就能计算出所有的
。反向传播和前向传播计算量相当,所以,总共需要2次前向传播的计算量就能计算出所有的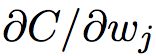 。对比用微分定义求偏导的100百万次,计算量大大减少。
。对比用微分定义求偏导的100百万次,计算量大大减少。