轻松理解skip-gram模型

引言

在许多自然语言处理任务中，许多单词表达是由他们的tf-idf分数决定的。即使这些分数告诉我们一个单词在一个文本中的相对重要性，但是他们并没有告诉我们单词的语义。Word2vec是一类神经网络模型——在给定无标签的语料库的情况下，为语料库中的单词产生一个能表达语义的向量。这些向量通常是有用的：

• 通过词向量来计算两个单词的语义相似性
• 对某些监督型NLP任务如文本分类，语义分析构造特征

接下来我将描述Word2vec其中一个模型，叫做skip-gram模型

skip-gram模型

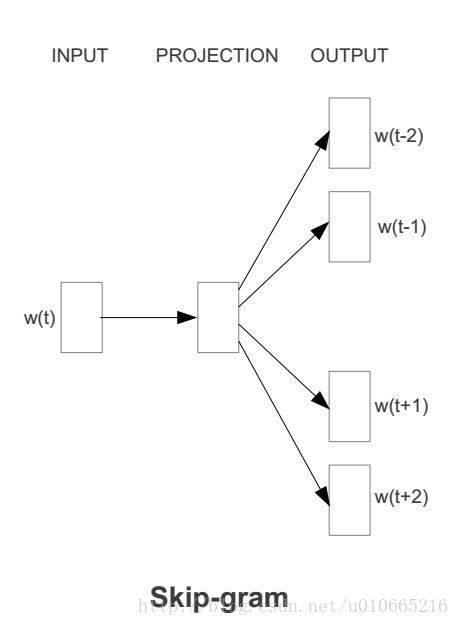
在我详细介绍skip-gram模型前，我们先来了解下训练数据的格式。skip-gram模型的输入是一个单词 wI ，它的输出是 wI 的上下文 wO,1,...,wO,C ，上下文的窗口大小为 C 。举个例子，这里有个句子“I drive my car to the store”。我们如果把”car”作为训练输入数据，单词组{“I”, “drive”, “my”, “to”, “the”, “store”}就是输出。所有这些单词，我们会进行one-hot编码。skip-gram模型图如下所示：

前向传播

接下来我们来看下skip-gram神经网络模型，skip-gram的神经网络模型是从前馈神经网络模型改进而来，说白了就是在前馈神经网络模型的基础上，通过一些技巧使得模型更有效。我们先上图，看一波skip-gram的神经网络模型：

在上图中，输入向量 x 代表某个单词的one-hot编码，对应的输出向量{ y1 ,…, yC }。输入层与隐藏层之间的权重矩阵 W 的第 i 行代表词汇表中第 i 个单词的权重。接下来重点来了：这个权重矩阵 W 就是我们需要学习的目标（同 W′ ），因为这个权重矩阵包含了词汇表中所有单词的权重信息。上述模型中，每个输出单词向量也有个 N×V 维的输出向量 W′ 。最后模型还有 N 个结点的隐藏层，我们可以发现隐藏层节点 hi 的输入就是输入层输入的加权求和。因此由于输入向量 x 是one-hot编码，那么只有向量中的非零元素才能对隐藏层产生输入。因此对于输入向量 x 其中 xk=1 并且 xk′=0,k≠k′ 。所以隐藏层的输出只与权重矩阵第 k 行相关，从数学上证明如下：

h=xTW=Wk,.:=vwI(1)

注意因为输入时one-hot编码，所以这里是不需要使用激活函数的。同理，模型输出结点 C×V 的输入也是由对应输入结点的加权求和计算得到：

uc,j=v′Twjh(2)

其实从上图我们也看到了输出层中的每个单词都是共享权重的，因此我们有 uc,j=uj 。最终我们通过softmax函数产生第 C 个单词的多项式分布。

p(wc,j=wO,c|wI)=yc,j=exp(uc,j)∑Vj′=1exp(uj′)(3)

说白了，这个值就是第C个输出单词的第j个结点的概率大小。

通过BP（反向传播）算法及随机梯度下降来学习权重

前面我讲解了skip-gram模型的输入向量及输出的概率表达，以及我们学习的目标。接下来我们详细讲解下学习权重的过程。第一步就是定义损失函数，这个损失函数就是输出单词组的条件概率，一般都是取对数，如下所示：

E=−logp(wO,1,wO,2,...,wO,C|wI)(4)

=−log∏c=1Cexp(uc,j)∑Vj′=1exp(u′j)(5)

接下来就是对上面的概率求导，具体推导过程可以去看BP算法，我们得到输出权重矩阵 W′ 的更新规则：

w′(new)=w′(old)ij−η⋅∑c=1C(yc,j−tc,j)⋅hi(6)

同理权重 W 的更新规则如下：

w(new)=w(old)ij−η⋅∑j=1V∑c=1C(yc,j−tc,j)⋅w′ij⋅xj(7)

从上面的更新规则，我们可以发现，每次更新都需要对整个词汇表求和，因此对于很大的语料库来说，这个计算复杂度是很高的。于是在实际应用中，Google的Mikolov等人提出了分层softmax及负采样可以使得计算复杂度降低很多。

参考文献

[1] Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.（这篇文章就讲了两个模型：CBOW 和 Skip-gram）
[2] Mikolov T, Sutskever I, Chen K, et al. Distributed Representations of Words and Phrases and their Compositionality[J]. 2013, 26:3111-3119.（这篇文章针对Skip-gram模型计算复杂度高的问题提出了一些该进）
[3] Presentation on Word2Vec（这是NIPS 2013workshop上Mikolov的PPT报告）