【机器学习基础】EM算法
目录
一 样例
二 公式描述
三 参考文献
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
最大期望算法经过两个步骤交替进行计算:
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
一 样例
举个例子,抛硬币,有两个硬币,但是两个硬币的材质不同导致其出现正反面的概率不一样,目前我们只有一组观测数据,要求出每一种硬币投掷时正面向上的概率。总共投了五轮,每轮投掷五次,现在先考虑一种简单的情况,假设我们知道这每一轮用的是哪一个硬币去投掷的:
![]()
那么我们拿着这样的一组数据,就可以很轻松的估计出A硬币和B硬币出现正面的概率,如下:
PA = (3+1+2)/ 15 = 0.4
PB= (2+3)/10 = 0.5
现在把问题变得复杂一点,假设我们不知道每一次投掷用的是哪一种硬币,等于是现在的问题加上了一个隐变量,就是每一次选取的硬币的种类。
那么现在可以想一想,假设我们把每一次硬币的种类设为z,则这五次实验生成了一个5维的向量(z1,z2,z3,z4,z5),现在问题来了,如果我们要根据观测结果去求出PA,PB,那么首先需要知道z,但是如果用最大似然估计去估计z,又要先求出PA,PB。这就产生了一个循环。那么这个时候EM算法的作用就体现出来了,EM算法的基本思想是:先初始化一个PA,PB,然后我们拿着这个初始化的PA,PB用最大似然概率估计出z,接下来有了z之后就用z去计算出在当前z的情况下的PA,PB是多少,然后不断地重复这两个步骤直到收敛。
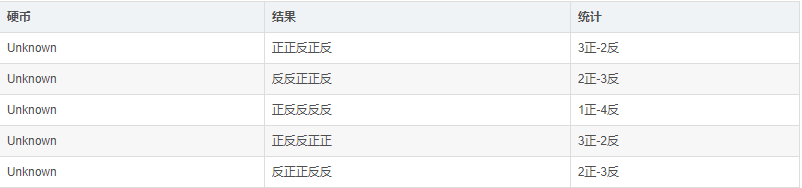
有了这个思想之后现在用这个思想来做一下这个例子,假设初始状态下PA=0.2, PB=0.7,然后我们根据这个概率去估计出z:
![]()
按照最大似然估计,z=(B,A,A,B,A),有了z之后我们反过来重新估计一下PA,PB:
PA = (2+1+2)/15 = 0.33
PB =(3+3)/10 = 0.6
可以看到PA,PB的值已经更新了,假设PA,PB的真实值0.4和0.5,那么你在不断地重复这两步你就会发现PA,PB在不断地靠近这两个真实值。
二 公式描述
假设目标函数表示为:
其中![]() 为概率分布的参数,在没有隐变量的情况下,我们求解L的最大值的套路是先对L取对数,将连乘的形式转换成累加的形式,然后就可以对未知数
为概率分布的参数,在没有隐变量的情况下,我们求解L的最大值的套路是先对L取对数,将连乘的形式转换成累加的形式,然后就可以对未知数![]() 进行求导,只需要求得导数为0的位置未知量的值即为目标函数的极大值。但是,如果概率分布中有隐变量存在时,我们用全概率公式把隐变量在上式中体现出来:
进行求导,只需要求得导数为0的位置未知量的值即为目标函数的极大值。但是,如果概率分布中有隐变量存在时,我们用全概率公式把隐变量在上式中体现出来:
全概率公式:
其中A需是一组完备事件组且都有正概率,则对任意B上式都成立。
![]()
两边同时取对数ln:
从上式中可以看出,如果要按照之前的套路,那就需要对上式进行求偏导,但是由于ln中还包含了求和项,在偏导数中的形式将会非常复杂,而且很难求得解析解。因此需要找到一种办法去求得解析解的近似解,这里就引入了EM算法。为了表述的方便性,在这里用![]() 代表,则:
代表,则:
对于求解近似解,EM算法采用的是迭代的方式不断地逼近真实值,假设第n次迭代的参数值为![]() ,第n+1次迭代的参数值为
,第n+1次迭代的参数值为![]() ,那么其实只要满足
,那么其实只要满足![]() 就可以不断地进行迭代。现在假设我们已经进行到了第n次迭代,也就是说
就可以不断地进行迭代。现在假设我们已经进行到了第n次迭代,也就是说![]() 目前是作为已知的值,那么来看一看
目前是作为已知的值,那么来看一看![]()
由于这里![]() 是作为常数的,因此右式中的第二项可以不用将隐变量体现出,化简如下:
是作为常数的,因此右式中的第二项可以不用将隐变量体现出,化简如下:
![]()
上式中,其实只需要关注求和里面的项就好了,做一个标注,记![]() 为I项,记为
为I项,记为![]() II项,接下来分别对这两项进行化简:
II项,接下来分别对这两项进行化简:
I项:
上式中的变换是因为
接下来还会用到Jensen不等式,Jensen不等式是这么描述的:
假设f(x)为凸函数,X是随机变量,那么:E[f(X)]>=f(E[X]),通俗的说法是函数的期望大于等于期望的函数。
特别地,如果f是严格凸函数,当且仅当 ,即 是常量时,上式取等号,即,如下图所示:
再观察一下I项,感觉有一些像能够用Jensen不等式进行再一次的化简,下面写的直观一点:
把![]() 当成X,那么上式
当成X,那么上式![]() 就是EX,又因为ln函数是凹函数,所以根据Jensen不等式有f(E[X])>=E[f(X)],则
就是EX,又因为ln函数是凹函数,所以根据Jensen不等式有f(E[X])>=E[f(X)],则
II项:
![]()
然后再把I-II合并起来看一下:
![]()
将上式代回![]() ,
,
将右边的这一大串记为![]() ,称为下边界函数,EM算法的目的是要取得目标函数的极大值,那么可以通过不断地提升下边界函数值来不断地提升目标函数的值,接下来,再看一下
,称为下边界函数,EM算法的目的是要取得目标函数的极大值,那么可以通过不断地提升下边界函数值来不断地提升目标函数的值,接下来,再看一下![]() ,将其化简为便于优化迭代的形式:
,将其化简为便于优化迭代的形式:
![]()
可以看到在等式的右边,由于我们之前的假设是![]() 是已知的,那么把已知量和未知量分开:
是已知的,那么把已知量和未知量分开:
上式中,等号右边的第一项中带未知项,第二项和第三项都是常数,所以接下来的过程就简单了,我们只要对这个式子求偏导![]() ,求得此时取极大值时
,求得此时取极大值时![]() 的取值,这个值就是进入到下一步迭代是的概率分布参数值
的取值,这个值就是进入到下一步迭代是的概率分布参数值![]() ,有了
,有了![]() 之后就可以获得,然后不断地迭代直到收敛。图示的话如下:
之后就可以获得,然后不断地迭代直到收敛。图示的话如下:
![]()
三 参考文献
1. 如何通俗理解EM算法
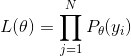


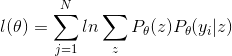

![=\sum_{j=1}^{N}\left [ ln\sum_{Z}P_\theta(y_j|z)P_\theta(z)-lnP_{\theta_n}(y_j)\right ]](http://img.e-com-net.com/image/info8/dcdff23c8d9a495896dc7fe6610c79db.gif)
![I-II\geqslant \sum_{j=1}^{N}\left [ \sum_{Z}P_{\theta_n}(z|y_j)ln\frac{P_{\theta}(y_j|z)P_\theta(z)}{P_{\theta_n}(z|y_j)}-\sum_{Z}P_{\theta_n}(z|y_j) lnP_{\theta_n}(y_j) \right]](http://img.e-com-net.com/image/info8/7f8d96d095854cfa8c3f146b24dbb406.gif)
![=\sum_{j=1}^{N} \sum_{Z}P_{\theta_n}(z|y_j) \left[ ln\frac{P_{\theta}(y_j|z)P_\theta(z)}{P_{\theta_n}(z|y_j)}-lnP_{\theta_n}(y_j) \right ]](http://img.e-com-net.com/image/info8/e1fdb3cd8fde4d75a4b6cc7f65566e4b.gif)
![=\sum_{j=1}^{N} \sum_{Z}P_{\theta_n}(z|y_j) \left[ ln\frac{P_{\theta}(y_j,z)}{P_{\theta_n}(z,y_j)} \right ]](http://img.e-com-net.com/image/info8/1d0079f9296d4cc3858f6bfaea98b6f1.gif)
![l(\theta)-l(\theta_n)\geqslant \sum_{j=1}^{N} \sum_{Z}P_{\theta_n}(z|y_j) \left[ ln\frac{P_{\theta}(y_j,z)}{P_{\theta_n}(z,y_j)} \right ]](http://img.e-com-net.com/image/info8/a2aed7ecae2242de8210df09740a1752.gif)