模型评价ROC\AUC\查准率\查全率\F-score\混淆矩阵\KS曲线\PR曲线等

一、ROC_AUC

1.1 ROC_AUC 概念

  AUC（Area Under Curve）是一个对二分类模型进行评价的指标，而这一指标是由ROC（Receiver Operating Characteristic Curve，受试者工作特征曲线）及其曲线下的面积组成，而ROC是由真阳性率（即tpr，表示正真正例的正确率）和假阳性率（即fpr，表示正真负例的正确率）绘制而成的曲线，是反映敏感性和特异性连续变量的综合指标，ROC曲线上每个点反映着对同一信号刺激的感受性。

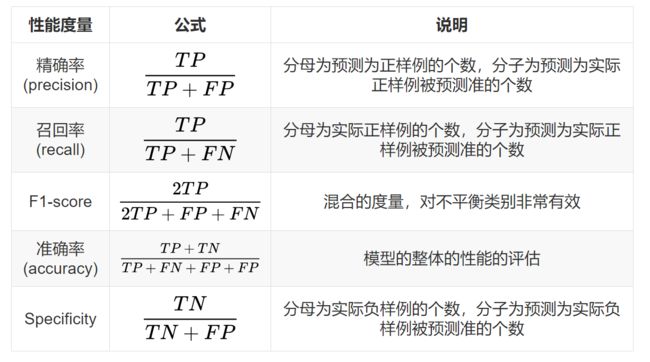
1.2 常见评价指标

  查准率、查全率和F-score是最为常用的二元分类结果评估指标。其中查准率和查全率这两个指标都只侧重于预测结果的某一个方面，并不能较全面地评价分类结果。而F-score则是更加“上层”的评估指标，它建立在前面两个指标的基础上，综合地考虑了分类结果的精确性和全面性。

• 查全率(Recall)，又叫召回率，查全率（Recall）就是所有对的样例，你找出了多少，或者说你判断对了多少。
• 查准率(Precision)，又叫精确率，缩写表示用P，查准率（Precision）就是你认为是对的样例中，到底有多少真是对的。
• Accuracy反应了分类器对整个样本的判定能力(即能将正的判定为正的，负的判定为负的)
  性能度量 公式 说明

1.3 sklearn.metrics.roc_curve()参数解释

sklearn.metrics.roc_curve(
    	    y_true,
    	    y_score,
    	    pos_label=None,
    	    sample_weight=None,
    	    drop_intermediate=True)

roc_curve()函数参数介绍：

• y_true：实际的样本标签值（这里只能用来处理二分类问题，即为{0，1}或者{true，false}，如果有多个标签，那么应该显式地给出pos_label。
• y_score：目标分数，被分类器识别成正例的分数（常用在method=“decision_function”、method=“proba_predict”）。
• pos_label：类型是int或str，作用是指定某个标签为正例。
• sample_weight：顾名思义，样本的权重，可选。
• drop_intermediate：布尔值，默认为True。

roc_curve()函数返回值介绍：

• fpr（False positive rate）：判断为正真负例的正确率。
• tpr（True positive rate）：判断为正真正例的正确率，即灵敏度，也就是召回率（Recall）。
• Thresholds：阙值。

TPR = TP / (TP+FN); 表示当前分到正样本中真实的正样本所占所有正样本的比例；

FPR = FP / (FP + TN); 表示当前被错误分到正样本类别中真实的负样本所占所有负样本总数的比例；

1.4 ROC_AUC 曲线

  ROC曲线是以FPR为横坐标，以TPR为纵坐标，以概率为阈值来度量模型正确识别正实例的比例与模型错误的把负实例识别成正实例的比例之间的权衡，TPR的增加必定以FPR的增加为代价，ROC曲线下方的面积是模型准确率的度量。
  为什么要用AUC作为二分类模型的评价指标呢？为什么不直接通过计算准确率来对模型进行评价呢？答案是这样的：机器学习中的很多模型对于分类问题的预测结果大多是概率，即属于某个类别的概率，如果计算准确率的话，那么就要把概率转化为类别，这就需要设定一个阈值，概率大于某个阈值的属于一类，概率小于某个阈值的属于另一类，而阈值的设定直接影响了准确率的计算。使用AUC可以解决这个问题，接下来详细介绍AUC的计算。
  例如，数据集一共有5个样本，真实类别为（1，0，0，1，0）；二分类机器学习模型，得到的预测结果为（0.5，0.6，0.4，0.7，0.3）。将预测结果转化为类别——预测结果降序排列，以每个预测值（概率值）作为阈值，即可得到类别。
  计算每个阈值下的“True Positive Rate”、“False Positive Rate”。以“True Positive Rate”作为纵轴，以“False Positive Rate”作为横轴，画出ROC曲线，ROC曲线下的面积，即为AUC的值。

# 导包
from sklearn.svm import SVC
from sklearn.datasets import load_iris
import numpy as np
from sklearn.metrics import auc, roc_curve  # 导入评价指标的计算公式
from scipy import interp  # 线性插值
from sklearn.model_selection import StratifiedKFold  # 将数据进行划分
import matplotlib.pyplot as plt

# 导入自带数据集，获取样本
from sklearn.datasets import make_blobs

二、混淆矩阵

2.1 混淆矩阵概念

  混淆矩阵是ROC曲线绘制的基础，返回值是一个误差矩阵，常用来可视化地评估监督学习算法的性能，同时它还是衡量分类型模型准确度中最基本、最直观、计算最简单的方法。此矩阵多用于判断分类器（Classifier）的优劣，适用于分类型的数据模型。在Sklearn中调用混淆矩阵的接口是函数sklearn.metrics.confusion_matrix，在Tensorflow中调用混淆矩阵的接口是函数tf.confusion_matrix。简单来说，混淆矩阵统计的是分类模型分对类、分错类的个数，然后把结果存储到一张表里，以更直观的类似DataFrame的格式展示出来。下表就是混淆矩阵的一个示例：

    在上表中，FN、FP、TN和TP的含义分别为：

• FN（False Negative）：代表将真实负将本划分为正样本的量，通俗的讲，假的被识别为了真的。
• FP（False Positive）：代表将真实负将本划分为负样本的量，通俗的讲，假的被识别为了假的。
• TN（True Negative）：代表将真实正将本划分为负样本的量，通俗的讲，真的被识别为了假的。
• TP（True Positive）：代表将真实正将本划分为正样本的量，通俗的讲，真的被识别为了真的。

2.2 代码

在这里插入代码片

  

三、KS 曲线

3.1 KS 曲线简介

  K-S曲线其实数据来源和本质和ROC曲线是一致的，只是ROC曲线是把真正率和假正率当作横纵轴，而K-S曲线是把真正率和假正率都当作是纵轴，横轴则由选定的阈值来充当。

  KS曲线又叫洛伦兹曲线。以TPR和FPR分别作为纵轴，以阈值作为横轴，画出两条曲线。KS曲线则是两条曲线的在每一个阈值下的差值。

  KS（Kolmogorov-Smirnov）值，KS=max(TPR-FPR)，即为TPR与FPR的差的最大值；

  KS值可以反映模型的最优区分效果，此时所取的阈值一般作为定义好坏用户的最优阈值。KS值越大，模型的预测准确性越好。KS值的取值范围是[0，1] ，一般，KS>0.2即可认为模型有比较好的预测准确性。

• KS<0.2：模型无鉴别能力；

• 0.2-0.4之间，模型勉强接受；

• 0.41-0.5之间，模型具有区别能力；

• 0.51-0.6之间，模型有很好的区别能力；

• 0.61-0.75之间，模型有非常好的区别能力；

• KS>0.75，模型异常，很有可能有问题。

3.2 总结

  由于KS值能找出模型中差异最大的一个分段，因此适合用于找阈值（cut_off），像评分卡这种就很适合用KS值来评估。但是KS值只能反映出哪个分段是区分最大的，而不能总体反映出所有分段的效果，因果AUC值更能胜任。 一般如果是如果任务更关注负样本，那么区分度肯定就很重要，此时K-S比AUC更合适用作模型评估，如果没什么特别的影响，那么就用AUC。

四、PR曲线

4.1 PR曲线简介

  P-R曲线的P就是查准率（Precision），R就是查全率（Recall）。以P作为横坐标，R作为纵坐标，就可以画出P-R曲线。

  对于同一个模型，通过调整分类阈值，可以得到不同的P-R值，从而可以得到一条曲线（纵坐标为P，横坐标为R）。通常随着分类阈值从大到小变化（大于阈值认为P），Precision减小，Recall增加。比较两个分类器好坏时，显然是查得又准又全的比较好，也就是的PR曲线越往坐标（1，1）的位置靠近越好。若一个学习器的P-R曲线被另一个学习器完全”包住”，则后者的性能优于前者。当存在交叉时，可以计算曲线围住面积，不太容易判断，但是可以通过平衡点（查准率=查全率，Break-Even Point，BEP）来判断。

4.2 PR曲线与ROC曲线对比

  与PR曲线相比，相对来讲ROC曲线会更稳定，在正负样本量都足够的情况下，ROC曲线足够反映模型的判断能力。而在正负样本分布得极不均匀(highly skewed datasets)的情况下（正样本极少），PRC比ROC能更有效地反映分类器对于整体分类情况的好坏。

  总之，只画一个曲线时，如果没有data imbalance,倾向于用ROC（更简洁，更好理解）。如果数据样本不均衡,分两种情况：

• 情况1：如正样本远小于负样本，PRC更敏感，因为用到了precision=(TP/(TP+FP))。

• 情况2：正样本远大于负样本，PRC和ROC差别不大，都不敏感。

  对于同一模型，PRC和ROC曲线都可以说明一定的问题，而且二者有一定的相关性，如果想评测模型效果，也可以把两条曲线都画出来综合评价。

4.3 总结

银行卡欺诈分类项目数据来源 https://blog.csdn.net/u010986753/article/details/98526886

import pandas as pd
data = pd.read_csv('.ipynb_checkpoints/py-data/creditcardfraud.csv')
#银行卡欺诈分类项目
data.shape#(284807, 31)

cls = data['Class'].value_counts()
cls


num = len(data)
num_fraud = len(data[data['Class']==1]) # 创建一个诈骗的dataframe
print('总交易笔数: ', num)
print('诈骗交易笔数：', num_fraud)
print('诈骗交易比例：{:.6f}'.format(num_fraud/num))
# 欺诈和正常交易可视化
import matplotlib.pyplot as plt
# 设置 plt 正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']

f, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(15,8))
bins = 50
ax1.hist(data.Time[data.Class == 1], bins = bins, color = 'deeppink')
ax1.set_title('诈骗交易')
ax2.hist(data.Time[data.Class == 0], bins = bins, color = 'deepskyblue')
ax2.set_title('正常交易')
plt.xlabel('时间')
plt.ylabel('交易次数')
plt.show()


# 混淆矩阵可视化
import numpy as np
import itertools
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix"', cmap=plt.cm.Blues):
    plt.figure()
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment='center',
                 color='white' if cm[i, j] > thresh else 'black')

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
    plt.show()


# 显示模型评估结果
def show_metrics():
    tp = cm[1, 1]
    fn = cm[1, 0]
    fp = cm[0, 1]
    tn = cm[0, 0]
    print('精确率: {:.3f}'.format(tp / (tp + fp)))
    print('召回率: {:.3f}'.format(tp / (tp + fn)))
    print('F1值: {:.3f}'.format(2 * (((tp / (tp + fp)) * (tp / (tp + fn))) / ((tp / (tp + fp)) + (tp / (tp + fn))))))


# 绘制精确率-召回率曲线
def plot_precision_recall():
    plt.step(recall, precision, color='b', alpha=0.2, where='post')
    plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
    plt.plot(recall, precision, linewidth=2)
    plt.xlim([0.0, 1])
    plt.ylim([0.0, 1.05])
    plt.xlabel('召回率')
    plt.ylabel('精确率')
    plt.title('精确率-召回率 曲线')
    plt.show();


# 对 Amount 进行数据规范化
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,precision_recall_curve
data.keys()
data['Amount_Norm'] = StandardScaler().fit_transform(data['Amount_Norm'].values.reshape(-1, 1))
# 特征选择

data['Amount_Norm'].shape#(284807,)
type(data['Amount_Norm'])#pandas.core.series.Series
data['Amount_Norm'].values.reshape(-1, 1).shape#(284807, 1)
type(data['Amount_Norm'].values.reshape(-1, 1))#numpy.ndarray

y = np.array(data.Class.tolist())
data.keys()
data = data.drop(['Time', 'Amount_Norm', 'Class'], axis=1)
X = np.array(data.as_matrix())
# 准备训练集和测试集
train_x, test_x, train_y, test_y = train_test_split(X, y, test_size=0.1, random_state=33)
train_x.shape, test_x.shape#((256326, 29), (28481, 29))
# 逻辑回归分类
clf = LogisticRegression()
clf.fit(train_x, train_y)
predict_y = clf.predict(test_x)
# 预测样本的置信分数
score_y = clf.decision_function(test_x)
# 计算混淆矩阵，并显示
cm = confusion_matrix(test_y, predict_y)
class_names = [0, 1]
# 显示混淆矩阵
plot_confusion_matrix(cm, classes=class_names, title='逻辑回归 混淆矩阵')
# 显示模型评估分数
show_metrics()
# 计算精确率，召回率，阈值用于可视化
precision, recall, thresholds = precision_recall_curve(test_y, score_y)
plot_precision_recall()

有趣的事，Python永远不会缺席

欢迎关注小婷儿的博客

    文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解

    如需转发，请注明出处：小婷儿的博客python    https://www.cnblogs.com/xxtalhr/

博客园 https://www.cnblogs.com/xxtalhr/

CSDN https://blog.csdn.net/u010986753

有问题请在博客下留言或加作者：
     微信：tinghai87605025 联系我加微信群
     QQ ：87605025
     python QQ交流群：py_data 483766429

培训说明

OCP培训说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

OCM培训说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA

     小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。