分形图总结

 分形总结

       前一段时间一直在画分形，今天终于坐下来把我画的和大家分享一下。

       先来名词解释吧。1975年，数学家曼德布罗特(B. B. Mandelbrot)出版了著作《分形、机遇和维数》，标志着分形理论的诞生，这是一门力图以数学方法，模拟自然界存在的、及科学研究中出现的那些看似无规律的各种现象的学科。在过去的几十年里，分形在物理学、材料科学、地质勘探、乃至股价的预测等方面都得到了广泛的应用或密切的注意，并且由于分形的引入，使得一些学科焕发了新的活力。

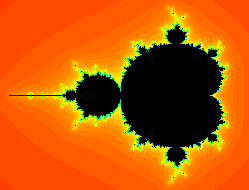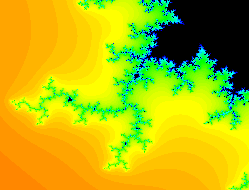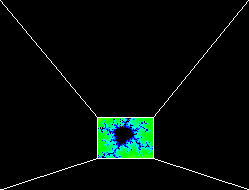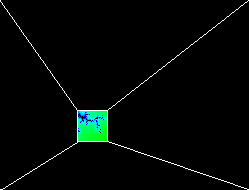
       而分型图则无疑是这个学科中格外引人关注的一部分，分形图主要表现为部分的自相似性，充分表现了数学的简单、和谐、统一的内涵。借助计算机，数学家们创造出了无比神奇的作品。由这一点出发，可以说，艺术家已经开始漫步于科学领地，而科学家也从此跨入了神圣的艺术殿堂。其中比较为人熟知的图形有三分康托集、谢宾斯基地毯、谢宾斯基三角形、科赫曲线等，而最让人惊叹的还数神奇的曼德勃罗集——无限放大的过程中呈现出无穷的变化。

曼德勃罗集

 

分型图的神奇来源于他的自相似性，而这通过计算机程序的递归迭代算法得以轻松实现，以下分享一下我画的几个作品。

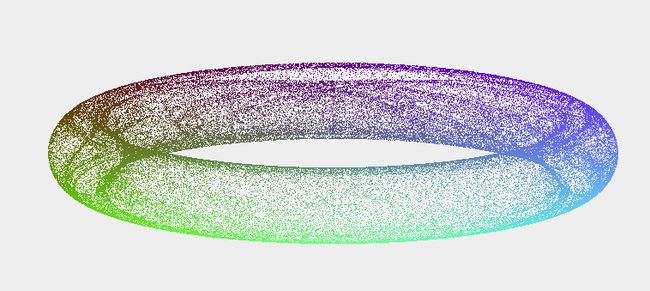
       前两个是根据胡哥给的公式画的，通过简单的递归迭代就能实现，难点在于颜色的设置。一开始我也没有头绪，后来我慢慢摸索，先算出图像的宽度长度，然后以此为基准，用系数把图形的位置转化成0-255的值，以此来设置颜色的三个参数，使图形总体呈现渐变的效果，只是好像不是很好看。。。。

       谢宾斯基垫片和三角形，通过分析最简单的部分图形，不难通过递归实现。困难的在科赫曲线，一开始搞了好久我都没弄明白，因为不知如何找到不同位置直线的“凸起点”，因为直线倾斜时好难找，通过方程计算坐标又好麻烦。。。。

       后来，我偷了个懒，换了种方法，找到两个顶点之间连线的三等分点，一次得到两个“凸起点”，于是，科赫曲线中所有的点都成为了“三等分点”，最后好歹实现了。。。当然，过程中还出现了另一个问题，那就是在前一层中画过的线在后面均产生了“多余”，很不好看。为了改进这点，我一开始也没有思路，想到用再画一条白线盖住原来的黑线的方法。。。。当然，没有成功，因为后面产生了误差，很多线都没能盖住。后来，我看到了另一位学长写的日志，才豁然开朗——原来只要简单加一个判断语句，让函数递归到最后一层时才画线，这样有没有了之前多余线的烦恼。

以下是截图与代码：

1、

 

g.clearRect(0, 150, 1500, 1000);
   double xt = 1;
      double yt = 1;
      for(int  i=0;i<100000;i++){
       double tx = xt;
       double ty = yt;

       //核心公式
       xt = Math.sin(-2*ty)-Math.cos(-2*tx);
       yt = Math.sin(-1.2*tx)-Math.cos(2*ty);

       int xn = (int)(xt*fd*100)+600;
       int yn = (int)(yt*fd*100)+400;
       if (xn>maxX)maxX = xn;
       if(yn>maxY)maxY = yn;
       if(xn       if(yn       int x = (int)(xt*100)+300;
       int y = (int)(yt*100)+300;

       //设置颜色
       double p1 = 255.0/398,p2 = 255.0/389;
       int t1 = (int)(p1*(x-101)),t2 = (int)(p2*(y-101));
       int r2 = 255-t2 ,g2 = t1,b2 = t2;
       g.setColor(new Color(r2,g2,b2));
       if(yn>80)g.drawLine(xn, yn, xn, yn);
      } 

2、

 

 

g.clearRect(0, 150, 1500, 1000);
   double xt = 1;
      double yt = 1;
      for(int  i=0;i<100000;i++){
       double tx = xt;
       double ty = yt;
       xt = -6.56*Math.sin(1.4*tx)-Math.sin(1.56*ty);
       yt = 1.4*Math.cos(1.4*tx)+Math.cos(1.56*ty);
       int xn = (int)(xt*fd*40)+600;
       int yn = (int)(yt*fd*40)+395;
       if(xn>maxX) maxX = xn;
       if(yn>maxY) maxY = yn;
       if(xn       if(yn       //设置颜色
       int x = (int)(xt*40)+398;
       int y = (int)(yt*40)+395;
       double p1 = 255.0/604,p2 = 255.0/190;
       int t1 = (int)(p1*(x-96)),t2 = (int)(p2*(y-300));
       int r1 = 100 ,g1 = t2,b1 = (t1+t1)/2;
       g.setColor(new Color(r1,g1,b1));
       if(yn>80)g.drawLine(xn, yn, xn, yn); 
      }

 3、谢宾斯基三角形

 

//画谢宾斯基三角形的方法
 public void drawMTir(int x1,int y1,int x2,int y2,int x3,int y3){
  if(ceng == 0){
   drawTri(x1,y1,x2,y2,x3,y3);
  }
  else{
   drawNext1(x1,y1,x2,y2,x3,y3,ceng);
  }
 }
 //画三角形的递归方法
 private void drawNext1(int x1,int y1,int x2,int y2,int x3,int y3,int count) {
  count--;
  if(count<0)return;
  drawTri(x1,y1,x2,y2,x3,y3);
  drawTri((x1+x2)/2,(y1+y2)/2,(x2+x3)/2,(y2+y3)/2,(x3+x1)/2,(y3+y1)/2);
  
  drawNext1(x1,y1,(x1+x2)/2,(y1+y2)/2,(x3+x1)/2,(y3+y1)/2,count);
  drawNext1((x1+x2)/2,(y1+y2)/2,x2,y2,(x3+x2)/2,(y3+y2)/2,count);
  drawNext1((x1+x3)/2,(y1+y3)/2,(x2+x3)/2,(y2+y3)/2,x3,y3,count);
  
 }

 

 4、谢宾斯基垫片

 

//画谢宾斯基垫片的方法
 private void drawXie(int x, int y, int width) {
  x += 100;
  y += 100;
  g.drawRect(x,y,width,width);
  g.fillRect(x+width/3, y+width/3, width/3,  width/3);
  drawNextXie(x+width/3, y+width/3, width/3,ceng);
 }
 //画谢宾斯基的递归方法
 private void drawNextXie(int x, int y, int w,int count) {
  if(count-- < 0){
   return;
  }
  w/=3;
  g.fillRect(x-2*w, y-2*w, w, w);
  g.fillRect(x+w, y-2*w, w, w);
  g.fillRect(x+4*w, y-2*w, w, w);
  g.fillRect(x-2*w, y+w, w, w);
  g.fillRect(x+4*w, y+w, w, w);
  g.fillRect(x-2*w, y+4*w, w, w);
  g.fillRect(x+w, y+4*w, w, w);
  g.fillRect(x+4*w, y+4*w, w, w);
  drawNextXie(x-2*w , y-2*w, w, count);
  drawNextXie(x+w , y-2*w, w,count);
  drawNextXie(x+4*w , y-2*w, w,count);
  drawNextXie(x-2*w , y+w, w,count);
  drawNextXie(x+4*w , y+w, w,count);
  drawNextXie(x-2*w , y+4*w, w,count);
  drawNextXie(x+w , y+4*w, w,count);
  drawNextXie(x+4*w , y+4*w, w,count);
 }

5、科赫曲线

 

  //画科赫曲线的方法
 public void drawKehe(int x1,int y1,int x5,int y5){
  if(ceng == 0){
   g.drawLine(x1, y1, x5, y5);
  }else if(ceng == 1){
   int x2 = (2*x1+x5)/3,y2 = (2*y1+y5)/3,
     x3 = (x1+x5)/2,y3 = (int)((y1+y2)/2-Math.sqrt(3)*(x5-x1)/6),
     x4 = (x1+2*x5)/3,y4 = (y1+2*y5)/3;
   drawFour(x1,y1,x2,(2*y1+y2)/3,x3,y3,x4,y4,x5,y5);
  }else {
   int x2 = (2*x1+x5)/3,y2 = (2*y1+y5)/3,
     x3 = (x1+x5)/2,y3 = (int)((y1+y2)/2-Math.sqrt(3)*(x5-x1)/6),
     x4 = (x1+2*x5)/3,y4 = (y1+2*y5)/3;
  drawNextKehe(x1,y1,x2,y2,x3,y3,ceng-1);
  drawNextKehe(x3,y3,x4,y4,x5,y5,ceng-1);
  }
 }
 //画科赫曲线的递归方法
 private void drawNextKehe(int x1, int y1, int x5, int y5,int x9,int y9,int count) {
  count--;
  if(count<0)return; 
  int x2 = (2*x1+x5)/3,y2 = (2*y1+y5)/3;
  int x3 = (2*x1+x9)/3,y3 = (2*y1+y9)/3;
  int x4 = (x1+2*x5)/3,y4 = (y1+2*y5)/3;
  int x6 = (2*x5+x9)/3,y6 = (2*y5+y9)/3;
  int x7 = (x1+2*x9)/3,y7 = (y1+2*y9)/3;
  int x8 = (x5+2*x9)/3,y8 = (y5+2*y9)/3;
   
  if(count == 0)drawEight(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7,x8,y8,x9,y9); 
   
  drawNextKehe(x1,y1,x2,y2,x3,y3,count);
  drawNextKehe(x3,y3,x4,y4,x5,y5,count);
  drawNextKehe(x5,y5,x6,y6,x7,y7,count);
  drawNextKehe(x7,y7,x8,y8,x9,y9,count);
 }
   //画8条线的方法
 private void drawEight(int x1,int y1,int x2,int y2,int x3,int y3,int x4,int y4,int x5,int y5,int x6,int y6,int x7,int y7,int x8,int y8,int x9,int y9){
  g.drawLine(x1, y1, x2, y2);
  g.drawLine(x2, y2, x3, y3);
  g.drawLine(x3, y3, x4, y4);
  g.drawLine(x4, y4, x5, y5);
  g.drawLine(x5, y5, x6, y6);
  g.drawLine(x6, y6, x7, y7);
  g.drawLine(x7, y7, x8, y8);
  g.drawLine(x8, y8, x9, y9); 
 }
 //画4条线的方法
 private void drawFour(int x1,int y1,int x2,int y2,int x3,int y3,int x4,int y4,int x5,int y5){
  g.drawLine(x1, y1, x2, y2);
  g.drawLine(x2, y2, x3, y3);
  g.drawLine(x3, y3, x4, y4);
  g.drawLine(x4, y4, x5, y5);
 }