数据结构-动态查找树表与平衡二叉树 红黑树简单介绍
参考资料
数据结构(严蔚敏)
大话数据结构
百度百科
https://blog.csdn.net/lpp0900320123/article/details/39524947
https://mp.weixin.qq.com/s/jz1ajDUygZ7sXLQFHyfjWA(红黑树的简单介绍)
https://blog.csdn.net/vesper305/article/details/13614403(平衡二叉树的旋转讲的非常透彻,比某些书好懂多了)
二叉排序树(二叉查找树 BST 动态查找树表)
定义
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
第一条和第二条规定了根节点和左右子树的关系,而点三条则是一种递归的定义。
构建举例
比如给了一组数据 20,46,55,57,16,78,45,12,43,32.我们可以构建如下的二叉排序树
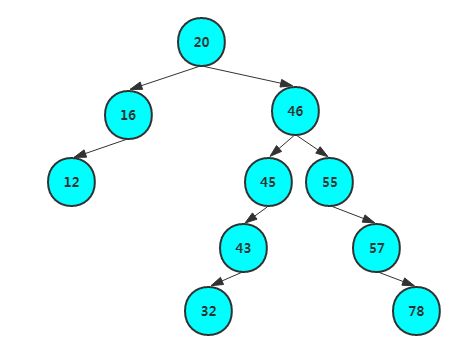
思路就是以第一个数字为根节点,下面的数字与根节点比较,大则查找右子树,小查找左子树。如果查找的子树为空,则插入到该位置
注意:构建完成的二叉排序树其实已经是个有序树了。进行二叉树的中跟遍历能得到有序的数组
查找算法思路
1.若根结点的关键字值等于查找的关键字,成功。
2.否则,若小于根结点的关键字值,递归查左子树。
3.若大于根结点的关键字值,递归查右子树。
4.若子树为空,查找不成功。
查找性能O(logn)
插入算法思路
这个和构建有点重复了,在查找过程中,当树中不存在关键字等于给定值的结点时再进行插入。更构建的思路一致。
删除算法思路
分三种情况讨论
1.删除的是叶子节点
此种情况最简单,直接删除节点即可
2.删除的节点只有左子树或只有右子树
此种情况也比较简单,删除节点后连接节点的单个子树和双亲节点即可。如图:

删除59节点
3.删除的节点同时有左子树和右子树
前面在二叉树的构建中,我们说到,二叉树建立的是一个有序树,那么便有了思路。可以找到有序序列中被删除节点的前驱或后继代替当前被删除的节点。
举例:
删除上图的46节点,那么46的中根遍历的前驱是哪个呢?很明显是45.那么删除节点后的树是这样的:

弊端
如果给出一个序列是这样的 1,2,3,4,5,66,77.那么它的二叉排序树是这样的:

这种二叉排序树明显查找明显是遍历的效果,因此在这种特殊情况下,它的查找效率为O(n),虽然这是特殊情况,但是在最坏的情况下确实会发生。为了避免这种情况,就引入了二叉平衡树。
二叉平衡树(AVL树 AVL来源于发明者首字母)
什么是二叉平衡树
定义什么的不知道,我们可以先不管定义,记住二叉平衡树首先得是个二叉排序树,在此前提下,所有节点的平衡因子的绝对值小于等于1
平衡因子
一个节点的平衡因子=该节点左子树的高度-该节点右子树的高度。当所有节点的平衡因子绝对值都<=1就是平衡二叉树
举几个例子
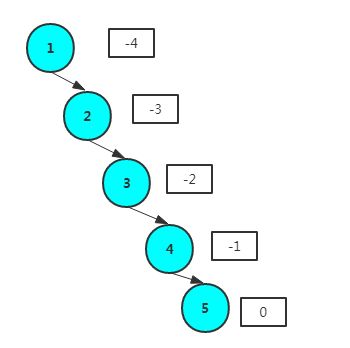

上面这棵便是平衡二叉树
构建思路
导致平衡二叉树不平衡的原因有以下几种情况
- 对 r 的左儿子的左子树进行一次插入(LL)
- 对 r 的左儿子的右子树进行一次插入(LR)
- 对 r 的右儿子的左子树进行一次插入(RL)
- 对 r 的右儿子的右子树进行一次插入(RR)
1,2两种情况只要对最小不平衡子树进行右旋转和左旋转即可
3,4两种情况稍显复杂,3需要先进行右旋转,再进行左旋转。而四需要先进行左旋转,再进行右旋转。
所以,平衡二叉树和二叉排序树的构建基本一致,但是构建过程中需要检查树是否平衡。比如上面的这棵树,如果我们要加上31节点,按照二叉排序树的构建结果是这样的

可以看到整棵树构建完了之后,不再平衡,而图中红框部分是导致不平衡的原因,需要使用二叉树的旋转来确保红框中的树保持平衡。我们看到平衡因子都大于等于0,那么进行树的右(顺时针)旋转 最终得到:
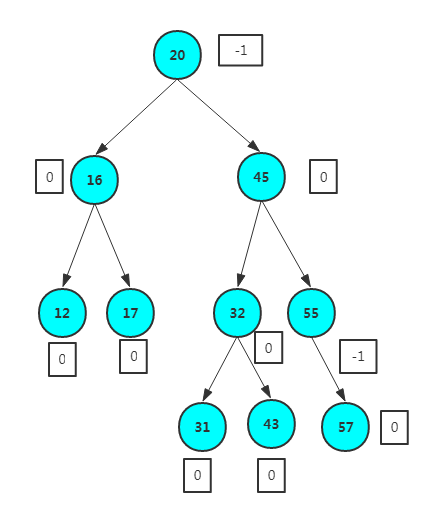
同样,如果平衡因子都小于等于0,那么进行树的左(逆时针)旋转
具体的过程和算法可以参照
https://blog.csdn.net/vesper305/article/details/13614403
(强推,非常好懂)
盗几张图-。-


注意C的高度比AB都大一
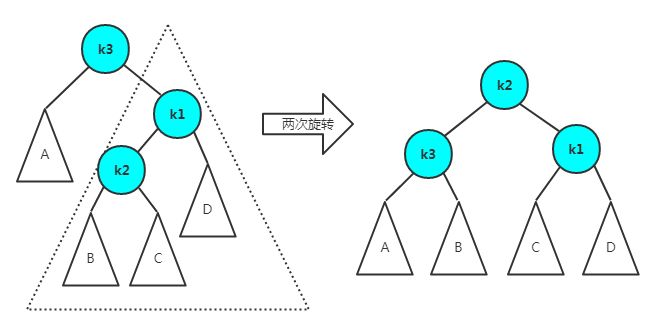

注意:ABCD等高
需要先对虚三角中的子树进行一次旋转
实际情况下,B和C一般有一个为空树
所以我们可以得出,平衡二叉树是由二叉排序树构建过程中,进行平衡算法过后形成的树。
查找效率
在平衡二叉树进行查找的过程和二叉排序树一样,只不过二叉排序树不稳定,会出现斜向一边的情况降低效率。
假设平衡二叉树一共有N个节点那么不难推测
h约等于 log2N l o g 2 N
平衡二叉树查找时间复杂度O(logn)
2018 5月15日更新
红黑树 (BRT)
除了平衡二叉树,红黑树是另一种自平衡的二叉树
红黑树的定义
- 1.节点是红色或黑色。
- 2.根节点是黑色。
- 3.每个叶子节点都是黑色的空节点(NIL节点)。
- 4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
注:程序员小灰: 标颜色是为了更好地通过颜色相关的规则来检验树的平衡性,打一个比方,就像是咱们中学解几何问题需要作辅助线一样。
红黑树的插入
为了保持红黑树的平衡,在插入节点时需要查看是否插入后影响红黑树的平衡(即定义中的五项是否仍然遵守)。如果影响了平衡性,需要对红黑树作变色和旋转来维持红黑树的平衡。
插入的节点固定初始颜色为红色,如果破坏了第四条或者第五条,需要进行变色(红变黑),且变色会引起连锁反应。同时还要进行旋转(就是在平衡二叉树中讲到的左右旋转)来保持平衡性。最复杂时需要进行 变色 -> 左(右)旋转 -> 变色 -> 右(左)旋转 -> 变色
红黑树的插入可以参照https://mp.weixin.qq.com/s/jz1ajDUygZ7sXLQFHyfjWA
红黑树的应用
在Java中TreeSet和TreeMap都用到了红黑树,而JDK 8以后,HashMap的设计也加入了红黑树
BST AVL BRT对比:
相比于AVL BRT,BST有明显的劣势即容易偏向一边,变成“瘸子树”,导致树的高度过高,查找变成线性查找,降低性能。而AVL和BRT通过自平衡,有效降低高度,提高查找性能。
AVL BRT查找对比:
AVL查找最好最坏都是O(lgn); RBT查找基本维持在O(lgn),最坏比AVL略差(2lg(n+1)),但远好于BST。
AVL BRT插入删除比较:
1.插入时,AVL和RBT都最多需要2次旋转;删除时,AVL最多需要lgN次旋转,而RBT最多需要3次旋转;
2.RBT旋转平衡时,需要变色操作,在O(lgN)数量级上,但操作简单、速度快;
3.二者插入删除的代价主要消耗在查找操作上,都与O(lgN)成正比;
AVL BRT插入删除比较复杂,有兴趣的同学去维基百科和参考链接看看。
