Logistic回归及梯度上升算法

开始学习机器学习算法的时候就接触了Logistic回归及梯度下降法，但是当时并没有深入去自己推导一下公式，写一写代码，现在学习xgboost的时候又碰到Logistic回归相关的知识，干脆自己推一遍，写一下代码吧。。

逻辑回归

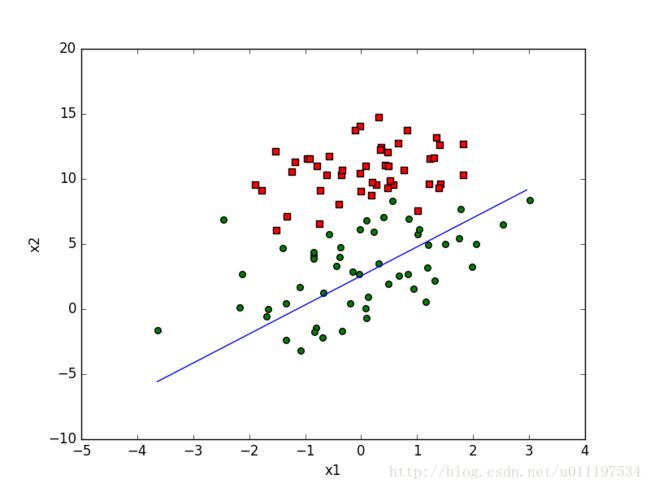
逻辑回归可以用来进行回归与分类，两者仅有略微不同，主体算法是一样的，本文以分类进行讲解。如下图二分类问题，我们希望找到一个直线（高维空间为超平面）来将数据划分开。

这样的线性边界可以表示为： θ0x1+θ1x2+...+θmxm=θTx θ 0 x 1 + θ 1 x 2 + . . . + θ m x m = θ T x
上式右边x为向量。
我们取预测函数为Sigmoid函数，Sigmoid函数有一个很棒的特点是它的导数 f′(x)=f(x)(1−f(x)) f ′ ( x ) = f ( x ) ( 1 − f ( x ) )
则预测函数可表示为：

P(y=1|x;θ)=hθ(x) P ( y = 1 | x ; θ ) = h θ ( x )

P(y=0|x;θ)=1−hθ(x) P ( y = 0 | x ; θ ) = 1 − h θ ( x )

将这两个式子合并一下：

P(y|x;θ)=(hθ(x))y(1−hθ(x))1−y P ( y | x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y

显然：
当y=0的时候上式等价于 P(y=0|x;θ)=1−hθ(x) P ( y = 0 | x ; θ ) = 1 − h θ ( x )
当y=1的时候上式等价于 P(y=1|x;θ)=hθ(x) P ( y = 1 | x ; θ ) = h θ ( x )

取似然函数 L(θ)=∏mi=1(hθ(x(i)))yi(1−hθ(x(i)))1−yi L ( θ ) = ∏ i = 1 m ( h θ ( x ( i ) ) ) y i ( 1 − h θ ( x ( i ) ) ) 1 − y i
我们的目的就是求解似然函数的最大值，为了方便求解，我们取对数似然函数如下：

logL(θ)=∑i=1m(yiloghθ(x(i))+(1−yi)log(1−hθ(x(i)))) l o g L ( θ ) = ∑ i = 1 m ( y i l o g h θ ( x ( i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x ( i ) ) ) )

如此，我们就可以使用如下的式子进行梯度上升算法迭代更新 θ θ 的取值：

θj=θj+α∂logL(θ))∂θj θ j = θ j + α ∂ l o g L ( θ ) ) ∂ θ j

下面求解 ∂logL(θ))∂θ ∂ l o g L ( θ ) ) ∂ θ

∂logL(θ))∂θj=∑i=1m(yi1hθ(x(i))+(1−yi)11−hθ(x(i)))∂hθ(x(i))∂θj ∂ l o g L ( θ ) ) ∂ θ j = ∑ i = 1 m ( y i 1 h θ ( x ( i ) ) + ( 1 − y i ) 1 1 − h θ ( x ( i ) ) ) ∂ h θ ( x ( i ) ) ∂ θ j

=∑i=1m(yi1g(θTx(i))+(1−yi)11−g(θTx(i)))g(θTx(i))(1−g(θTx(i)))x(i) = ∑ i = 1 m ( y i 1 g ( θ T x ( i ) ) + ( 1 − y i ) 1 1 − g ( θ T x ( i ) ) ) g ( θ T x ( i ) ) ( 1 − g ( θ T x ( i ) ) ) x ( i )

=∑i=1m(yi(1−g(θTx(i)))−(1−yi)g(θTx(i)))x(i) = ∑ i = 1 m ( y i ( 1 − g ( θ T x ( i ) ) ) − ( 1 − y i ) g ( θ T x ( i ) ) ) x ( i )

=∑i=1m(yi−g(θTx(i)))x(i) = ∑ i = 1 m ( y i − g ( θ T x ( i ) ) ) x ( i )

=∑i=1m(yi−hθ(x(i)))x(i) = ∑ i = 1 m ( y i − h θ ( x ( i ) ) ) x ( i )

所以权重的迭代更新式为：

θj=θj+α∑i=1m(yi−hθ(x(i)))x(i) θ j = θ j + α ∑ i = 1 m ( y i − h θ ( x ( i ) ) ) x ( i )

其中 α α 为更新率

梯度上升

有了以上的逻辑回归的理论基础，下面我们编程实现这一步骤。就以第一张图的样本为例进行，样本维数为2维，采用梯度上升算法进行迭代。
迭代步数自己选择

批量梯度上升
批量梯度上升每进行一次迭代更新就会计算所有样本，因此得到的模型正确率比较高，但同时计算复杂度高，算法耗时。计算过程如下：
1.首先根据权重和训练样本计算估计值

h=⎛⎝⎜⎜⎜⎜⎜x(1)1x(2)1...x(m)1x(1)2x(2)2...x(m)2x(1)3x(2)3...x(m)3⎞⎠⎟⎟⎟⎟⎟⎛⎝⎜⎜θ1θ2θ3⎞⎠⎟⎟=⎛⎝⎜⎜⎜⎜y1^y2^...ym^⎞⎠⎟⎟⎟⎟ h = ( x 1 ( 1 ) x 2 ( 1 ) x 3 ( 1 ) x 1 ( 2 ) x 2 ( 2 ) x 3 ( 2 ) . . . . . . . . . x 1 ( m ) x 2 ( m ) x 3 ( m ) ) ( θ 1 θ 2 θ 3 ) = ( y 1 ^ y 2 ^ . . . y m ^ )

2.计算误差

error=y−ŷ =⎛⎝⎜⎜⎜⎜y1y2...ym⎞⎠⎟⎟⎟⎟−⎛⎝⎜⎜⎜⎜y1^y2^...ym^⎞⎠⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜e1e2...em⎞⎠⎟⎟⎟⎟ e r r o r = y − y ^ = ( y 1 y 2 . . . y m ) − ( y 1 ^ y 2 ^ . . . y m ^ ) = ( e 1 e 2 . . . e m )

3.迭代更新

w=w+⎛⎝⎜⎜⎜x(1)1x(1)2x(1)3x(2)1x(2)2x(2)3.........x(m)1x(m)2x(m)3⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜⎜e1e2...em⎞⎠⎟⎟⎟⎟→⎛⎝⎜⎜Δθ1Δθ2Δθ3⎞⎠⎟⎟ w = w + ( x 1 ( 1 ) x 1 ( 2 ) . . . x 1 ( m ) x 2 ( 1 ) x 2 ( 2 ) . . . x 2 ( m ) x 3 ( 1 ) x 3 ( 2 ) . . . x 3 ( m ) ) ( e 1 e 2 . . . e m ) → ( Δ θ 1 Δ θ 2 Δ θ 3 )

随机梯度上升
根据样本数量进行迭代，每计算一个样本就进行一次更新，过程如下：
1.计算 x(i) x ( i ) 样本对应的估计值

h=(x(i)1x(i)2x(i)3)⎛⎝⎜⎜θ1θ2θ3⎞⎠⎟⎟ h = ( x 1 ( i ) x 2 ( i ) x 3 ( i ) ) ( θ 1 θ 2 θ 3 )

2.计算误差

error=yi−h(number) e r r o r = y i − h ( n u m b e r )

注意，此处的误差是个数，不再是个向量
3.迭代更新

w=w+α⎛⎝⎜⎜⎜x(i)1x(i)2x(i)3⎞⎠⎟⎟⎟error w = w + α ( x 1 ( i ) x 2 ( i ) x 3 ( i ) ) e r r o r

以上步骤更新m次。

代码如下

import numpy as np
import re
from pandas import DataFrame
import time as time
import matplotlib.pyplot as plt
import math

def get_data(filename):                 #读取数据
    f = open(filename)
    data = DataFrame(columns=['x0','x1','x2','label']) #构造DataFrame存放数据，列名为x与y
    line = f.readline()
    line = line.strip()
    p = re.compile(r'\s+')              #由于数据由若干个空格分隔，构造正则表达式分隔
    while line:
        line = line.strip()
        linedata = p.split(line)
        data.set_value(len(data),['x0','x1','x2','label'],[1,float(linedata[0]),float(linedata[1]),int(linedata[2])]) #数据存入DataFrame
        line = f.readline()
    return np.array(data.loc[:,['x0','x1','x2']]),np.array(data['label'])
def sigmoid(x):
    return 1.0/(1+np.exp(-x))
def stocGradAscent(dataMat,labelMat,alpha = 0.01):   #随机梯度上升
    start_time = time.time()                         #记录程序开始时间
    m,n = dataMat.shape
    weights = np.ones((n,1))                         #分配权值为1
    for i in range(m):
        h = sigmoid(np.dot(dataMat[i],weights).astype('int64')) #注意：这里两个二维数组做内积后得到的dtype是object,需要转换成int64
        error = labelMat[i]-h                        #误差
        weights = weights + alpha*dataMat[i].reshape((3,1))*error #更新权重
    duration = time.time()-start_time
    print('time:',duration)
    return weights
def gradAscent(dataMat,labelMat,alpha = 0.01,maxstep = 1000): #批量梯度上升
    start_time = time.time()
    m,n = dataMat.shape
    weights = np.ones((n,1))
    for i in range(maxstep):
        h = sigmoid(np.dot(dataMat,weights).astype('int64'))  #这里直接进行矩阵运算
        labelMat = labelMat.reshape((100,1))                  #label本为一维,转成2维
        error = labelMat-h                                    #批量计算误差
        weights = weights + alpha*np.dot(dataMat.T,error)     #更新权重
    duration = time.time()-start_time
    print('time:',duration)
    return weights
def betterStoGradAscent(dataMat,labelMat,alpha = 0.01,maxstep = 150):
    start_time = time.time()
    m,n = dataMat.shape
    weights = np.ones((n,1))
    for j in range(maxstep):
        for i in range(m):
            alpha = 4/(1+i+j) + 0.01                         #设置更新率随迭代而减小
            h = sigmoid(np.dot(dataMat[i],weights).astype('int64'))
            error = labelMat[i]-h
            weights = weights + alpha*dataMat[i].reshape((3,1))*error
    duration = time.time()-start_time
    print('time:',duration)
    return weights
def show(dataMat, labelMat, weights):
    #dataMat = np.mat(dataMat)
    #labelMat = np.mat(labelMat)
    m,n = dataMat.shape
    min_x = min(dataMat[:, 1])
    max_x = max(dataMat[:, 1])
    xcoord1 = []; ycoord1 = []
    xcoord2 = []; ycoord2 = []
    for i in range(m):
        if int(labelMat[i]) == 0:
            xcoord1.append(dataMat[i, 1]); ycoord1.append(dataMat[i, 2])
        elif int(labelMat[i]) == 1:
            xcoord2.append(dataMat[i, 1]); ycoord2.append(dataMat[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcoord1, ycoord1, s=30, c="red", marker="s")
    ax.scatter(xcoord2, ycoord2, s=30, c="green")
    x = np.arange(min_x, max_x, 0.1)
    y = (-float(weights[0]) - float(weights[1])*x) / float(weights[2])
    ax.plot(x, y)
    plt.xlabel("x1"); plt.ylabel("x2")
    plt.show()

if __name__=='__main__':
    dataMat,labelMat = get_data('data1.txt')
    weights = gradAscent(dataMat,labelMat)
    show(dataMat,labelMat,weights)

效果
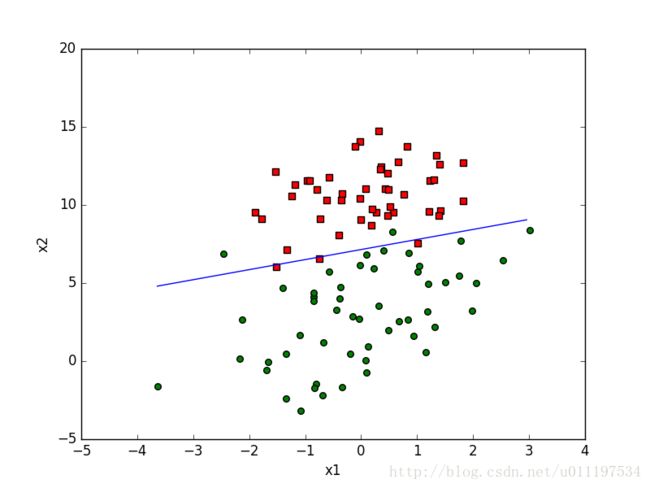
随机梯度：

批量梯度：

改进的随机梯度：
实际就是进行多次随机梯度，学习率随着迭代步数而减小。