数据分析系列：绩效（效率）评价与python实现（层析分析、topsis、DEA）

当分析一个项目是否可行，或多个决策中挑选出最优的一个进行执行，对以往的项目或人员进行绩效评价时，我们需要对一项业务或人员的绩效（效率）进行打分。这就是绩效（效率）评价的目标。

假设有下面一个案例，我们对一个进行产品进行用户增长的广告投放，假设我们有多个广告承接商可以选择。具体的我们应该选择哪一个广告承接商？这就可以用一些绩效评价的方法解决，可用户绩效（效率）评价的方法非常多，这里只介绍层析分析法，topsis，和数据包络分析（DEA），并利用python进行实现。

具体来说，当我们可以观测到每种决策的属性指标时（比如某一决策大拉新转化率、复购率、投入成本等），我们可以使用层析分析法和topsis方法。其中，层析分析法将目标拆解为若干因素，每个因素的权重主观定义，每个因素又由决策的指标特征决定，于是可以通过决策特征带入层析网络，对决策进行评价（层析结构有点类似于神经网络）。topsis通过计算每种决策指标特征与最佳/最差决策指标特征的距离来对决策的绩效进行打分。

当决策的产出可以观察时（比如决策带来的用户增长或带来的总价值），我们可以通过比较每种决策相同的投入时，产出的大小，产出越大越好。或每种决策产出向同时，投入的大小，投入越小越好。具体的我们可以建立数据包络分析模型（DEA），分析每个决策的效率。其中DEA还分为CRS（也称为CCR）和VRS（也称为BCC）等模型。CRS表示规模收益固定模型，VRS表示考虑规模收益可变模型。

下面对层析分析法、topsis和DEA的进行介绍。

一、层析分析法

层次分析法（analysis hierarchy process,简称AHP）是用系统分析的方法，对评价对象依评价目的所确定的总目标进行连续性分解，得到各级（各层）评价子目标，并以最下层作为衡量目标达到程度的评价指标，然后依据这些指标计算出一综合评分指数对评价对象的总目标进行评价，依其大小来确定评价对象的优劣等级。该法可用于人事绩效评价等方面。

层析分析法的基本步骤如下：

1. 建立指标体系及层次，构造目标图
2. 计算权重系数
3. 计算综合评分指数GI

比如我们要对几个医院的工作质量进行评价，我们将医院你的工作质量划分为三个一级子目标：膳食供应，护理工作和医疗工作三方面。一级子目标右可以划分为二级子目标：其中膳食供应由膳食质量决定；护理工作由护理制度决定；医疗工作由医疗制度、医疗质量、病床利用三方面决定。最后一层子目标有我们的统计数据得到。于是我们可以建立如下层及分析模型：

每个目标由下一级子目标构成，一个自然的问题是：下一级子目标的权重应该个分配多少？我们可以使用Saaty建议评分标准：

对于上面医院评价例子，我们假设一级子目标对总目标的判断矩阵为：

根据判断矩阵，我们计算每个元素的临时权重：
在对临时权重进行归一化，得到最终权重：

第二层子目标中，只有医疗工作被拆分成三个不同子目标，我们可以按照上面方式，计算第二层和四三层的子权重如下：

于是我们得到了每个层次中每个元素的权重（可以看做非全连接神经网络的权重W）。我们通过连乘可以得到每一个底层元素对总评价的权重：

可知，所有权重之和为1。如果我们有了几家医院的病床使用率等指标，便可以乘以对应权重后相加得到对每家医院的评价。但需要注意的是，每个底层即我们可以观察得到的指标的量纲必须是统一的。

如果我们有六家医院，使用上面层次分析结果，求得和医院评分图如下（评分本身是没意义的，只有进行比较得到排序才有意义），数据如下：

对于我们层级分析法得到的结果是否有效，可以使用判断矩阵的一致性校验，其步骤如下：

依照上面方法，对上面第一层子目标判断矩阵进行一致性校验：

得到$CR$<0.1，即认为当前层的判断矩阵是有效的。同理我们求得第二层和第三层的判断矩阵也是有效的，即认为该层次分析模型得到结果是可信的。

接下来使用python对层析分析法的核心步骤进行实现，具体的，我们对层次分析法如何求解每一层的权重，以及判断矩阵的一致性检验进行实现：

# -*- coding: utf-8 -*-
"""
Created on Mon Apr 27 10:10:24 2020

@author: nbszg
"""

import numpy as np
import pandas as pd

#对判断矩阵进行一致性检验
def CR_test(determine_mat):
    n = len(determine_mat)
    reference=np.array([0.0, 0.0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45])
    #求特征值和特征矩阵
    eigenvalue, eigenvector = np.linalg.eig(np.mat(determine_mat))
    #求最大特征值
    max_eig = eigenvalue[0]
    #计算CI
    CI = (max_eig-3)/(3-1)
    RI = reference[n-1]
    CR = CI/RI
    if CR<0.1:
        print('CR value is: {0} , results are credible\n'.format(CR))
    else:
        print('CR value is: {0} , results are not credible\n'.format(CR))
    

#计算每个子目标权重
def weight_cul(determine_mat):
    w=np.array([])
    n = len(determine_mat)
    #计算判断矩阵每一行乘积
    for i in range(n):
        w = np.append(w, pow(np.product(determine_mat[i]), 1/n))
    
    #进行归一化
    w = w/np.sum(w)
    #进行判断矩阵的一致性检验
    CR_test(determine_mat)
    
    #返回子目标权重
    return w

importance = np.array([[1,3, 5], [1/3, 1, 3], [1/5, 1/3, 1]])

w = weight_cul(importance)
print('factor weight is: {0}'.format(w))

我们使用上面例子的第一层进行计算，计算结果如下：

可以看到，程序运行的结果与前面手动计算的结果是一样的。

二、Topsis

Topsis与层析分析目标相似，都可以用户绩效评价。Topsis基本思想是：基于归一化后的原始数据矩阵，采用余弦法找出有限方案中的最优方案和最劣方案（分别用最优向量和最劣向量表示），然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。

假设我们都$n$个评价对象，每个评价对象都有$m$个指标。具体数据形式如下：

每个指标都与我们想要求得的最终绩效评价相关。其中有的指标与最终评价正相关，即指标越高，评价越高，我们称为高优指标。有的呈现负相关，即指标越高，评价越低，我们称为低优指标。还有一类指标与评价时非线性关系的，当指标未到达阈值时，为正相关，当指标超过阈值时，为负相关，我们称为中性指标。比如在做信用评价时，收入就是一个高优指标，当前在贷金额是一个低优指标，持有信用卡信用卡数我们可以认为是一个中性指标，过低（白户）或过多（大量信用卡）都倾向于信用降低。在实际应用中绝大部分指标都是高优指标或低优指标。

在Topsis中，我们需要对低优指标和中性指标做一次转化，是所有转换后的目标与我们的评价都为正相关。

接下来，还需要对指标进行归一化处理，进过归一化处理后的指标才是可以比较的。

可以求出矩阵$Z$中每一列的最大值，构成向量$Z^{+}$，每一列最小值构成向量$Z^{-}$，$Z^{+}$表示了当前数据矩阵中每个指标的最好情况，$Z^{-}$代表了最差情况。

可以根据$Z$中每一行向量与$Z^{+}$和$Z^{-}$的距离，判断每个评价对象的好坏，具体来说，一个评价对象离$Z^{+}$距离越近，离$Z^{-}$距离越远越，代表这个评价对象相对来说越好。具体评价方法如下：

与层析分析法相同，$C_i$的大小本身是没意义的，需要进行排序对比，才可一直到相对的好坏。

比如，我们对一个地区近几年的公共卫生质量进行评价，其数据如下：

根据上面的定义，数据中监督率、体检率和培训率都是高优指标，我们直接进行归一化得到$Z$矩阵：

进一步可以求出每个$Z$中每一行向量与$Z^{+}$和$Z^{-}$的距离$D^{+}$和$D^{-}$，从而得到每一年的评价$C_i$

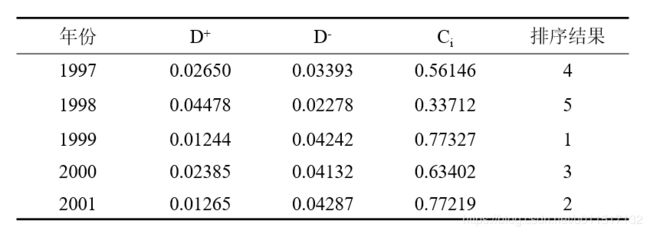
从排序结果来看，我们可以认为，1999年的公共卫生评价最好，1998年最差。

我们对上述案例进行python实现，代码如下：

# -*- coding: utf-8 -*-
"""
Created on Mon Apr 27 11:04:16 2020

@author: nbszg
"""

import numpy as np
import pandas as pd

def topsis(data, attribute):
    dmu = list(data.index)
    data = np.array(data)
    m = data.shape[0]
    n = data.shape[1]
    z_max = np.array([])
    z_min = np.array([])
    for i in range(n):
        #如果指标是低优指标
        if attribute[i] == 'bad':
            data[:,i] = 1.0/data[:,i]
        #如果指标是中性指标
        if attribute[i] == 'neutral':
            #为了简化处理，我们先将均值作为阈值，可根据实际修改
            data[:,i] = np.mean(data[:,i])/(np.mean(data[:,i])+np.abs(np.mean(data[:,i])-data[:,i]))
        
        #进行标准化
        data[:,i] = data[:,i]/(np.sqrt(np.sum(data[:,i]*data[:,i])))
        #计算每个指标最大值z_max
        z_max = np.append(z_max, max(data[:,i]))
        #计算每个指标最小值z_min
        z_min = np.append(z_min, min(data[:,i]))
    
    D_plus = np.array([])
    D_minus = np.array([])
    C = np.array([])
    for i in range(m):
        d_p = np.sqrt(np.sum((z_max-data[i,:])*(z_max-data[i,:])))
        d_m = np.sqrt(np.sum((z_min-data[i,:])*(z_min-data[i,:])))
        c = d_m/(d_p+d_m)
        D_plus = np.append(D_plus, d_p)
        D_minus = np.append(D_minus, d_m)
        C = np.append(C, c)
    
    result = pd.DataFrame()
    result['D_plus'] = D_plus
    result['D_minus'] = D_minus
    result['C'] = C
    #进行排序
    result['rank'] = result['C'].rank(ascending=False,method="first")
    result.index = dmu
    
    return result


data = pd.DataFrame()
data['监督率'] = [95.0, 100.0, 97.4, 98.4, 100.0]
data['体检率'] = [95.3, 90.0, 97.5, 98.2, 97.4]
data['培训率'] = [95.0, 90.2, 94.6, 90.3, 92.5]
data.index = ['1997', '1998', '1999', '2000', '2001']

attribute = ['good', 'good', 'good']

result = topsis(data, attribute)
print(result)

得到结果如下：

程序计算结果，与我们手动计算结果一致。

不难看出，Topsis方法认为每个指标对评价的贡献是相等的，这不一定是合理的

当我们处理问题时，可以灵活一些。本文提出一种改进方案，先使用PCA对指标进行主成分分析，然后将主成分对应特征值大小作为计算距离的权重系数，在进行距离计算，最后通过Topsis方法求得每个评价对象的评价。

三、DEA

当决策的产出可以观察时（比如决策带来的用户增长或带来的总价值），我们可以通过比较每种决策相同的投入时，产出的大小，产出越大越好。或每种决策产出向同时，投入的大小，投入越小越好。具体的我们可以建立数据包络分析模型（DEA）。这与上面层析分析和Topsis的思想和应用方式存在不同。

DEA公式和理论较多，本文直接引用网上一个比较清晰的讲解DEA (数据包络分析)介绍及 python3 实现

上面所说的CCR也称为CRS和BCC也称为VRS

上面这篇文章中利用python对DEA分析进行了实现。其中用到了gurobipy，但是gurobipy只支持学校ip，对普通用户申请不是十分友好。实际上在2017年，推出了pyDEA，其使用非常便捷，可以用过python调用，也可以直接用其与用户交互的GUI界面。具体使用方法参考Using pyDEA

我们使用与上面文章相同的数据进行试验，得到的结果如下：

可以看到计算得到每一年的TE（VRS模型结果）与OE（CRS模型结果）与文章的结果是一致的。即认为1997-1999年的综合技术效益是DEA有效的，1996-1999年的技术效益是DEA有效的。