模式识别:C-means(K-means)聚类算法与分级聚类(层次聚类)算法
C均值聚类算法与分级聚类算法的聚类分析
一、实验目的
- 理解聚类的整体思想,了解聚类的一般方法;
- 掌握 C-means与分级聚类算法算法思想及原理,并能够熟练运用这些算法进行聚类分析;
- 能够分析二者的优缺点
二、实验内容
- 采用C均值聚类算法对男女生样本数据中的身高、体重2个特征进行聚类分析,考察不同的类别初始值以及类别数对聚类结果的影响,并以友好的方式图示化结果。
- 采用分级聚类算法对男女生样本数据进行聚类分析。尝试采用身高,体重2个特征进行聚类,并以友好的方式图示化结果。
三、实验原理
3.1 C-means聚类算法
3.1.1算法原理
C-means,常称作K-means算法,是基于距离的聚类算法。采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。其基本思想:取定c 类,选取c 个初始聚类中心即 , 即代表点 。按最小距离原则将各样本分配到离代表点最近的一类中 ,不断重新计算类中心 , 调整 各样本类别,最终使聚类准则函数 Je 最小。算法采用误差平方和准则函数作为聚类准则函数。
①用样本间的距离(欧式距离)作为相似性度量
②用各类样本与类均值间的平方误差和作为聚类准则
定义准则函数:
![]() 是常用的聚类准则函数 , 表示N个样本聚类成c 类时,所产生的总误差的平方和 , 其值取决于c 个聚类中心。
是常用的聚类准则函数 , 表示N个样本聚类成c 类时,所产生的总误差的平方和 , 其值取决于c 个聚类中心。
3.1.2 C-means聚类算法流程(迭代优化)
输入:样本数据集D,聚类簇数c;输出:各类簇的集合
步骤:初始化每个簇的均值向量
repeat:
a.(更新)簇划分;
b. 计算每个簇的均值向量
until 当前均值向量均未更新
3.1.3 C-means聚类算法伪代码
输入:样本集D={x_1,x_2,...,x_n};聚类簇数c
过程:
1:从D中随机选择c个样本作为初始均值向量{u_1,u_2,...,u_c}
2:repeat
3:令C_i=Ø(1≤i≤c)
4:for j = 1,...,n do
5: 计算样本x_j与各均值向量u_i(1≤i≤c)的距离:d_ji = ||x_j-u_i||2;
6: 根据距离最近的均值向量将x_j归入该簇
7:end for
8:for i = 1,...,c do
9: 计算新的均值向量u'_i
10: if u'_i ≠ u_i then
11: 将当前均值向量u_i更新为u'_i
12: else
13: 保持当前均值向量不变
14: end if
15:end for
16:until 当前所有均值向量不再更新
17:return 簇划分结果
输出:簇划分C={C_1,C_2,...,C_c}
3.2 分级聚类算法
3.2.1算法基本原理
思想:从各类只有一个样本点开始, 逐级合并,每级只合并两类,直到最后所有样本都归到一类。聚类过程中逐级考查类间相似度,依次决定类别数。在聚类过程中把 N 个没有标签的样本分成一些合理的类时,极端情况下,最多可以分成 N 类,即每个样本为一类;最少可以分成一类,即所有样本为一类。那么可以从 N 类到 1 类逐级地进行类别划分,求得一系列类别数从多到少的划分方案,然后根据一定的指标选择中间某个适当地划分方案作为聚类结果。分级聚类树示例如图3.1
图3.1分级聚类树
树枝长度:反应节点之间的相似度或距离
距离/相似度量:如欧式距离(相似度量包括样本之间的度量与聚类之间的度量)
常用的几种类间相似度量:最近距离(single-link)、最远距离(complete-link)、均值距离(average-link)
- 单链(MIN):定义簇的邻近度为不同两个簇的两个最近的点之间的距离。
- 全链(MAX):定义簇的邻近度为不同两个簇的两个最远的点之间的距离。
- 组平均:定义簇的邻近度为取自两个不同簇的所有点对邻近度的平均值。
3.2.2 算法流程(自底向上)
a.将每个对象归为一类, 共得到N类, 每类仅包含一个对象. 类与类之间的距离就是它们所包含的对象之间的距离;
b.找到最接近的两个类并合并成一类, 于是总的类数少了一个;
c.重新计算新的类与所有旧类之间的距离;
d.重复第2步和第3步, 直到最后合并成一个类为止(此类包含了N个对象)。
四、实验平台
本实验编程运用Python语言完成。
4.1读取Excel数据应用了扩展工具包xlrd;
4.2 对于kmeans聚类算法函数的调用应用的了扩展工具包sklearn.cluster中的主函数KMeans()。其主要参数如下:
1).n_clusters:簇的个数,即你想聚成几类
2).init: 初始簇中心的获取方法。有三个可选值:’k-means++’, ‘random’,或者传递一个ndarray向量。此参数指定初始化方法,默认值为 ‘k-means++’。本实验我们使用该方法来获取初始质心。
①‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛。k-means++算法选择初始seeds的基本思想就是:初始的聚类中心之间的相互距离要尽可能的远。
算法步骤: (1)从输入的数据点集合中随机选择一个点作为第一个聚类中心 (2)对于数据集中的每一个点x,计算它与最近聚类中心(指已选择的聚类中心)的距离D(x) (3)选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大 (4)重复2和3直到k个聚类中心被选出来
(5)利用这k个初始的聚类中心来运行标准的k-means算法
②‘random’ 随机从训练数据中选取初始质心。
3).n_init: 获取初始簇中心的更迭次数,为了弥补初始质心的影响,算法默认会初始10次质心,实现算法,然后返回最好的结果。
4).max_iter: 最大迭代次数(因为kmeans算法的实现需要迭代)
4.3对于分级聚类算法函数的调用应用到了scipy.cluster中的主函数hierarchy.linkage()。或者扩展工具包sklearn.cluster中的主函数AgglomerativeClustering()。
五、实验结果
5.1 C-means聚类算法结果与分析
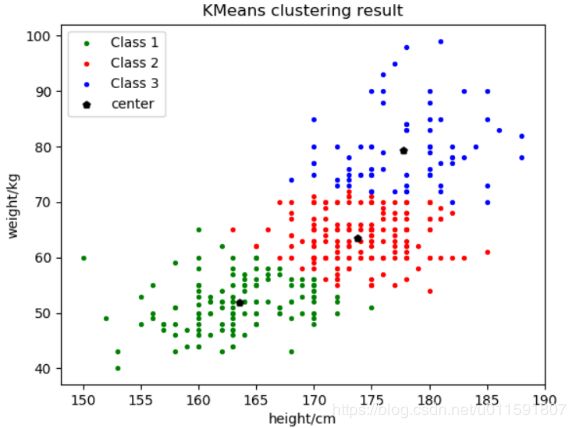
将聚类数目c分别取2,3。聚类结果如下图5-1与5-2:
图5-1聚为2类 图5-2 聚为3类
质心位置如下表:
| 聚类c |
初始质心 |
Class1质心 |
Class2质心 |
Class3质心 |
|
2类 |
k-means++ |
(175.9,70.3) |
(165.8,54.1) |
|
|
3类 |
k-means++ |
(163.4,51.4)
|
(173.2,62.9) |
(177.8,78.2) |
若开始未知类别数,画出C值与之间的关系曲线如下图5-3:
图5-3
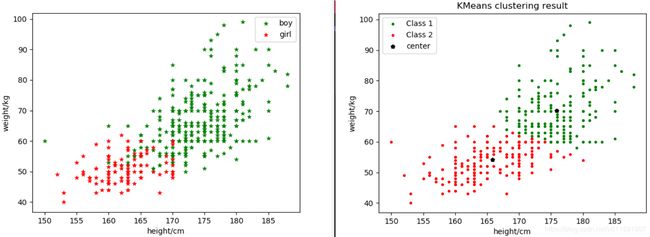
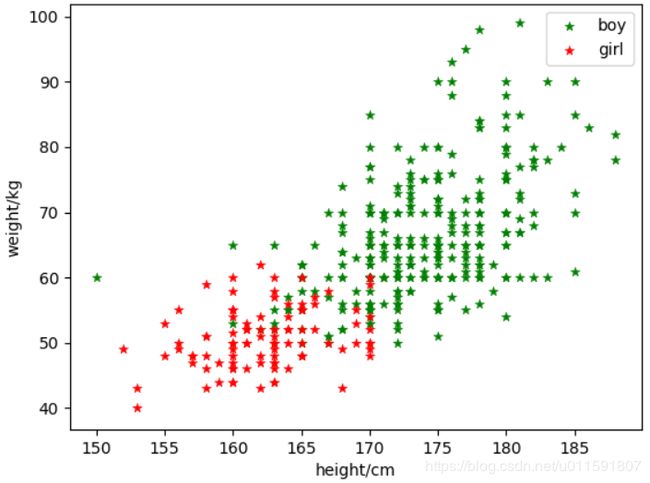
由于已知样本数据类别,故将样本散点图分布与2聚类图示做对比,如下图5-4:
图5-4
结果分析:由以上结果图示可知,该样本数据分为3类比较合理,但由于样本为性别划分,只可分为两类。由2聚类结果图示可知,在两类分界处周围出现了很多的错误划分,主要是部分男生跟女生划为一类。这些错误划分的样本数据,都体现出了体重较轻的情况(身高始终或者较矮),而这些特点与女生的体重特征相符,所以才可能导致错误的划分。这同时也说明,在做聚类时,特征的选取非常重要。
5.2分级聚类结果与分析
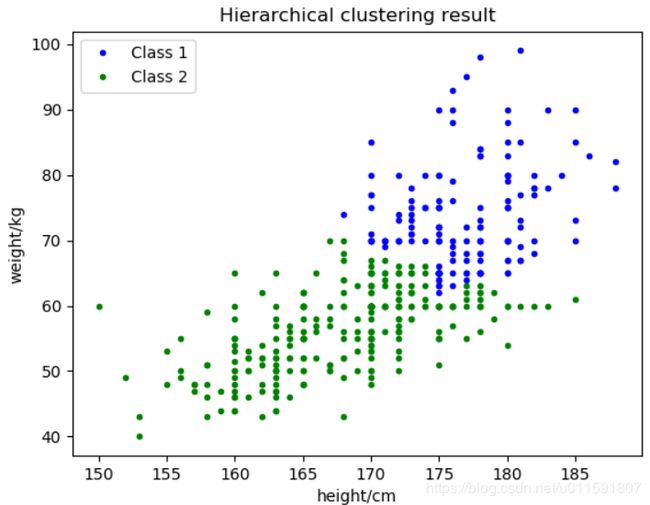
将聚类数目c分别取2,3。聚类结果如下图5-5与5-6:
图5-5聚为2类 图5-6聚为3类
样本分级聚类枝状图如下图5-7与5-8,分别采用不同的相似度量:
图5-7分级聚类枝状图(相似度量complete)
图5-8分级聚类枝状图(相似度量ward)
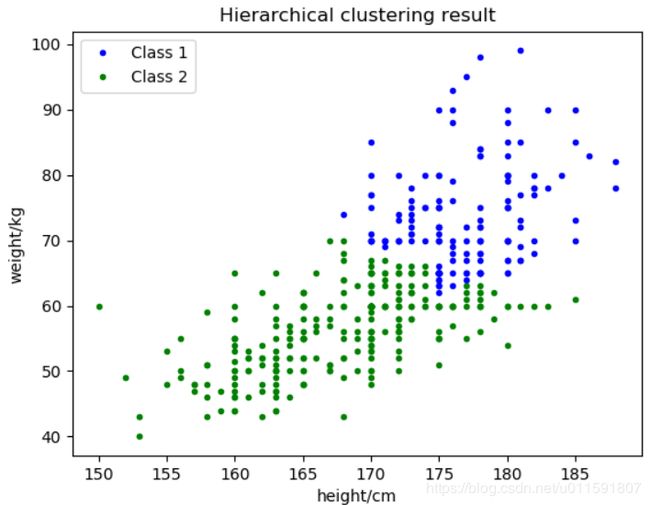
由于已知样本数据类别,故将样本散点图分布与2聚类图示做对比,如下图5-9:
图5-9
结果分析:对于同一样本集,聚为几类并不会影响分级树的形状和聚类效果,只需要在不同的级数水平画分界线就可得到分类情况。由图5-1与5-5对比可知二两聚类算法得到的二分聚类结果很相似,没有太大差别,都出现将部分男生错分为女生的现象。层次聚类判断相似度的方法在很大程度上会影响聚类的结果,因为可以看出分级聚类枝状图明显有所不同。
从实验结果来看,分级聚类的关键是:选取的特征是否能够完整地表征样本的信息与如何选择相似性度量。
5.2两者的优缺点
|
|
优点 |
缺点 |
|
Kmeans |
(1)算法快速、简单; (2)对大数据集有较高的效率并且是可伸缩性的; (3)时间复杂度近于线性,而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(nkt) ,其中n代表数据集中对象的数量,t代表着算法迭代的次数,k代表着簇的数目; (4)当结果簇是密集的,簇与簇之间区别明显时,它的效果较好。
|
(1)在 K-means 算法中 K 是事先给定的,这个 K 值的选定是非常难以估计的。有的算法是通过类的自动合并和分裂,得到较为合理的类型数目 K,例如 ISODATA 算法; (2)初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果; (3)它对于“噪声”与孤立的点样本是很敏感的,少量的该类样本对数据d的平均值产生很大的影响。 |
|
|
优点 |
缺点 |
|
分级聚类 |
(1)层次聚类最主要的优点是集群不再需要假设为类球形。另外其也可以扩展到大数据集; (2)对于K-means不能解决的非球形族就可以解决了; (3)可解释性好。
|
(1)缺点是已做的分裂操作不能撤销,类之间不能交换对象。如果在某步没有选择好分裂点,可能会导致低质量的聚类结果。大数据集不太适用; (2)时间复杂度高,o(m^3),改进后的算法也有o(m^2lgm),m为点的个数;为贪心算法,对当前获得最优,一旦出错将无法纠正; |
六、实验心得
通过本次实验,深入了解了kmeans聚类算法与分级聚类算法的思想与原理。同时熟练了对python的应用使用程度。也对算法的相似度如何影响聚类效果有了更直观的认识与理解。以及python中Kmeans如何获取优良初始聚类中心的‘k-means++’方法,使每次聚类结果尽可能相同。由于本次数据样本集较少,两类算法的分类结果相似,没有很大差别。还无法直观的看到两者的分类区别。也只能从时间复杂度上来分析二者的不同了。
七、完整代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2018-11-19 19:06:12
# @Author : Taylen Lee
# @Link : https://blog.csdn.net/u011591807
# @Version : 0.1
import xlrd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster import hierarchy
from itertools import cycle #python自带的迭代器模块
'''
/**************************task1**************************/
1.采用C均值聚类算法对男女生样本数据中的身高、体重2个特征进行聚类分析,
考察不同的类别初始值以及类别数对聚类结果的影响,并以友好的方式图示化结果。
/**************************task1**************************/
'''
mydata = xlrd.open_workbook('D:/program/py_code/data_2018.xls')
mysheet1 = mydata.sheet_by_name("Sheet1")
#获取行数、列数
nRows = mysheet1.nrows
nCols = mysheet1.ncols
#用于存取男生女生身高数据
man_height = []
woman_height = []
man_weight = []
woman_weight = []
height_weight = []
#获取第4,5列的内容:身高,体重
for i in range(nRows):
if i+1