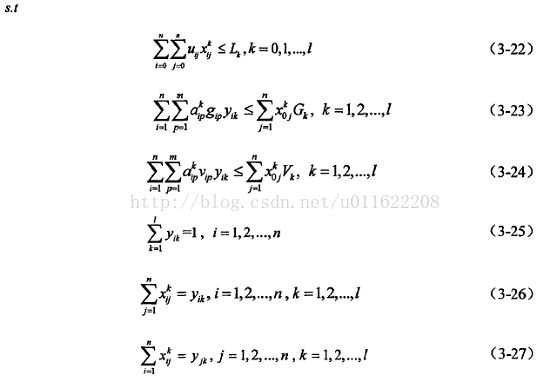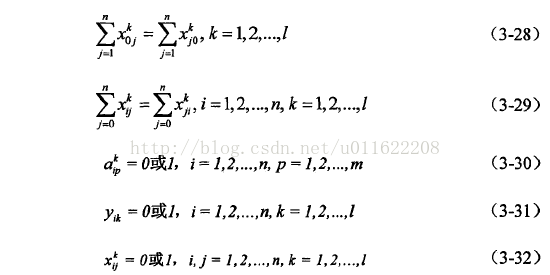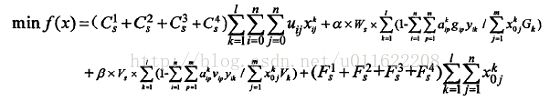遗传算法求解多约束、多类型车辆、多目标优化的车辆路径问题
目前关于车辆路径问题的模型种类很多,因此在建立综合优化模型时可选择的也很多,考虑到在实际情况中,配送中心大都是少批次、多品种的配送,需要将多个客户的货物集中到一起后再进行配送,而车辆装载货物的量有限,加之对于带载重限制的车辆路径问题的研究目前为止很多,研究背景较强,此外,结合调研中车辆有最大行驶里程限制,因此本文选择了带载重及车辆最大行驶里程限制的车辆路径模型作为综合优化的整合对象。
本文涉及到的车辆路径问题描述如下:某配送中心,共有k辆车给n个客户点进行配送,每辆车的额定载重量为Gk客户点i的货物重量为gi,车辆装载的货物总重量要小于车辆的额定载重量,使得在满足客户需求的情况下车辆总行驶路径最短。可表示如下图所示。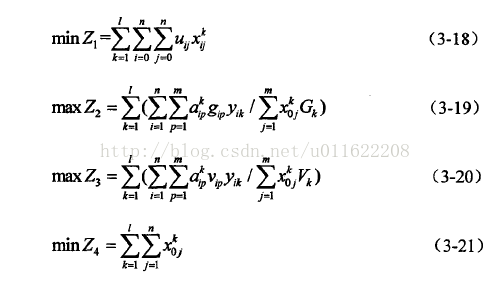
图1 车辆路径优化的模型模型
建立模型
变量太多,这里就不详细解释变量的含义,对上面4个函数解释如下:式(3-18)车辆总的行驶里程最短;式(3-19)表示车辆总载重利用率最大;式(3-20)表示车辆总容积利用率最大;式(3-21)车辆使用数量最少。
同时针对模型具有以下的约束条件:
该模型包含四个部分的目标:车辆运行里程最短,载重利用率最大,,车辆容积利用率最大,车辆使用数目最小,从优化的角度来看这是一个多目标优化的问题,所以采用通用的方法将其转化成单目标优化问题,以实现对四个目标函数的优化。
单目标转换
将上面的4个目标函数转化成以下的单目标函数:
遗传求解
设计改进的遗传算法进行求解,包括设计编码方案、初始化种群、制定解码方案、确定适应度函数、设计遗传算子、设定参数以及确定终止条件这几个步骤。
部分程序:
% Author: 怡宝2号
% Use: 基于遗传算法求解多约束条件,多类型运输车辆的车辆路径优化问题,并将4个多目标的优化问题,转化成一个单目标优化问题
% 输入变量(可修改量):
% popsize:种群大小
% T:进化代数
% 输出:
% route:运输路径
% Remark: 本人qq:778961303,如有疑问请咨询
tic;
clc;close all;clear all;%S除变量
format loose
l=20;%配送车数
vehicle=[1750 25;
2000 31.5;
2200 54;
3040 65];%不同类型车辆的载重,体积的限制
num_vehicle=[3 4 5 6]; %不同车辆的数量
limit=[]; %载重和体积的限制
for i=1:length(num_vehicle)
temp=rep(vehicle(i,:),[num_vehicle(i) 1]);
limit=[limit;temp];
end
G=limit(:,1); %车辆的载重限制
V=limit(:,2); %车辆的体积限制
N=32;%需要配送节点数
% G=1995;%^辆载重限制
% V=30;%车辆体积限制
L=250;%^辆路程限制
alpha=1;
Ws=130;%车辆满载时按载重计算的成本
Vs=140;%车辆满载时按体积计算的成本(元)
%车辆配送成本
Csl=0.3;%单位公里消耗燃料费用(元/km)
Cs2=2; %车辆折旧(元/km)
Cs3=0.03;%轮胎消耗(元/km)
Cs4=1.38;%油费(元/km)
Cs5=1.24;%养路费(元/km)
Cs6=0.15;%车辆日常维护费(元/km)
%车辆其他配送相关成本
Fsl=100;%装卸费用(元/次)
Fs2=8.9;%保险费(元/次)
Fs3=30; %文档费用(元/次)
Fs4=50; %配送材料费用(元/次)
while gen<=T
%%遗传算法选择
FitnV=ranking(Value);%分配适应度值
Chrom=select('sus',Chrom,FitnV,1);%选择
Chrom=mutationGA(Chrom,popsize,PM,N);%种群变异,单点变异
Chrom=crossGA(Chrom,popsize,PC,N);%种群交叉,两点变交叉
%%计算最优
[vl,index1]=min(Value);
gen=gen+1;
trace1(gen,1)=Value(index1);
trace1(gen,2)=mean(Value);
%%记录最优
if gen == 1
bestChrom1=Chrom(index1,:);%记录函数1的最优染色体
bestValuel=vl;%记录函数1的最优值
end
if bestValuel>vl
bestValuel = vl;%记录函数1的最优值
bestChrom1=Chrom(index1,:);
end
waitbar(gen/T,wait_hand);%每循环一次更新一次进步条
end
delete(wait_hand);%执行完后删除该进度条
%显示结果
disp(['最佳目标函数',num2str(bestValuel)]);
disp(['最佳染色体',num2str(bestChrom1)]);
disp(['总用车数量:',num2str(min(y4(:,1)))]);
%% 结果
%%转换为需要的格式和输出文件
s=bestChrom1;
needdataW=needdata(1,s);
needdataV=needdata(2,s);
route =divideroute(s,needdataW,needdataV,G,V,L,distdata);%路径划分
%求每辆车的路程,载重利用率,体积利用率
index = find(route==0);
for i = 1:length(index)-1
temp_route=route(index(i):index(i+1)); %每辆车的路径
temp_y1=objectfun_distance(temp_route,distdata); %每辆车的路程
[temp_y2 temp_y3] = pervehicle(temp_route,needdata,G(i),V(i)); %每辆车的载重、体积利用率
disp(['第' num2str(i) ' 辆车的路径:'num2str(temp_route)]);
disp(['第' num2str(i) ' 辆车行驶路程:'num2str(temp_y1)]);
disp(['第' num2str(i) '辆车的载重利用率:'num2str(temp_y2)]);
disp(['第' num2str(i) '辆车的体积利用率:'num2str(temp_y3)]);
end
disp(['传算法优化得到的最佳路径:',num2str(route)]);
disp(['遗传算法优化得到的目标函数值:',num2str(bestValuel)]);
disp(['遗传算法优化得到的总行驶里程:',num2str(min(yl(:,1)))]);
disp(['遗传算法优化得到的车辆载重未利用率',num2str(min(y2(1,:)))]);
disp(['遗传算法优化得到的车辆容积未利用率',num2str(min(y3(1,:)))]);
%% 画图
%%总目标函数
figure
plot(trace1(:,1),'b-');
hold on;
plot(trace1(:,2),'r-');
legend('目标函数最优值','目标函数均值');
xlabel('迭代次数')
ylabel('目标函数')
title('遗传算法优化成本迭代曲线')
如有疑问请咨询:qq778961303
程序运行结果: