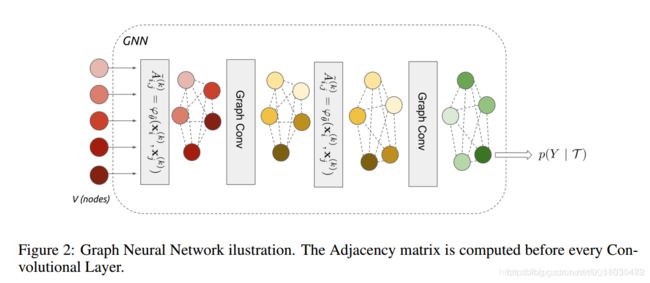
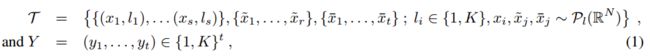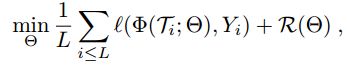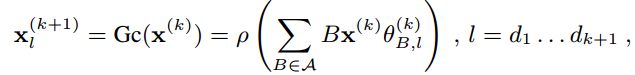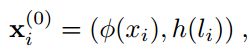论文笔记:Few-Shot Lear With Graph Neural Networks

论文链接:Few shot learning with graph neural networks

github代码链接:pytorch实现

1,INTRODUCTIION

1,元学习(新的监督学习):它的输入-输出对设置由图像集合的iid样本及其相关标签相似性代替了图像的iid样本和它相关标签.

2,探索利用相似样本的分布 代替 利用正则化取弥补数据的不足

3.文章贡献:

             1,将few-shot learning作为有监督消息传递任务,并且它用图神经网络进行端到端的训练

             2,在Omniglot和MIniImagnet 任务中,用更少的参数实现了最优的性能

             3.将这个模型扩展到半监督学习和主动学习机制中

3,problem set-up

  描述通用的设置和标注,然后把它分别应用到few-shot learning, semi-supervised ,active learning

考虑输入-输出对(Ti,Yi)i,从部分标记图像集的分布P中描述iid.

​

     其中s是已标记样本的数量, r是未标记的样本数量(r>0 用于semi-supervised 和active learning ,  t用于要分类样本的数量, k是类别数(即每个值都代表一个类别).     这篇文章只关注t=1的情况即对于每个分类任务t,只分类一个样本, :在上的特定类的图像分布.目标Yi:是没有观察到标签的指定图像的图像类别相关.(通过end-to-end训练得到的)

     给定一个训练集 ,它的有监督的学习目标是:     其中:,R是标准的正则化目标

                          ​

    Few-Shot Learning: 当 r=0,t=1,s=qK,并且集合中只有一个图像未知标签.如果每个标签(标签数为k)刚好出现q次,这叫做q-shot,K-way学习设置.

   Semi-Supervised Learning: 当r>0，t=1的时候，就变成了一个半监督学习任务了，模型根据来自于这些样本的特征分布来进行预测。

   Active Learning：在主动学习中，模型从无监督数据(未标记的样本数据)中来请求数据的标签。

4,model

   1,将输入信息映射到图像表示. 2,详细介绍这个解构. 3,该模型概括许多之前发布的few-shot模型

  Set and Graph Input Representation

  few-shot learning目的是将标签信息从有标签样本(有监督)传播到无标签query样本上.这种传播信息可以被形式化为对输入图像和标签确定的图模型的后验推理.

​

 将τ与全连接图 进行对应,其节点对应着在τ中出现的图片x(包含有标记和无标记的),没有明确固定两个图之间的相似性,它是通过参数模型判别学习相似性度量来的.

Graph Neural Networks

一个GNN层的Gc（*）操作被定义为：

​

 其中是可训练的参数，ρ为激活函数（Relu），B为节点之间的邻接矩阵。对于以上的公式近年来也生成了许多GNN变种，其中比较典型一种工作是受message-passing networks的启发，从图中当前节点的隐藏状态开学习边的特征表示

​

其中函数为参数化的对称函数，例如神经网络. 在该文中，函数被定义为多层感知机应用于两个节点向量化表示的距离。

​
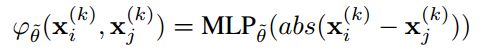
其函数的本质就是表达一个度量概念，学习两个节点向量化表示之间的绝对距离。构建出的这种距离结构具有对称性，既，。

然后，对邻接矩阵的每一行通过softmax来做归一化操作,邻接矩阵的输入集被认为有一些规则的,但这些规则不是先验的.一般来讲，网络深度的选择是根据图的大小来确定的，论文中认为深度能简单的被解释为赋予模型更强的表达能力。

Construction of Initial Node Features

模型输入样本和图中节点表示之间的映射关系可以被定义如下。

                  

Φ是一个卷积神经网络，h是样本标签的one-hot表示，两者被拼接起来。如果是未标记的样本，h被定义为一种均匀分布函数。

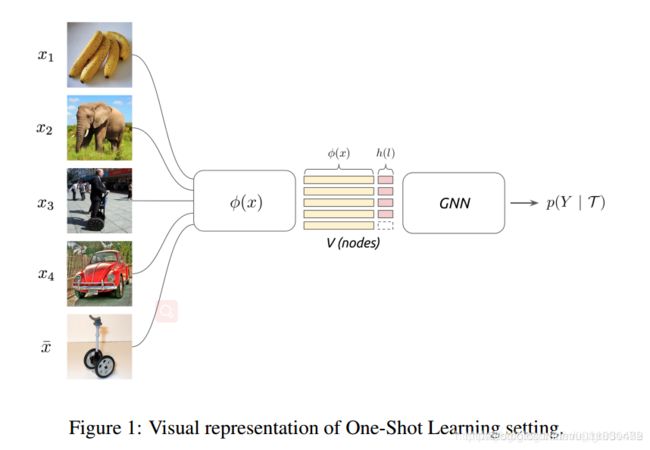
对于图二说明：在网络第一层5个样本通过边模型A～构建了图，接着通过图卷积（graph conv）获得了节点的embedding，然后在后面的几层继续用A～更新图、用graph conv更新节点embedding, 这样便构成了一个深度GNN，最后输出样本的预测标签。

在构建边模型时，先采用一个4层的CNN网络获得每个节点特征向量，然后将节点对xi,xj的差的绝对值过4层带Batch Norm和Leaky Relu的全连接层，从而获得边的embedding（1.1 A Matrix）。随后，我们将节点的embedding和边的embedding一起过图卷积网络(1.2 Gc block)，从而获得更新后的节点的embedding。（关于这段参考:https://blog.csdn.net/stund/article/details/79384485 ）

本文参考链接:https://blog.csdn.net/m0_38031488/article/details/88633511