强化学习及Python代码示例
1 概述
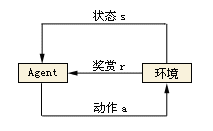
强化学习是机器学习里面的一个分支。它强调如何基于环境而行动,以取得最大化的预期收益。其灵感来源于心理学中的行为主义理论,既有机体如何在环境给予的奖励或者惩罚的刺激下,逐步形成对刺激的预期,产生能够最大利益的习惯性行为。结构简图如下:
因为强化学习考虑到了自主个体、环境、奖励等因素,所以很多人包括强化学习的研究者Richard Sutton 都认为它是人工智能中最高层的模型,其它深度学习、机器学习模型都是它的子系统。
在围棋界先后打败世界冠军的李世乭和柯洁额alphaGo就使用了强化学习模型,也正是这两次比赛,把人工智能这个概念传递给了大众。
2 结构
智能体(Agent):智能体的结构可以是一个神经网络,可以是一个简单的算法,智能体的输入通常是状态State,输出通常是策略Policy。
动作(Actions):动作空间。比如小人玩游戏,只有上下左右可移动,那Actions就是上、下、左、右。
状态(State):就是智能体的输入
奖励(Reward):进入某个状态时,能带来正奖励或者负奖励。
环境(Environment):接收action,返回state和reward。
3 思想
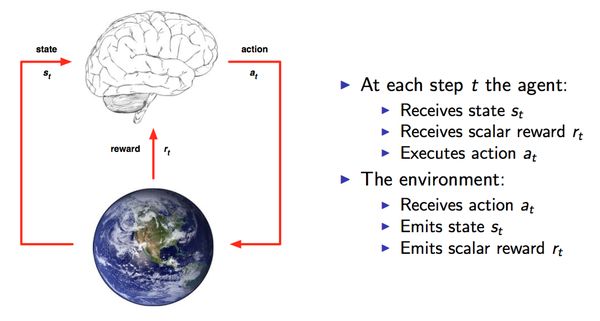
智能体对环境执行一个动作,环境接收动作后把当前状态和奖励返回给智能体;然后智能体根据环境返回的状态和奖赏执行下一个动作。
4 相关概念
探索(exploration): 不去选择最优解,而是随机选择
开发(exploitation):选择最优解
马尔科夫决策: 马尔科夫决策过程指你接下来的所有状态和决策只取决于你当前的状态和决策。比如你下象棋,你走第四步时,影响你决策和接下来状态的只有第三步。
5 执行过程
拿教电脑玩flappybird游戏来说明:
我们需要确定的两个东西是游戏,一个是电脑,
目的是电脑玩游戏。
游戏接收一个Action操作,Action是一个一维数组,比如a = [0,1] 当a[1] = 1的时候,我们让小鸟向上飞。如果是其它的数,小鸟下落。
游戏返回的是什么呢,游戏返回的是State,reward,terminal。terminal是一个布尔值True或者false,它和reward是对应的。当reward=-1时,terminal为True。reward取值有三种(1,-1,0.1)当crash时为-1,当越过障碍时为1,其它状态为0.1。而State的结构是类似80x80x4这样的图像。
也就是 currentState, reward,newState, terminal是一条数据被保存起来了。
好现在我们有了游戏的输入和输出。
看一下人的输入和输出。这里的人其实就是一个神经网络。
它是边训练,边迭代。
它的输入是state,这个有了。
但是我们还没有y啊 ,没有y我们怎么进行迭代呢。
y的计算方法是:如果停止了,y就等于本次的reward。如果这次没有停止,就等于这次的reward加上下次的价值Q
好了 有了y和x和神经网络的结构
我们的目标函数是二次函数。(y-QValue)^2。
6 推导
就是我们定义一个概念叫价值(Value),就是在某个时刻,某个状态下执行某个动作会得到一个回报(Reward),然后在下一个时刻执行某个动作又会得到一个回报,依次类推。
我们把这些回报累加起来:
![]()
这里的G相当于目前状态决策下的总回报。
如果我们把该回报的价值用一个价值函数来表示:
v(s)=E[Gt|St=s] E表示期望
即价值函数为目前状态下回报的期望。
对上式进行展开运算:
v(s)=E[Rt+1+λv(st+1|St=s)]
即得到以上贝尔曼方程。当前状态下的价值取决于当前的回报加上之后状态的价值(根据lamda决定其权重)。这其实就相当于一种动态规划的思想。
7 示例 教机器人玩Flappy bird游戏
代码地址(1):https://github.com/yenchenlin1994/DeepLearningFlappyBird
代码地址(2):https://github.com/songrotek/DRL-FlappyBird
两个不同版本都可以实现,我们拿代码1来讲述.
7.1 输入值预处理:
1)把图像大小resize成80x80
2)把图像转换成灰度图
3)把图像二值化,只有黑白两色0或者255。
4)把连续的四帧图像作为一个输入(State)。
x_t = cv2.cvtColor(cv2.resize(x_t, (80, 80)), cv2.COLOR_BGR2GRAY)
ret, x_t = cv2.threshold(x_t,1,255,cv2.THRESH_BINARY)
s_t = np.stack((x_t, x_t, x_t, x_t), axis=2)7.2 构建智能体
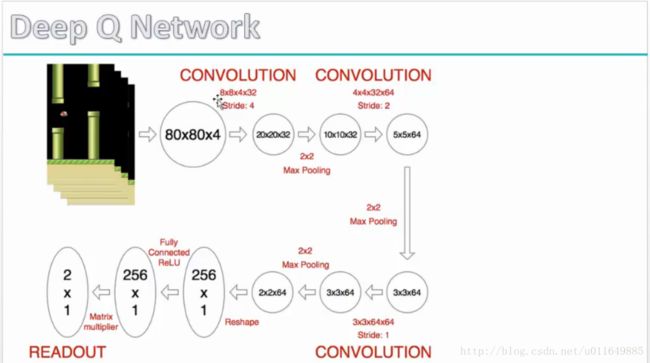
智能体是一个6层的神经网络
第一层(输入层)是80x80x4:80x80是图片的长宽像素值,4代表每次输入用4帧图片
第二层是20x20x32:20x20代表特征图的长宽,32代表特征图个数
第三层是5x5x64:5x5代表特征图的长宽,64代表特征图个数
第四层是3x3x64 -> 256x1:3x3代表特征图的长宽,64代表特征图的个数
第五层是256x1:256=2x2x64,是矩阵reshape的结果
第六层(输出层)是2x1:2代表向上走的概率和向下走的概率
注:第二层和第三层在图上都有池化,在代码中并没有这个池化操作。
然后是各层的连接方式:
第一层与第二层,第二层与第三层,第三层与第四层是卷积。
第四层与第五层,第五层与第六层是全连接。
def createNetwork():
# network weights
W_conv1 = weight_variable([8, 8, 4, 32])
b_conv1 = bias_variable([32])
W_conv2 = weight_variable([4, 4, 32, 64])
b_conv2 = bias_variable([64])
W_conv3 = weight_variable([3, 3, 64, 64])
b_conv3 = bias_variable([64])
W_fc1 = weight_variable([1600, 512])
b_fc1 = bias_variable([512])
W_fc2 = weight_variable([512, ACTIONS])
b_fc2 = bias_variable([ACTIONS])
# input layer
s = tf.placeholder("float", [None, 80, 80, 4])
# hidden layers
h_conv1 = tf.nn.relu(conv2d(s, W_conv1, 4) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2, 2) + b_conv2)
#h_pool2 = max_pool_2x2(h_conv2)
h_conv3 = tf.nn.relu(conv2d(h_conv2, W_conv3, 1) + b_conv3)
#h_pool3 = max_pool_2x2(h_conv3)
#h_pool3_flat = tf.reshape(h_pool3, [-1, 256])
h_conv3_flat = tf.reshape(h_conv3, [-1, 1600])
h_fc1 = tf.nn.relu(tf.matmul(h_conv3_flat, W_fc1) + b_fc1)
# readout layer
readout = tf.matmul(h_fc1, W_fc2) + b_fc2
return s, readout, h_fc17.3 获取智能体输入和输出
先观察100000次,把观察数据保存,然后在模型输入的时候,把这些数据拿出来作为模型的输入
# store the transition in D
D.append((s_t, a_t, r_t, s_t1, terminal))
...
s_j_batch = [d[0] for d in minibatch]
a_batch = [d[1] for d in minibatch]
r_batch = [d[2] for d in minibatch]
s_j1_batch = [d[3] for d in minibatch]
y_batch = []
readout_j1_batch = readout.eval(feed_dict = {s : s_j1_batch})
for i in range(0, len(minibatch)):
terminal = minibatch[i][4]
# if terminal, only equals reward
if terminal:
y_batch.append(r_batch[i])
else:
y_batch.append(r_batch[i] + GAMMA * np.max(readout_j1_batch[i]))7.4 迭代训练
train_step = tf.train.AdamOptimizer(1e-6).minimize(cost)7.5 智能体玩游戏
# run the selected action and observe next state and reward
x_t1_colored, r_t, terminal = game_state.frame_step(a_t)8 应用领域
可以应用到游戏控制、机器人手臂控制、推荐系统、自然语言处理上。