深度学习入门：基于Python的理论与实现 第3章 神经网络

import numpy as np
import matplotlib.pylab as plt
%matplotlib inline

阶跃函数的实现

# 只能接受实数
def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

# 接受Numpy数组
def step_function1(x):
    y = x > 0
    return y.astype(np.int)

def step_function2(x):
    return np.array(x > 0, dtype=np.int)

# 阶跃函数用到的技巧
x = np.array([-1.0, 1.0, 2.0])
print(x)
y = x > 0
print(y)
print(y.astype(np.int))

[-1.  1.  2.]
[False  True  True]
[0 1 1]

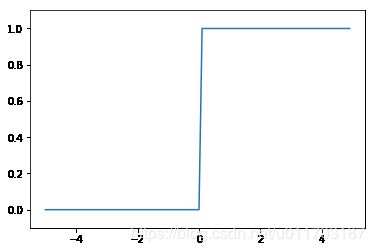
# 阶跃函数图形
x = np.arange(-5.0, 5.0, 0.1)
y = step_function2(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴范围
plt.show()

sigmoid函数

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.array([-1.0, 1.0, 2.0])
sigmoid(x)

array([0.26894142, 0.73105858, 0.88079708])

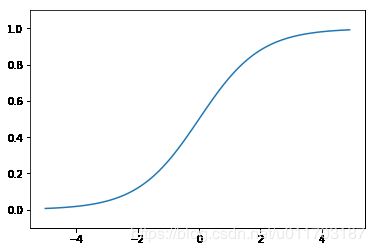
# 画sigmoid函数
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴范围
plt.show()

ReLU函数

def relu(x):
    return np.maximum(0, x)

三层神经网络的实现

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network

def identity_function(x):
    return x

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)
    
    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

[0.31682708 0.69627909]

softmax函数的实现

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

# softmax改进，防止溢出
def softmax1(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
np.sum(y)

[0.01821127 0.24519181 0.73659691]





1.0

手写数字识别

import sys, os
from mnist import load_mnist

# 第一次会花费时间比较长
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

Downloading train-images-idx3-ubyte.gz ... 
Done
Downloading train-labels-idx1-ubyte.gz ... 
Done
Downloading t10k-images-idx3-ubyte.gz ... 
Done
Downloading t10k-labels-idx1-ubyte.gz ... 
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!

print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)

(60000, 784)
(60000,)
(10000, 784)
(10000,)

# 尝试显示mnist图像
import sys, os
import numpy as np
from mnist import load_mnist
from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()
    
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5

print(img.shape) # (784,)
img = img.reshape(28, 28)
print(img.shape) # (28, 28)

img_show(img)

5
(784,)
(28, 28)

神经网络的推理处理 ch03/neuralnet_mnist.py

import sys, os
import numpy as np
import pickle
from mnist import load_mnist
from common.functions import sigmoid, softmax

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y) # 获取概率最高的元素的索引
    if p == t[i]:
        accuracy_cnt += 1
#print(network['W1'].shape)        
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

Accuracy:0.9352

神经网络的批处理的实现

import sys, os
import numpy as np
import pickle
from mnist import load_mnist
from common.functions import sigmoid, softmax

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

x, t = get_data()
network = init_network()

batch_size = 100  # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1) # 获取概率最高的元素的索引
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

Accuracy:0.9352