机器学习——多层感知机MLP的相关公式
i i i作为上一层神经元的下标,或者是输入层节点
j j j作为当前层神经元的下标,或者是隐藏层神经元
k k k作为下一层神经元的下标,或者是输出层神经元
i , j , k i,j,k i,j,k表示不同层的相对关系: i → j → k i\rightarrow j\rightarrow k i→j→k
w i j w_{ij} wij表示上一层各神经元到当前神经元的权重,也就是神经元 j j j的权重
w j k w_{jk} wjk表示当前神经元与下一层各神经元的权重,也就是神经元 k k k的权重
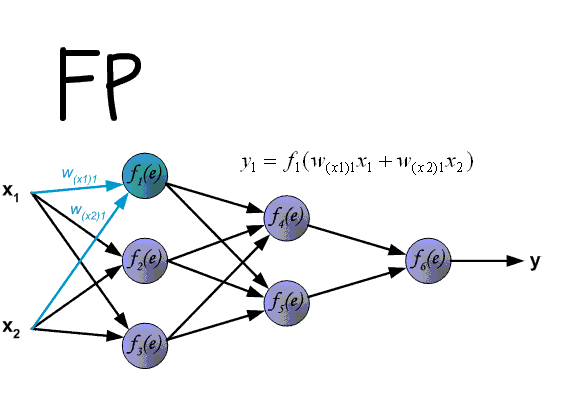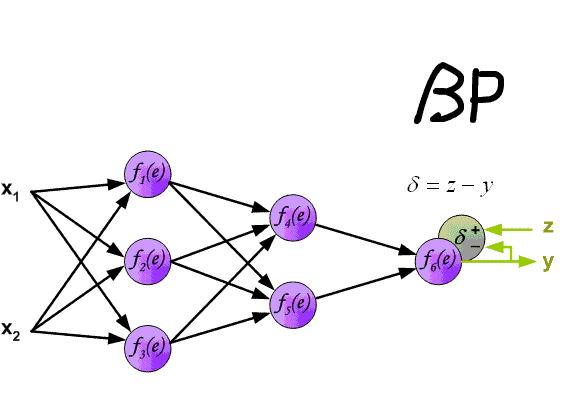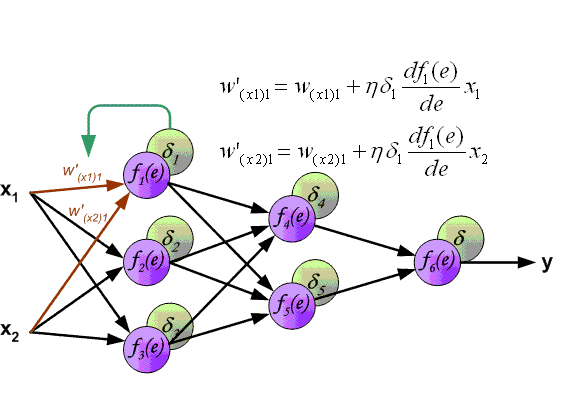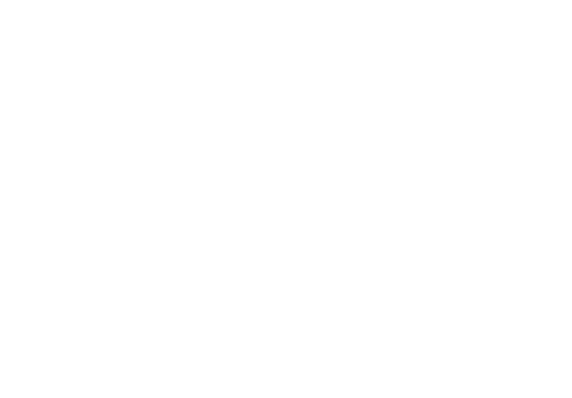
前向传播
加权求和 h h h
h j = ∑ i = 0 M w i j x j h_j=\sum_{i=0}^Mw_{ij}x_j hj=i=0∑Mwijxj
- h j h_j hj表示当前节点的所有输入加权之和
神经元输出值 a a a
a j = g ( h j ) = g ( ∑ i = 0 M w i j x i j ) a_j=g(h_j)=g(\sum_{i=0}^Mw_{ij}x_{ij}) aj=g(hj)=g(i=0∑Mwijxij)
- a j a_j aj表示隐藏层神经元的输出值
- g ( ) g() g()代表激活函数, w w w是权重, x x x是输入, w 0 j x 0 j w_{0j}x_{0j} w0jx0j表示偏移节点(bias node)
- a j = x j k a_j=x_{jk} aj=xjk,即当前层神经元的输出值,等于下一层神经元的输入值
输出层的输出值 y y y
y = a k = g ( h k ) = g ( ∑ i = 0 M w j k x j k ) y=a_k=g(h_k)=g(\sum_{i=0}^Mw_{jk}x_{jk}) y=ak=g(hk)=g(i=0∑Mwjkxjk)
- y y y表示输出层的值,也就是最终结果
- h k h_k hk表示输出层神经元 k k k的输入加权之和
激活函数 g ( h ) g(h) g(h)
采用Sigmoid function:
g ( h ) = σ ( h ) = 1 1 + e − h g(h)=\sigma(h)=\frac{1}{1+e^{-h}} g(h)=σ(h)=1+e−h1
sigmoid函数的导数:
σ ′ ( x ) = σ ( x ) [ 1 − σ ( x ) ] \sigma'(x)=\sigma(x)\left[1-\sigma(x)\right] σ′(x)=σ(x)[1−σ(x)]
将 a j = g ( h j ) a_j=g(h_j) aj=g(hj)代入可得
g ′ ( h ) = a j ( 1 − a j ) g'(h)=a_j(1-a_j) g′(h)=aj(1−aj)
损失函数 E E E
采用简单的误差平方和(sum-of-squares error function)
E = 1 2 ∑ k = 1 N ( y − t ) 2 E=\frac 1 2 \sum_{k=1}^N(y-t)^2 E=21k=1∑N(y−t)2
- 平方是为了避免超平面两端的误差点相互抵消( y − t y-t y−t存在正负)
- 前面系数取 1 2 \frac1 2 21是为了之后采用梯度下降时,求梯度(偏导数)时能抵消平方求导后的2
误差反向传播——更新权重
采用梯度下降求最优解,也就是求损失函数 E E E关于权重 w w w的偏导数
∂ E ∂ w i k = ∂ E ∂ h k ∂ h k ∂ w i k \frac{\partial E}{\partial w_{ik}}=\frac{\partial E}{\partial h_k}\frac{\partial h_k}{\partial w_{ik}} ∂wik∂E=∂hk∂E∂wik∂hk等式右边可以解释为:如果我们想知道当权重 w w w改变时,输出的误差 E E E是如何变化的,我们可以通过观察误差 E E E是如何随着激活函数的输入值 h h h变化,以及激活函数的输入值 h h h是如何随着权重 w w w变化
- h k h_k hk表示输出层神经元 k k k的所有输入加权之和,也就是激活函数 g ( h ) g(h) g(h)的输入值
右边第二项最终可以推导出下面公式,也就是上一层神经元的输出值
∂ h k ∂ w j k = a j \frac{\partial h_k}{\partial w_{jk}}=a_j ∂wjk∂hk=aj
输出层增量项 δ o \delta_o δo
右边第一项比较重要,这里称为增量项 δ \delta δ(error or delta term),继续通过链式法则推导,最终得到输出层的增量项 δ o ( k ) = ∂ E ∂ h k = ∂ E ∂ y ∂ y ∂ h k = ( y − t ) g ′ ( h k ) \delta_o(k)=\frac{\partial E}{\partial h_k}=\frac{\partial E}{\partial y}\frac{\partial y}{\partial h_k}=(y-t)g'(h_k) δo(k)=∂hk∂E=∂y∂E∂hk∂y=(y−t)g′(hk)
接下来可以对输出层的权重 w w w进行更新
更新输出层权重 w j k w_{jk} wjk
对损失函数使用梯度下降法,更新权重:
w j k ← w j k − η ∂ E ∂ w j k w_{jk}\leftarrow w_{jk}-\eta \frac{\partial E}{\partial w_{jk}} wjk←wjk−η∂wjk∂E
于是得到 w j k = w j k − η δ o ( k ) a i w_{jk}=w_{jk}-\eta \delta_o(k)a_i wjk=wjk−ηδo(k)ai
- a i a_i ai是上一层的输出值,也即是输出层的输入值 x i x_i xi
更新隐藏层增量项 δ h \delta_h δh
δ h ( j ) = g ′ ( h j ) ( ∑ k = 1 N δ o ( k ) w j k ) \delta_h(j)=g'(h_{j})(\sum_{k=1}^N\delta_o(k)w_{jk}) δh(j)=g′(hj)(k=1∑Nδo(k)wjk)
- w j k w_{jk} wjk是当前隐藏层神经元 j j j与输出层神经元 k k k之间的权重
更新隐藏层权重 v j ( 即 w i j ) v_j(即w_{ij}) vj(即wij)
v j = v j − η a j ( 1 − a j ) ( ∑ k = 1 N δ o ( k ) w j k ) a i v_j=v_j-\eta a_j(1-a_j)(\sum_{k=1}^N\delta_o(k)w_{jk})a_i vj=vj−ηaj(1−aj)(k=1∑Nδo(k)wjk)ai
- a j a_j aj是当前神经元的输出值, a j = g ( h j ) a_j=g(h_j) aj=g(hj)
- a i a_i ai是当前层神经元的输入值(也就是上一层的输出值), ∑ a i j w i j = h j \sum a_{ij}w_{ij}=h_j ∑aijwij=hj
当有隐藏层有多层时
v j = v j − η a j ( 1 − a j ) ( ∑ k = 1 N δ h ( k ) w j k ) a i v_j=v_j-\eta a_j(1-a_j)(\sum_{k=1}^N\delta_h(k)w_{jk})a_i vj=vj−ηaj(1−aj)(k=1∑Nδh(k)wjk)ai
- 公式几乎不变:
- δ o \delta_o δo变为 δ h \delta_h δh;
- k k k从表示输出层,变成表示隐藏层 j j j的下一层